Учебное пособие по дисциплине Теория автоматического управления для студентов направлений
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
Рисунок 3.1 - Схема замены двух последовательных звеньев эквивалентным звеном:а) –исходная схема; б) –после преобразования3.2.2 Два параллельных звена могут быть заменены эквивалентным звеном с передаточной функцией, равной сумме передаточных функций этих звеньев (рисунок 3.2). 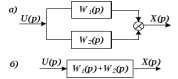 Рисунок 3.2 - Схема замены двух последовательных звеньев эквивалентным звеном: а) –исходная схема; б) –после преобразования 3.2.3 Звено, охваченное обратной связью с передаточной функцией Woc (рисунок 3.3), может быть заменено в схеме эквивалентным звеном с передаточной функцией: 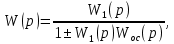 (3.1) (3.1)где W1(p)– передаточная функция звена, охваченного обратной связью. Плюс в знаменателе соответствует отрицательной обратной связи, минус –положительной.  Рисунок 3.3 - Параллельно-встречное соединение звеньев или соединение с обратной связью 3.2.4 Перенос сумматора может быть выполнен по ходу движения сигнала (рисунок 3.4) с добавлением элемента, через который переносится сумматор. 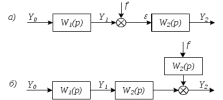 Рисунок 3.4 - Перенос сумматора по ходу движения сигнала: а) исходная схема; б) после преобразования 3.2.5 Перенос сумматора против хода движения сигнала (рисунок 3.5) выполняется с добавлением элемента 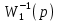 . .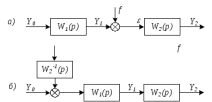 Рисунок 3.5 - Перенос сумматора против хода движения сигнала: а) исходная схема; б) после преобразования 3.2.6 Перенос узла по ходу движения сигнала (рисунок 3.6) выполняется с добавлением элемента 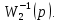 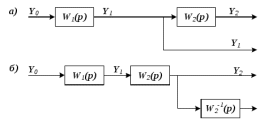 Рисунок 3.6 - Перенос узла по ходу движения сигнала: а) исходная схема; б) после преобразования 3.2.7 Перенос узла против хода движения сигнала (рисунок 3.7) выполняется с добавлением элемента W1(s). 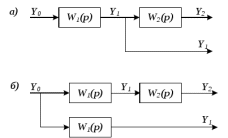 Рисунок 3.7 - Перенос узлапротив хода движения сигнала: а) –исходная схема; б) –после преобразования 3.2.8 Только узлы и только сумматоры можно переставлять местами, не добавляя звеньев (рисунок 3.8.). 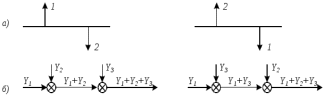 Рисунок 3.8 - Перенос узлов (а) и сумматоров (б) 3.3 Вычисление передаточной функции в одноконтурной системе Замкнутую систему называют одноконтурной, если при размыкании в какой-либо точке получается цепь из последовательно соединенных звеньев, т.е. не содержащая параллельных и обратных связей. Участок от входного воздействия до точки съема выходного сигнала называется прямой цепью. Цепь, состоящая из последовательных звеньев замкнутого контура после размыкания цепи обратной связи, называется разомкнутой цепью (рисунок 3.9).  Рисунок 3.9 - Структурная схема САР: g –входная переменная (управляющее или возмущающее воздействие); у –выходная переменная (вектор состояния, выходной параметр); W0W1W2 –прямая цепь; W1W2W3 –разомкнутая цепь Передаточная функция одноконтурной системы равна дроби, числитель которой равен произведению передаточных функций звеньев прямой цепи, знаменатель единица плюс (минус) передаточная функция разомкнутой цепи (плюс соответствует отрицательной обратной связи, минус –положительной): 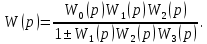 (3.2) (3.2)3.4 Построение передаточной функции многоконтурной системы Система, в которой после размыкания какой-либо из обратных связей, остаются другие обратные связи, называется многоконтурной. В многоконтурных системах сначала избавляются от локальных обратных связей и локальных параллельно-согласных соединений, последовательно применяя три простейших правила, чтобы получить систему одноконтурную. 3.5 Многоконтурные системы с перекрещивающимися обратными связями В многоконтурной системе контур обратной связи может охватывать такой участок цепи, который содержит только начало или конец другой обратной связи, такие обратные связи называют перекрещивающимися. Схемы такого типа для проведения расчетов преобразуются в схемы без перекрещивающихся обратных связей путем переноса сумматоров и узлов. Затем участки с локальными (местными) обратными связями заменяются звеньями с соответствующими передаточными функциями, система становится одноконтурной. Пример 3.1. Для системы (рисунок 3.10) многоконтурной с перекрещивающимися обратными связями записать передаточную функцию. 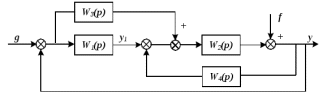 Рисунок 3.10 - Многоконтурная система с перекрещивающимися обратными связями Структурная схема преобразуется переносом сумматоров в многоконтурную без перекрещивающихся обратных связей (рисунок 3.11). 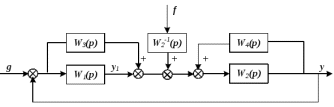 Рисунок 3.11 - Многоконтурная система без перекрещивающихся обратных связей Рисунок 3.11 - Многоконтурная система без перекрещивающихся обратных связейУчастки структурной схемы с локальными обратными связями можно заменить эквивалентными с передаточными функциями: 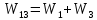 , ,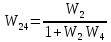 , ,что позволяет получить одноконтурную систему (рисунок 3.12). 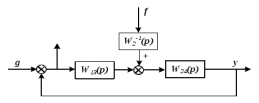 Рисунок 3.12 - Одноконтурная система (после преобразования) 3.6 Построение передаточных функций для систем с несколькими входами и выходами Передаточные функции для системы, имеющей несколько входов и несколько выходов, строятся по каждому входу и выходу в отдельности, при рассмотрении реакции на выбранное воздействие все остальные воздействия считаются равными нулю (принцип суперпозиции для линейных систем); передаточные функции образуют матрицу передаточных функций. В рассматриваемом примере по входу g(t) можно построить две передаточные функции: первая, если за отклик считать выходную величину y(t), вторая- если откликом считать разность между g(t) и y(t), т.е. отклонение ɛ(t): 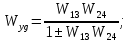 (3.3) (3.3)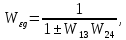 (3.4) (3.4)при этом f(t) считается равной нулю (f(t)=0). Для определения передаточной функции по входу f(t) (g(t)=0) необходимо для наглядности перестроить структурную схему (рисунок 3.13). Тогда относительно возмущения f(t) передаточные функции имеют вид: 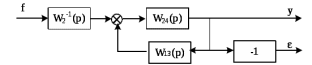 Рисунок 3.13 - Структурная схема относительно возмущающего воздействия f(t) Матрица передаточных функций f(t) передаточные функции имеют вид: 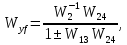 (3.5) (3.5)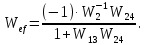 (3.6) (3.6)Матрица передаточных функций (передаточных отношений) имеет вид: 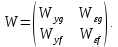 (3.7) (3.7)3.7 Построение передаточных функций в многосвязных системах Системы регулирования бывают многосвязными, т.е. выходная характеристика одной подсистемы подается на вход другой подсистемы (рисунок 3.14).  Рисунок 3.14- Структурная схема многосвязной системы Для построения передаточной функции таких систем нужно построить передаточные функции, считая при построении передаточной функции по выбранному входу и выходу остальные входы и выходы равными нулю: 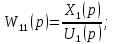 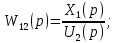 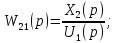 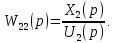 3.8 Построение передаточных функций сложных систем в пакете Matlab 3.8.1 Построение передаточных функций Для написания передаточной функции можно использовать два способа. Если передаточная функция задана в виде алгебраической дроби, числитель и знаменатель которой представляют собой многочлены вида: 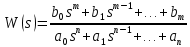 , (3.8) , (3.8)то используется синтаксис: название системы=tf([коэффициенты числителя],[коэффициенты знаменателя]). Пример 3.2. Записать передаточную функцию системы: 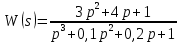 . .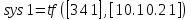 Передаточную функцию можно записать с помощью нулей и полюсов числителя и знаменателя. Пример 3.3. Записать передаточную функцию системы в пакете Matlab. 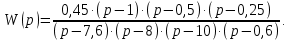 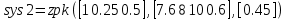 3.8.2 Соединение элементов Если два звена соединены последовательно, то их передаточная функция находится командой series. Пример 3.4. Даны передаточные функции двух звеньев, соединенных последовательно. Найти передаточную функцию такой системы, если 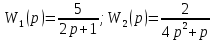 . .Задаются передаточные функции элементов: 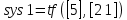 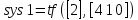 Передаточная функция при последовательном соединении этих элементов: 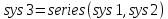 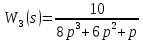 . .Если два звена соединены параллельно, то для получения передаточной функции используется команда parallel. Пример 5. Если заданы две системы в командной строке пакета Matlab, например, sys1 и sys2, то, чтобы найти передаточную функцию, нужно ввести команду: 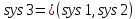 . .Замечание. Программа воспринимает в команде не более двух звеньев сразу, при большем числе элементов необходимо либо выполнять соединения последовательно несколько раз, либо воспользоваться вложенными командами: 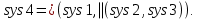 При соединении с обратной связью используется команда feedback, в скобках указывается с начала элемент, охваченный обратной связью, и через запятую элемент цепи обратной связи. Например, для рисунка 3.15 эквивалентная передаточная функция (sys3) находится следующим образом: 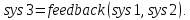 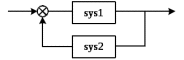 Рисунок 3.15 - Пример соединения с обратной связью Если обратная связь единичная, то 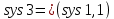 . . 3.9Задания для самостоятельной работы 3.9.1 Построить передаточную функцию регулятора скорости по управлениюg и по воздействию Mн (рисунок 3.16) разомкнутой и замкнутой системы, а также по ошибке. 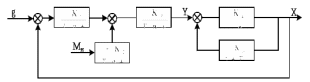 Рисунок 3.16 - Структурная схема к заданию 3.9.1 3.9.2 Найти передаточные функции замкнутой системы (рисунок 3.17) Wxg; Wyg. 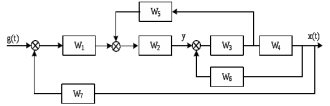 Рисунок 3.17 - Структурная схема к заданию 3.9.2 3.9.3 Построить передаточные функции двухсвязной системы (рисунок 3.18). 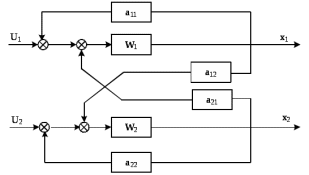 Рисунок 3.18 - Структурная схема к заданию 3.9.3 3.10Контрольные вопросы Что такое передаточная функция? Принцип суперпозиции в линейных системах. Три простейших способа соединения элементов и расчета эквивалентных функций. Одноконтурные и многоконтурные системы, расчет их эквивалентных передаточных функций. Алгоритм вычисления передаточных функций в многоконтурных системах. Вычисление передаточных функций в многоконтурных системах. 7) Когда передаточная функция прямой цепи и разомкнутой имеют одинаковое выражение? 8) Какие команды в программе Matlab используются при последовательном соединении, при параллельно-согласном, при соединении с обратной связью? 9) Как в программе Matlab можно выполнить соединение более двух элементов? 4 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ НА ТЕМУ «ПРЕОБРАЗОВАНИЕ СПОСОБОВ СОЕДИНЕНИЯ ЭЛЕМЕНТОВ В СТРУКТУРНОЙ СХЕМЕ» Цель практического занятия: научиться преобразованию одного способа соединения (последовательного, параллельно-согласного, соединения с обратной связью) в другой эквивалентный способ соединения. 4.1 Основные сведения и определения Элементы структурных схем могут соединяться тремя принципиально разными способами. 4.1.1 При последовательном соединении выходной сигнал предыдущего элемента x1(t) (реакция на входной сигнал u(t)) передается полностью на вход последующего элемента (рисунок 4.1) с выходной характеристикой x(t). 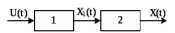 Рисунок 4.1 – Последовательное соединение элементов 1 и 2 Введение изображений сигналов позволяет использовать понятие передаточной функции элементов 1 и 2, тогда эквивалентная передаточная функция рассчитывается следующим образом:     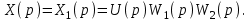 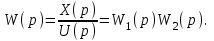 (4.1) (4.1)Правило 1. При последовательном соединении элементов их передаточные функции перемножаются. 4.1.2 При параллельно – согласном включении элементов 1 и 2 входной сигнал u(t) подается на вход обоих элементов, реакции x1(t) и x2(t) потом складываются на сумматоре 3 (рисунок 4.2), результат сложения таким образом представляет выходную характеристику x(t). 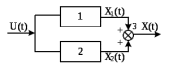 Рисунок 4.2 – Параллельно – согласное соединение элементов 1 и 2 После перехода к изображениям 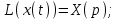 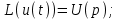 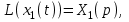 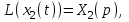 изображение выходного сигнала складывается из изображений 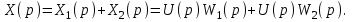 Тогда передаточная функция W(s) системы, приведенной на рисунке 4.2, имеет вид:  (4.2) (4.2)Правило 2. При параллельно – согласном соединении элементов их передаточные функции складываются. 4.1.3 Параллельно – встречным соединением или соединением с обратной связью называется такое соединение, когда сигнал с выхода первого элемента x(t) подается полностью или после преобразования вторым элементом (u2(t)) обратно на вход первого элемента со знаком плюс или минус, изменяя тем самым входное воздействие u(t) (рисунок 4.3).  Рисунок 4.3 – Параллельно – встречное соединение Операторные уравнения в изображении по Лапласу, описывающие движение сигналов, имеют вид:   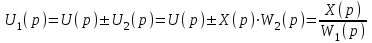 , ,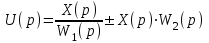 . .Знак плюс соответствует положительной обратной связи, минус – отрицательной. После простых алгебраических преобразований получается передаточная функция W(p) системы, приведенной на рисунке 3: 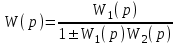 , (4.3) , (4.3)где знак плюс соответствует отрицательной обратной связи, знак минус – положительной. |
