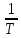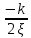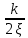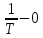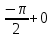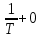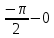Учебное пособие по дисциплине Теория автоматического управления для студентов направлений
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
1.2 Основные определения в системах автоматического управления В системах автоматического управления присутствуют все общие свойства систем. Так в соответствии со свойством иерархичности в структуре автоматических систем управления (САУ) выделяют два функциональных качественно различных элемента той или иной сложности: объект управления и устройство управления. Объект управления – совокупность технических устройств, обеспечивающих выполнение рабочих операций. Устройство управления – средства автоматизации, обеспечивают замену труда человека в операциях управления. В теории автоматического управления рассматривается взаимодействие этих подсистем с точки зрения изменения характеристик (параметров) технологических процессов (объект управления) под влиянием тех или иных управляющих воздействий. Структурная схема представлена на рисунке 1.1. Устройство управления (УУ) преобразует входное воздействие x(t) в управляющее воздействие u(t) тем или иным способом. Это преобразование называется законом управления. Законы управления могут иметь достаточно сложную форму, однако существуют несколько достаточно простых, их называют примитивными законами. Это пропорциональный, интегральный и дифференциальный законы и их комбинации. 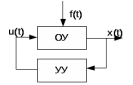 Рисунок 1.1 – Структурная схема САУ: ОУ – объект управления; УУ – устройство управления; x(t) – вектор состояния; f(t) – вектор возмущения; u(t) – вектор управления По способу учета влияния возмущающих воздействий, которые могут быть контролируемые и неконтролируемые, системы подразделяются по принципам управления. Их три: разомкнутое управление (рисунок 1.2), управление с компенсацией возмущающего воздействия (рисунок 1.3) и принцип обратной связи (рисунок 1.4). 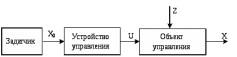 Рисунок 1.2 – Структурная схема, использующая принцип разомкнутого управления 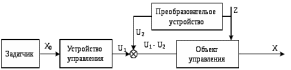 Рисунок 1.3 – Принцип управления с компенсацией возмущающего воздействия 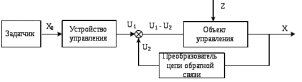 Рисунок1.4 – Принцип управления с обратной связью САУ как система должна иметь цель, т.е. вектор состояния должен иметь определенное значение, независимо от возмущающих воздействий. Системы управления по характеру вектора состояния (по цели) можно классифицировать как системы стабилизации (вектор состояния имеет постоянное значение), системы с программным управлением (вектор состояния изменяется по определенному закону), системы с поиском экстремума, системы оптимального управления. Системы автоматического управления можно классифицировать по сложности структуры. Критерием в этом случае является наличие обратных связей. Соединение называется соединением с обратной связью, если часть сигнала или весь сигнал с выхода подается обратно на вход, если со знаком плюс, то обратная связь называется положительной, если со знаком минус, то отрицательной. Обратная связь, охватывающая часть элементов, называется местной или локальной, если охватываются все элементы, то обратную связь называют глобальной. По этому признаку различают одноконтурные и многоконтурные системы. Если после обрыва какой-либо обратной связи в структурной схеме остаются другие обратные связи, то система считается многоконтурной. По степени определенности сигналов системы подразделяются на детерминированные и стохастические (вероятностные, случайные, неопределенные). По характеру сигналов во времени системы подразделяются на непрерывные и дискретные. Два последних признака являются важными при выборе математических приемов в процессе построения модели системы. Так при исследовании свойств непрерывных детерминированных систем используется классическое дифференциальное и интегральное исчисление, для стохастических непрерывных систем применяется теория случайных функций, теория вероятностей подходит для дискретных стохастических систем, а булева алгебра может быть применена к исследованию детерминированных дискретных систем. Математическая модель позволяет исследовать свойства системы, такие как устойчивость и качество управления. Основанием для получения математической модели являются объективные природные закономерности (физические, химические и другие законы). При построении математической модели используются ряд приемов: декомпозиция, линеаризация и упрощение. При декомпозиции в сложном объекте выделяются отдельные составляющие, в которых можно определить причинно-следственную связь, на ее основании строятся модели отдельных блоков, а затем их объединяют в модель исходного объекта. При линеаризации используются ряды Тейлора, в которых исключаются все нелинейные слагаемые с учетом их малости. В случае применения такого приема, как упрощение, проводится сравнение малых величин по порядку их малости, при этом исключаются все малые более высокого порядка малости. Применение этих приемов возможно, если при построении моделей используются не абсолютные значения переменных, а их относительные изменения, определенные относительно некоторого базового или номинального значения. При использовании приведенных выше приемов получается математическая модель первого приближения, линейная относительно векторов воздействия и состояния. Если результаты расчетов вектора состояния по линейной модели значительно отличаются от фактических значений, то такая модель не является адекватной процессу, поэтому необходимо вернуться на стадию получения модели. Система, имеющая математическое описание в форме линейного неоднородного дифференциального уравнения с постоянными коэффициентами, называется линейной непрерывной детерминированной системой, и дифференциальное уравнение является одной из форм математической модели таких систем. Математические модели линейных систем могут быть представлены в форме операторных уравнений, передаточных функций, частотных характеристик, временных характеристик, определения которых и алгоритмы получения рассмотрены в примере 1.1. Пример 1.1. Построение модели регулятора скорости Уатта. Решение: Данный регулятор (рисунок 1.5) относится к регуляторам непрямого действия. 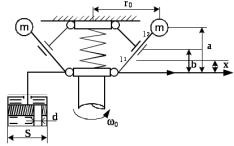 Рисунок 1.5 – Схема регулятора скорости Уатта При увеличении скорости вращения вала под действием центробежной силы радиус разлета грузиков кулисного механизма увеличивается, вся система вместе с валом вращения начинает движение вверх. Этому противодействует пружина, которая при этом сжимается. Также вверх движется и поршень в цилиндре, заполненном вязкой жидкостью. Из-за несжимаемости жидкости давление над поршнем становится больше, чем под поршнем, тогда через отверстие небольшого диаметра жидкость начинает перетекать сверху вниз, сглаживая колебания пружины. Перемещение управляющего органа х уменьшает подачу агента, вызывающего вращение вала, и его скорость становится меньше. Таким образом, движущей силой (входным воздействием) является изменение скорости вращения вала. Система окажется в равновесии, когда изменение центробежной силы будет уравновешиваться силой противодействия пружины, ньютоновой силой (система из состояния покоя начинает движение, т.е. есть с ускорением) и силой демпфирования за счет перетока жидкости через отверстие в поршне. Формула центробежной силы имеет вид (1.1): 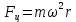 ; (1.1) ; (1.1)При расчете изменения величины центробежной силы учитываются особенности кулисного механизма, тогда используется формула центробежной силы (1.2); 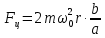 . (1.2) . (1.2)Приращение центробежной силы рассчитывается по формуле (1.2): 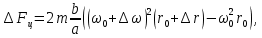 здесь множитель 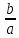 обеспечивает учет особенностей кулисного механизма. обеспечивает учет особенностей кулисного механизма.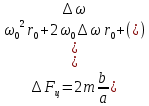 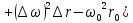 = == 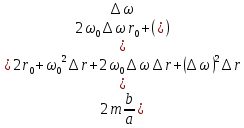 При сравнении бесконечно малых отбрасываются слагаемые, имеющие по сравнению с линейными меньшие значения. Тогда приращение центробежной силы в первом приближении имеет вид: 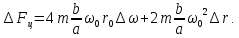 Сила противодействия пружины зависит от величины перемещения х(1.3): 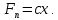 (1.3) (1.3)Ньютонова сила рассчитывается по формуле (1.4): 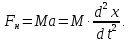 (1.4) (1.4)Сила демпфирования прямо пропорциональна площади поршня, обратно пропорциональна диаметру отверстия в поршне. Чем более вязкая жидкость находится в цилиндре, тем медленнее будет процесс выравнивания давления, чем выше скорость перемещения поршня, тем больше сопротивление этому, поэтому формула демпфирующей силы имеет вид (1.5): 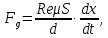 (1.5) (1.5)где Re- число Рейнольдса, учитывающее характер движения жидкости (ламинарный или турбулентный). Таким образом, уравнение равновесия имеет вид: 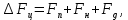 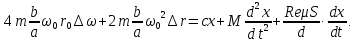 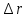 можно выразить через перемещение регулирующего органа х с учетом плеч кулисного механизма, можно выразить через перемещение регулирующего органа х с учетом плеч кулисного механизма, 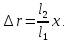 При построении моделей принято слева помещать результаты процесса (состояние), а справа записывать воздействия: 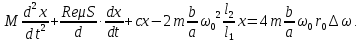 Еще одним требованием при построении модели является единичный коэффициент при переменной состояния, поэтому в полученном выражении необходимо разделить левую и правую часть на 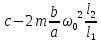 : :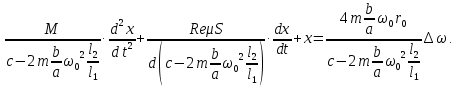 Коэффициент при второй производной по требованию анализа размерностей должен иметь смысл постоянной времени во второй степени, при первой производной – просто постоянной времени, а физический смысл коэффициента при управляющем воздействии сводится к усилению или ослаблении этого влияния, т.е. является коэффициентом передачи. 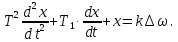 (1.6) (1.6)Чтобы выделить действие демпфирующей силы, постоянную 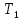 представляюткак представляюткак 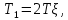 где где 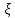 – коэффициент демпфирования. – коэффициент демпфирования. Тогда уравнение (1.6) приводится к виду: 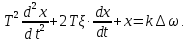 Это дифференциальное уравнение второго порядка, линейное неоднородное, с постоянными коэффициентами, поэтому на основании этого можно считать регулятор Уатта линейной непрерывной детерминированной статической системой. Используя преобразование Лапласа, а именно: 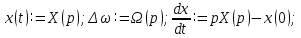 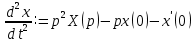 и нулевые начальные условия, можно получить операторное уравнение (1.7): 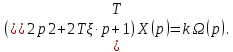 (1.7) (1.7)После введения обозначений в (1.7): 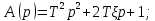 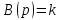 , ,операторное уравнение преобразуется к виду: 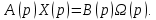 Выражение 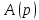 при изображении вектора состояния называется собственным оператором системы при изображении вектора состояния называется собственным оператором системы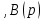 при изображении вектора воздействия – оператором воздействия при изображении вектора воздействия – оператором воздействия который может иметь смысл оператора управления или оператора возмущения. который может иметь смысл оператора управления или оператора возмущения.Из операторного уравнения можно получить передаточную функцию 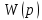 , которая определяется как отношение изображения выходного сигнала к изображению входного сигнала при нулевых начальных условиях или оператора воздействия к собственному оператору системы: , которая определяется как отношение изображения выходного сигнала к изображению входного сигнала при нулевых начальных условиях или оператора воздействия к собственному оператору системы: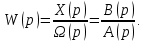 (1.8) (1.8)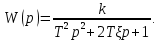 Математическая модель линейной системы может быть представлена в форме частотных характеристик. Амплитудно-фазо-частотная характеристика (АФЧХ) 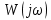 – зависимость амплитуды и фазы выходного сигнала от изменения частоты входного сигнала при его неизменных амплитуде и фазе. – зависимость амплитуды и фазы выходного сигнала от изменения частоты входного сигнала при его неизменных амплитуде и фазе.Алгоритм построения АФЧХ: в передаточной функции заменить оператор Лапласа на 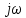 ( (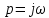 ); );выражение представить в первой алгебраической форме комплексного числа: 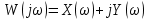 ; (1.9) ; (1.9)на комплексной плоскости построить график путем изменения частоты от нуля до бесконечности, его называют годографом. Для модели регулятора Уатта расчет АФЧХ приведен ниже. 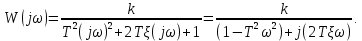 После умножения числителя и знаменателя на сопряженное выражение имеет вид: 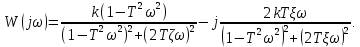 Для построения годографа (рисунок 1.6) может быть составлена таблица значений (таблица 1.1). Таблица 1.1 Значения для построения годографа
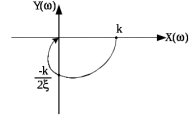 Рисунок 1.6 - АФЧХ для регулятора Уатта Амплитудно-частотная характеристика (АЧХ)– зависимость амплитуды выходного сигнала от изменения частоты входного сигнала. Эта характеристика рассчитывается как модуль АФЧХ: 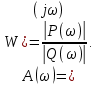 (1.10) (1.10)Для рассматриваемого примера АЧХ имеет вид: 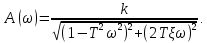 Расчет основных значений приведен в таблице 1.2, график - на рисунке 1.7. Таблица 1.2 Значения для построения АЧХ
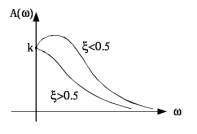 Рисунок 1.7 - График АЧХ для регулятора Уатта Фазо-частотная характеристика – изменение фазы выходного сигнала в зависимости от изменения частоты входного сигнала рассчитывается по формуле: 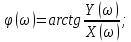 (1.11) (1.11)Тогда для регулятора Уатта она имеет вид: 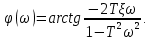 Для построения ФЧХ (рисунок 1.8) составляется таблица значений (таблица 1.3). Таблица 1.3 Значения для построения ФЧХ
 Рисунок 1.8 – ФЧХ регулятора Уатта Для того, чтобы расширить диапазон изменения частоты на графике, используется логарифмическая шкала изменения частоты. Интервал изменения частоты в десять раз называется декадой, а амплитуда измеряется в децибелах. Логарифмическая частотная характеристика (ЛАЧХ) рассчитывается по формуле: 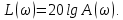 (1.12) (1.12)В ней можно выделить две асимптоты: 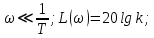 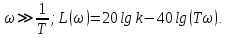 График приведен на рисунке 1.9. 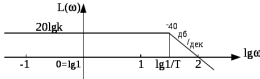 Рисунок 1.9 - Логарифмическая амплитудно-частотная характеристика Логарифмическая фазочастотная характеристика отличается от фазочастотной характеристики только масштабом по оси абсцисс и приведена на рисунке 1.10. 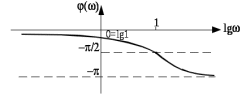 Рисунок 1.10 - Логарифмическая фазочастотная характеристика Временные характеристики изображают особенности поведения линейных систем в динамических режимах. Наиболее часто используется переходная характеристика. Она имеет вид решения дифференциального уравнения прих (0)=1, 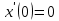 , график которой приведен на рисунке 1.11. , график которой приведен на рисунке 1.11.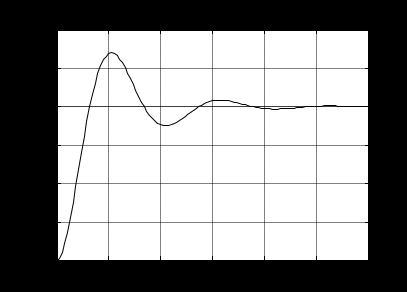 Рисунок 1.11 – Переходная характеристика для регулятора Уатта Пример 1.2. Составить уравнение и передаточную функцию электромагнитного усилителя с поперечным полем (рисунок 1.12), считая, что поток реакции полностью скомпенсирован и усилитель работает на чисто активное сопротивление. 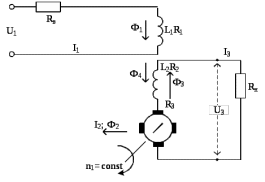 Рисунок 1.12 – Функциональная схема электромагнитного усилителя Решение: Второй закон Кирхгофа для цепи управления: 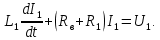 В операторной форме: 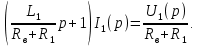 Второй закон Кирхгофа для поперечной цепи: 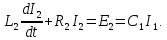 В операторной форме: 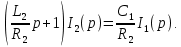 ЭДС продольной цепи пропорциональна току поперечной цепи: 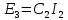 Напряжение на нагрузочном сопротивлении: 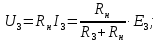 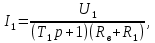 где 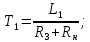 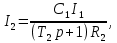 где 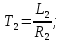 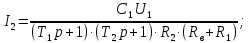 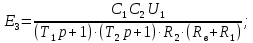 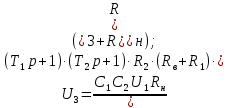 Коэффициент передачи по напряжению: 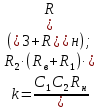 Так как 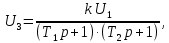 то передаточная функция имеет вид: 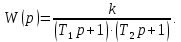 1.3 Вопросы для самопроверки Основная структурная схема САУ, ее составляющие. Система, ее основные свойства. Приведите примеры системы, докажите, что они являются системами, т.к. им свойственны все признаки. Перечислите принципы управления, на основании какого вектора проводится их классификация. Что такое закон управления? Какие приемы используются при построении линейной математической модели системы? С учетом каких требования проводится декомпозиция? Что такое передаточная функция? Как получить операторное уравнение, если известно дифференциальное уравнение? Алгоритм построения АФЧХ. Что такое АФЧ, как ее построить для линейной системы? Что показывает ФХЧ, как ее построить? Как можно расширить диапазон изменения частоты при исследовании частотных свойств системы? Как изменится АФЧХ регулятора Уатта, если коэффициент передачи увеличится? На графиках каких характеристикможно определить для передаточной функции регулятора Уатта параметры К и 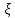 ; К иТ? ; К иТ?2 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ НА ТЕМУ «ЭЛЕМЕНТАРНЫЕ ЗВЕНЬЯ» Практическая работа посвящена исследованию характеристик элементарных звеньев путем построения пяти видов математических моделей, а именно дифференциальных и операторных уравнений, передаточных функций, частотных и переходных характеристик. Цель практического занятия: построение математической модели элементарных звеньев с использованием дифференциальных уравнений, операторных уравнений, передаточных функций, частотных характеристик, переходных характеристик. 2.1 Основные сведения из теории элементарных звеньев Элементарное звено – часть системы, имеющая математическим описанием линейное дифференциальное уравнение не выше второго порядка. При изучение элементарных звеньев используются такие формы математического описания как: дифференциальные уравнения; операторные уравнения; передаточные функции; частотные характеристики; временные характеристики. Дифференциальные уравнения получают на основании физических процессов, происходящих в реальной системе, с использованием таких приемов как декомпозиция, линеаризация и упрощение. Применение к дифференциальным уравнениям преобразования Лапласа приводят их в операторную форму. Отношение изображения выходной величины к изображению входной определяет передаточную функцию. Частотные характеристики включают амплитудно-фазовую частотную характеристику (АФЧХ), амплитудно-частотную характеристику (АЧХ), фазо-частотную характеристику (ФЧХ), логарифмическую амплитудно-частотную характеристику (ЛАЧХ) и логарифмическую фазо-частотную характеристику (ЛФЧХ). АФЧХ – зависимость амплитуды и фазы выходного сигнала от изменения частоты входного сигнала при его неизменной амплитуде и фазе. АФЧХ можно получить из передаточной функции, выполнив следующие преобразования: записать аналитическое выражение для передаточнойфункции; записать аналитическое выражение для амплитудно-фазовой частотной характеристикиW(jω), заменив p=jω,провести преобразования, учитывая, что 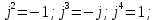 привести W(jω)к первой алгебраической форме: 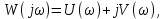 (2.1) (2.1)изменяя частоту от нуля до бесконечности, построить график W(jω), называемый годографом. АЧХ – это зависимость амплитуды выходного сигнала от изменения частоты входного сигнала при его неизменной амплитуде и фазе. АЧХ рассчитывается по формуле: 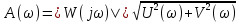 , (2.2) , (2.2)а также с использованием свойств модуля, таких как: 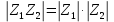 , (2.3) , (2.3)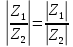 . (2.4) . (2.4)ФЧХ показывает зависимость фазы выходного сигнала от изменения частоты входного сигнала и рассчитывается по формуле (2.5): 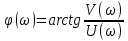 . (2.5) . (2.5)ЛАЧХ рассчитывается по формуле (2.6): L(ω) = 20lgA(ω), (2.6) графики строятся с использованием асимптотических формул. ЛФЧХ отличается от ФЧХ только масштабом по оси абсцисс, где вместо переменной ω используется lgω. К основным временным характеристикам относятся переходная характеристика (h(t)) и импульсная переходная характеристика (w(t)). Переходная характеристика – реакция системы на единичное входное воздействие при нулевых начальных условиях, а импульсная переходная характеристика – реакция на единичный импульс. Чтобы получить h(t), нужно решить дифференциальное уравнение при условии, что U(0) = 1. 2.2 Пример построения математической модели апериодического звена По схеме, приведенной на рисунке 2.1, построить все формы математического описания данной системы. 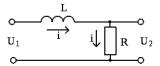 Рисунок 2.1 - Электрическая схема Дифференциальное уравнение строится на основании законов электротехники. 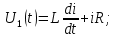 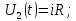 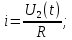 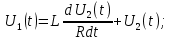 или 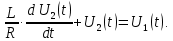 Операторное уравнение получается из дифференциального уравнения применением преобразования Лапласа: Так как 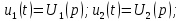 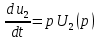 при U2(0) = 0, при U2(0) = 0,то 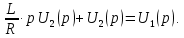 При 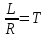 : :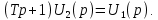 Передаточная функция. Так как передаточная функция - это отношение изображения выходного сигнала к изображению входного при нулевых начальных условиях, поэтому: 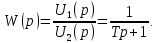 Это передаточная функция апериодического звена, у которого k = 1. Построение АФЧХ согласно алгоритма (p=jω). 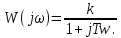 Для получения первой алгебраической формы W(jω) = Х(ω) + jУ(ω)числитель и знаменатель умножаются на сопряженное выражение: 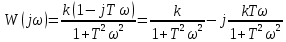 . .В таблице 2.1 приведены основные значения действительной и мнимой части. Таблица 2.1 Основные значения действительной и мнимой частей АФЧХ
Вид годографа можно определить, исключив переменную ω, т.е. получив зависимость У(Х). Так как 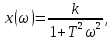 то то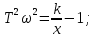 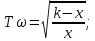 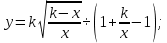 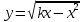 ; ;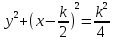 - это уравнение окружности с центром O (k/2; 0); и радиусомR = k/2. - это уравнение окружности с центром O (k/2; 0); и радиусомR = k/2.Годограф для апериодического звена приведен на рисунке 2.2. 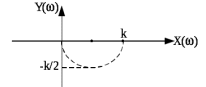 Рисунок 2.2 - Годограф апериодического звена Построение АЧХ 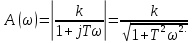 При ω = 0 A(0) = k; при ω→∞ А(ω)→0. График АЧХ при 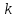 = 25 приведен на рисунке 2.3. = 25 приведен на рисунке 2.3.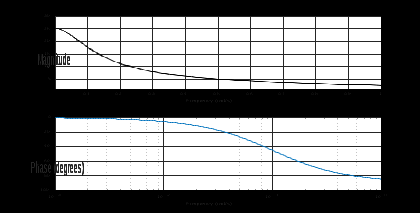 Рисунок 2.3 - График АЧХ апериодического звена Построение ФЧХ 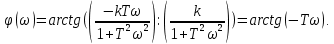 При 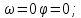 при при 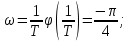 при ω→∞ при ω→∞ 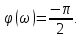 График ФЧХ апериодического звена приведен на рисунке 2.4. 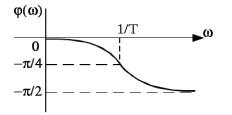 Рисунок 2.4 - График ФЧХ апериодического звена Построение ЛАЧХ 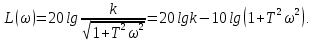 При ω<< 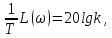 при ω>> при ω>>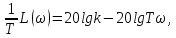 т.е. ЛАЧХ имеет две асимптоты: одну -горизонтальную, вторую, начинающуюся с частоты т.е. ЛАЧХ имеет две асимптоты: одну -горизонтальную, вторую, начинающуюся с частоты 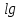 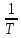 , - с наклоном 20дб/дек. Эта частота называется сопрягающей. , - с наклоном 20дб/дек. Эта частота называется сопрягающей.График ЛАЧХ апериодического звена приведен на рисунке 2.5. 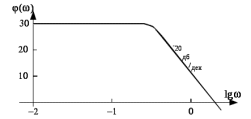 Рисунок 2.5 - График ЛАЧХ апериодического звена Построение ЛФЧХ ЛФЧХ апериодического звена отличается от ФЧХ только масштабом по оси х. График ЛФЧХ апериодического звена приведен на рисунке 2.6. 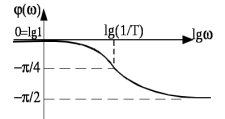 Рисунок 2.6 - График ЛФЧХ апериодического звена Построение переходной характеристики Для построения переходной характеристики апериодического звена необходимо решить дифференциальное уравнение (2.7). 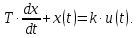 (2.7) (2.7)Частное решение линейного уравнения первого порядка при управляющем воздействии U(t) = 1(t) и начальном условии x(0) = 0 имеет вид: 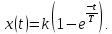 График h(t) приведен на рисунке2.7. 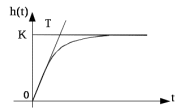 Рисунок 2.7 - График переходной характеристики апериодического звена Производная 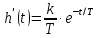 приt=0равна приt=0равна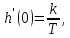 поэтому если построить касательную в начале координат, то на линии h(t)=k (линия установившегося значения) она отсекает отрезок, равный Т. поэтому если построить касательную в начале координат, то на линии h(t)=k (линия установившегося значения) она отсекает отрезок, равный Т.2.3 Задания для самостоятельной работы Для элементарных звеньев, представленных на рисунках 2.8-2.11, записать все формы математических моделей. 2.3.1 Пропорциональное звено  Рисунок 2.8 - Пропорциональное звено 2.3.2 Интегрирующее (интегральное) звено 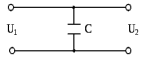 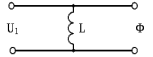 Рисунок 2.9 - Функциональная схема интегрального звена 2.3.3 Дифференцирующее звено 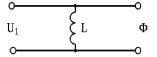 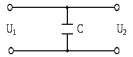 Рисунок 2.10 - Функциональная схема дифференцирующего звена 2.3.4 Колебательное звено 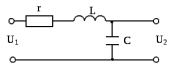 Рисунок 2.11 - Функциональная схема колебательного звена 2.4 Вопросы для самопроверки Что такое линейные непрерывные детерминированные статические системы управления? Определение элементарного звена. Формы математического описания линейных систем. Определение передаточной функции. Определение и алгоритм получения АФЧХ. Определение и алгоритм получения АЧХ. Определение и алгоритм получения ФЧХ. Определение и алгоритм получения ЛАЧХ. Чем отличается ФЧХ от ЛФЧХ? Определение переходной характеристики. Как определить установившееся значение выходной величины? Записать передаточные функции основных элементарных звеньев. Как рассчитать сопрягающую частоту? Записать (нарисовать) все формы математического описания элементарных звеньев. 3 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ НА ТЕМУ «ПОСТРОЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ СЛОЖНЫХ СИСТЕМ» Цель практического занятия: Изучение приемов построение эквивалентной передаточной функции сложных систем. 3.1 Основные сведения Передаточная функция - отношение изображения выходного сигнала к изображению входного сигнала при нулевых начальных условиях или оператора воздействия к собственному оператору системы. В линейных системах справедлив принцип суперпозиции, т.е. реакция системы на сумму воздействий равна сумме реакций на каждое воздействие в отдельности. Элементарные звенья в системах могут соединяться тремя простейшими способами: последовательно, параллельно-согласно, с обратной связью, при этом возможна замена этих соединений эквивалентными звеньями с более сложными передаточными функциями. 3.2Правила построения передаточных функций сложных систем 3.2.1 Передаточные функции последовательно соединенных звеньев перемножаются, т.е. возможно преобразование (рисунок 3.1). 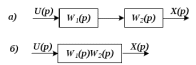 |