Учебное пособие по дисциплине Теория автоматического управления для студентов направлений
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
8.3 Задания для самостоятельной работы Используя критерий Найквиста, определить устойчивость замкнутой системы, если известна передаточная функция разомкнутой системы. Для устойчивой замкнутой системы определить запас устойчивости. 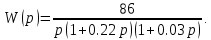 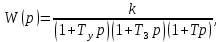 если Ty = 0,07c, T3 = 0,035c, T = 0,18c, k = 10. 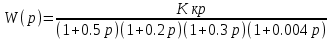 . Найти Ккр. . Найти Ккр.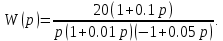 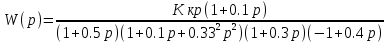 . Найти Ккр. . Найти Ккр.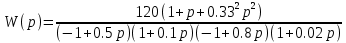 . .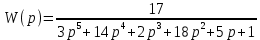 . .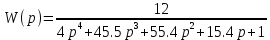 . .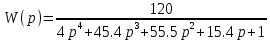 . .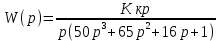 . Найти Ккр. . Найти Ккр.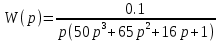 . .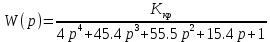 . Найти Ккр. . Найти Ккр.8.4 Вопросы для самопроверки Определение устойчивой, неустойчивой, безразлично устойчивой системы. Формулировки критерия Найквиста. Алгоритм применения критерия Найквиста. Особенности применения критерия Найквиста при наличии интегральных звеньев. Влияние коэффициента передачи на вид АФЧХ. Как определить критическое значение коэффициента передачи, используя критерий Найквиста? Как определить запас устойчивости системы по амплитуде и по фазе? Как определить устойчивость разомкнутой системы? Достаточно ли построить АФЧХ разомкнутой системы, чтобы сделать вывод об устойчивости замкнутой? Система безразлично устойчива, имеется АФЧХ разомкнутой системы, при какой дополнительной информации можно сделать вывод об устойчивости замкнутой системы? Система безразлично устойчива, имеется АФЧХ разомкнутой системы, можно ли однозначно сказать, что замкнутая система устойчива? Какой поворот на комплексной плоскости считается положительным, какой отрицательным? 9 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ НА ТЕМУ «КРИТЕРИЙ НАЙКВИСТА В ЛОГАРИФМИЧЕСКОЙ ФОРМЕ» Цель практического занятия: изучение критерия Найквиста в логарифмической форме частотных характеристик. 9.1 Теоретические сведения Частотный критерий устойчивости Найквиста позволяет определить устойчивость замкнутой системы, исследуя свойства разомкнутой системы. В зависимости от того, является ли разомкнутая система устойчивой, по виду её амплитудно-частотной характеристики делается вывод о характере устойчивости замкнутой системы. Критерий может использовать логарифмические частотные характеристики. Формулировка критерия Найквиста для логарифмических частотных характеристик: Система в замкнутом состоянии будет устойчива, если ЛАЧХ разомкнутой системы пересекает ось абсцисс при значениях фазовой характеристики, больших -. Если для положительных значений ЛАЧХ разность между числом положительных и отрицательных переходов линии -, выполненных ЛФЧХ в положительном и отрицательном направлении, равна l/2, где l- число правых корней характеристического уравнения разомкнутой системы, то система в замкнутом состоянии будет устойчива. Замечание. Переход линии (-; -2k) считается положительным, если он выполняется снизу-вверх, и отрицательным, если сверху вниз ( в АФЧХ наоборот!). 9.2 Алгоритм построения ЛАЧХ асимптотического типа При построении асимптотической ЛАЧХ придерживаются следующей последовательности. Определяется наклон первоначальной асимптоты, он равен -20νдб/дек, где ν -число интегрирующих звеньев, +20µ дб/дек, где µ-число дифференцирующих звеньев, и 0 дб/дек, если нет ни интегрирующих, ни дифференцирующих звеньев. Первоначальная асимптота проводится через точку с координатами (lg1, 20lgk). Рассчитываются сопрягающие частоты, для этого в каждом звене определяется его постоянная времени Тi, рассчитывается ωi=1/Тi, логарифм частоты lg ωi и определяется изменение наклона, присущее данному звену (апериодическое звено -20дб/дек; колебательное -40 дб/дек; форсирующее первого порядка +20 дб/дек; форсирующее второго порядка +40 дб/дек). Затем последовательно в порядке увеличения частоты, начиная от первоначальной асимптоты, строится ЛАЧХ заданной системы. ЛФЧХ может быть построена простым сложением ЛФЧХ элементарных звеньев, входящих в систему. Пример 9.1. Определить устойчивость замкнутой системы, если задана передаточная функция W(p) разомкнутой системы: 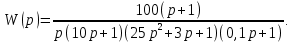 Решение: В системе имеется интегральное звено, поэтому наклон первоначальной асимптоты -20дб/дек (рисунок 9.1). Она проводится через точку (lg1; 20lg100), т.е. (lg1; 40). Т1=1; ω1=1; lg 1=0; форсирующее звено I-порядка; +20 дб/дек (3); Т2=10; ω2=0,1; lg 0,1=-1; апериодическое звено; -20 дб/дек (1); Т3=5; ω3=0,2; lg 0,2=-0,7; колебательное звено; -40 дб/дек (2); Т4=0,1; ω4=10; lg 10=1; апериодическое звено; -20 дб/дек (4).    Рисунок 9.1– Логарифмические частотные характеристики разомкнутой системы Так как ЛФЧХ пересекает линию –πпри положительном значении ЛАЧХ, замкнутая система неустойчива. 9.3 Задания для самостоятельной работы Построить ЛАЧХ и ЛФЧХ системы, определить устойчивость; если она устойчива, то определить запас устойчивости по амплитуде и фазе. 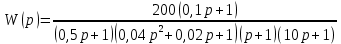 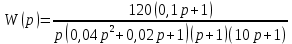 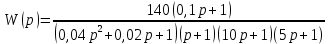 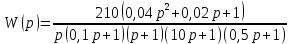 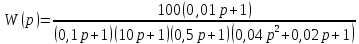 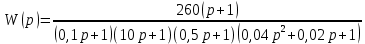 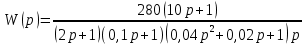 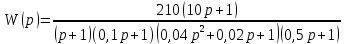 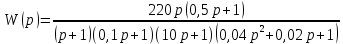 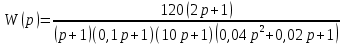 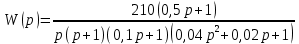 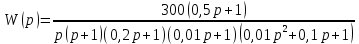 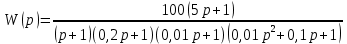 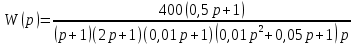 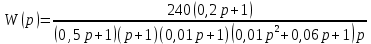 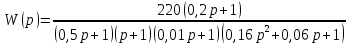 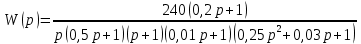 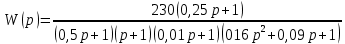 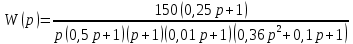 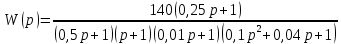 9.4Вопросы для самопроверки Определение логарифмических частотных характеристик. Что такое декада, децибел? Алгоритм построения ЛАЧХ и ЛФЧХ. Формулировка критерия Найквиста в логарифмической форме. Какой переход считается положительным, какой отрицательным? Что такое сопрягающая частота? Как меняется наклон асимптоты в сопрягающей частоте для элементарных звеньев? Как определить наклон первоначальной асимптоты? Запас устойчивости по амплитуде и по фазе. Изменится ли запас устойчивости при изменении коэффициента передачи, если изменится, то как? Как определить устойчивость разомкнутой системы? Как по теореме Ляпунова определить, что система безразлично устойчивая? Как определить, что в разомкнутой системе есть интегральные звенья? Какой поворот на комплексной плоскости считается положительным, какой отрицательным? 10 ПРАКТИЧЕСКОЕ ЗАНЯТИЯ НА ТЕМУ «D-РАЗБИЕНИЕ ПО ОДНОМУ ПАРАМЕТРУ» Цель практического занятия: ознакомление с методами расчета пределов изменения параметра, обеспечивающих устойчивость системы. Основные сведения Критерии устойчивости позволяют не только сделать заключение о характере устойчивости при заданных параметрах системы, но и выяснить степень влияния их на устойчивость, определить предельные (критические) значения параметров (коэффициентов передачи, постоянных времени), при которых система становится неустойчивой. Для этого разработаны специальные методы исследования, к которым относятся метод корневого годографа, метод Д-разбиения. Эти методы используют особенности перемещения корней характеристического уравнения на комплексной плоскости при изменении коэффициентов характеристического уравнения. Пусть характеристическое уравнение системы имеет вид: 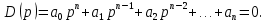 (10.1) (10.1)При заданных коэффициентах уравнение имеет вполне определенные корни, например, m – в правой полуплоскости, (n – m) – в левой. Изменение коэффициентов приводит к перемещению корней на комплексной полуплоскости. Это перемещение называется корневым годографом. При некотором сочетании коэффициентов корень может попасть в начало координат или на мнимую ось, тогда значения корней соответствуют характеристическому уравнению при a0=1: 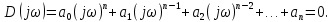 (10.2) (10.2)Это уравнение в n-мерном пространстве коэффициентов с осями (a1;a2;…an). Тогда при заданном значении частоты ему соответствует некоторая точка, при изменении частоты образуется гиперповерхность. При изменении значений коэффициентов при их некотором сочетании уравнение гиперповерхности может обращаться в ноль D(j) = 0, при этом произойдет переход одного действительного или двух комплексных корней из одной полуплоскости в другую (из левой в правую, из правой в левую). Для исследования влияния одного параметра на устойчивость системы используется следующий алгоритм. Характеристический полином необходимо представить в виде: 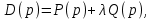 (10.3) (10.3)где λ - исследуемый параметр. Затем нужно заменить оператор р на j и вывести характеристическое уравнение на границу D-разбиения: 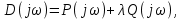 (10.4) (10.4)Из этого уравнения необходимо выразить исследуемый параметрλ и представить его в первой алгебраической форме комплексного числа: 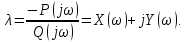 (10.5) (10.5)Изменяя частоту от нуля до бесконечности, построить половину границы, на ней выполнить штриховку слева от границы при движении в сторону увеличения частоты (рисунок 10.1). 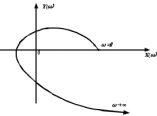 Рисунок 10.1 – Изображение половины границы устойчивости Используя свойство симметричности комплексной функции относительно действительной полуоси, вторая половина строится отражением относительно оси абсцисс, что соответствует изменению частоты от минус бесконечности до нуля (рисунок 10.2). Точки пересечения линий на годографе называются узлами. На рисунке 10.2, например, это точка А. 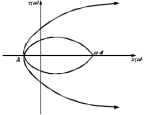 Рисунок 10.2 – Изображение границы устойчивости после отражения относительно оси абсцисс Область с внутренней штриховкой может быть областью устойчивости D0, поэтому в этой области выбирается любое значение λ(самое простое, например, равное нулю), подставляется в характеристическое уравнение и проверяется устойчивость по любому критерию, например, по теореме Ляпунова. Если в этой точке система оказалась устойчивой, то она будет устойчива в любой точке этой области (рисунок 10.3).  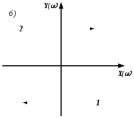 Рисунок 10.3 – Пример области D-разбиения: а) – область с внутренней штриховкой; б) – переход комплексных корней из левой полуплоскости в правую (1); из правой в левую (2) Если система устойчива в области D0, то определяется ее состояние в других областях. Если пересечение границы происходит по направлению штриховки (направление 1), то один корень в плоскости D-разбиения переходит из правой полуплоскости в левую; если переход оказывается против штриховки, то добавляется правый корень (направление 2). Таким образом, на рисунке 3 в области D1 один правый корень (если D0– область устойчивости), в области D2 два правых корня. Точки пересечения с вещественной полуосью определяют критические значения параметра. Интервал изменения исследуемого параметра выбирается среди действительных положительных значений. Если в области D0система оказалась неустойчивой, то изменением этого параметра добиться устойчивости системы нельзя, нужно применять другие приемы, например, введение корректирующего устройства. Пример10.1. Используя метод D-разбиения, определить границы изменения коэффициента передачи, обеспечивающего устойчивость замкнутой системы с характеристическим уравнением: 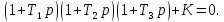 Решение: Выделяется исследуемый параметр( 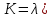 : :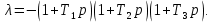 После подстановки р =j, выделения действительной и мнимой частей комплексный параметр равен: λ() 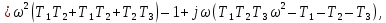 т.е. 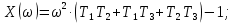 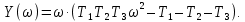 Точки пересечения с осью абсцисс находятся из равенства: 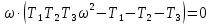 , ,полученные значения частоты подставляются в Х(), точки пересечения с осью ординат - из равенства: 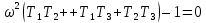 , , тогда значения частоты нужно подставить в Y(). Для 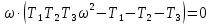 корни равны: корни равны: = 0, 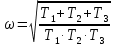 , ,Х () = - 1; 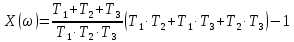 (точка Б). (точка Б).Для 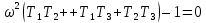 корень равен: корень равен: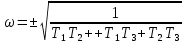 . .Годограф пересекает ось ординат в точках: 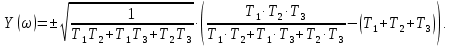 Граница D-разбиения приведена на рисунке 10.4.  Рисунок 10.4 – Граница D-разбиения к примеру 10.1 В области D0 выбирается значение λ=0, тогда характеристическое уравнение имеет вид: 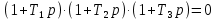 , ,это уравнение имеет три отрицательных действительных корня (-1/Т1; -1/Т2; -1/Т3), следовательно, в этой точке система устойчива, значит сохраняет устойчивость внутри всей области D0. При пересечении границы из области D0в область D1 движение происходит против штриховки, поэтому в области D1один правый корень, в области D2– два правых корня. Таким образом при изменении коэффициента передачи от нуля до значения в точке Б система будет устойчива. |
