Учебное пособие по дисциплине Теория автоматического управления для студентов направлений

• Название: Учебное пособие по дисциплине Теория автоматического управления для студентов направлений
• Дата: 18.02.2022
• Размер: 2.41 Mb.
• Имя файла: -.docx
• Тип: Учебное пособие; #366287
• страница: 6 из 9

7.2 Задания для самостоятельной работы
7.2.1 Исследовать устойчивость системы по критерию Михайлова, если задано ее характеристическое уравнение:

а)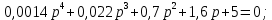

б)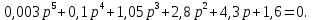

7.2.2 Используя критерий Михайлова в форме перемежающихся корней, исследовать систему на устойчивость, если она задана характеристическим уравнением:

а)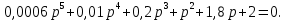

б)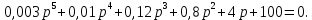

7.2.3 Рассчитать критическое значение параметра К_р для системы, заданной характеристическим уравнением: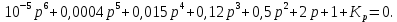


7.3Вопросы для самопроверки

1. 
   Что такое функция Михайлова?
   
2. 
   Как составить функцию Михайлова?
   
3. 
   Что должно быть известно, чтобы построить функцию Михайлова?
   
4. 
   Что такое годограф Михайлова?
   
5. 
   Как по известному годографу определить устойчивость системы?
   
6. 
   Как схематично можно построить годограф Михайлова?
   
7. 
   Как можно определить устойчивость системы по таблице изменения действительной и мнимой частей функции Михайлова в зависимости от изменения частоты?
   
8. 
   Каким образом нужно представить информацию о влиянии изменения частоты в декартовой системе координат, чтобы исследовать устойчивость системы по критерию Михайлова?
   
9. 
   Алгоритм расчета критического значения параметра по критерию Михайлова.
   

8 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ НА ТЕМУ «КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА»

Цель практического занятия: изучение особенностей применения критерия Найквиста

8.1 Формулировки и алгоритм применения критерия Найквиста

8.1.1 Первая формулировка критерия Найквиста, наиболее часто встречающаяся: Если разомкнутая система автоматического управления (САУ) устойчива, то замкнутая система будет устойчива, если амплитудно-фазовая частотная характеристика (АФЧХ) разомкнутой системы не охватывает точку (-1;j0).

Алгоритм применения:

• 
  убедиться в устойчивости разомкнутой системы (по теореме Ляпунова, критерию Гурвица или Михайлова);
  
• 
  построить АФЧХ разомкнутой системы;
  
• 
  сделать вывод об устойчивости замкнутой системы.
  

8.1.2 Вторая формулировка критерия Найквиста: Если разомкнутая система автоматического управления неустойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика системы при изменении частотыωот 0 до∞охватывала точку (-1; j0) в положительном направленииl/2 раз, гдеl– число правых корней характеристического уравнения разомкнутой системы.

8.1.3 Третья формулировка критерия Найквиста:Если разомкнутая САУ неустойчива, то для того, чтобы замкнутая САУ была устойчива, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов АФЧХ в интервале действительной полуоси (-∞; -1) была равна l/2, гдеl– число правых корней характеристического уравнения разомкнутой системы.

Замечание. Переход считается положительным, если выполняется сверху вниз и отрицательным, если снизу-вверх (рисунок 8.1).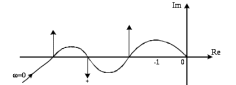



Рисунок 8.1- Иллюстрация типа перехода АФЧХ действительной полуоси

8.1.4 Учет астатизма

Если в разомкнутой системе имеются интегрирующие звенья, то прежде чем применить ту или иную формулировку, АФЧХ дополняется дугой бесконечно большого радиуса на угол π/2∙ν против часовой стрелки, где ν число интегрирующих звеньев.

На рисунке 8.2 приведена АФЧХ разомкнутой устойчивой системы с астатизмом второго порядка (=2).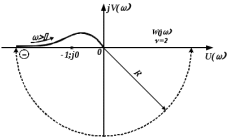



Рисунок 8.2 -АФЧХ разомкнутой системы (ν=2)

Так как АФЧХ после дополнения дугой бесконечно большого радиуса на угол π/2∙2= π охватывает точку (-1; j0), то система в замкнутом состоянии будет неустойчива.

На рисунке 8.3 приведена АФЧХ разомкнутой устойчивой системы, имеющей два интегрирующих звена (ν=2).

После дополнения дугой бесконечно большого радиуса на угол π/2∙ν АФЧХ разомкнутой системы не охватывает точку (-1; j0). Система в замкнутом состоянии будет устойчива.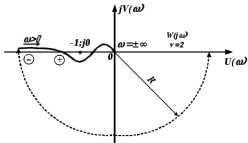



Рисунок 8.3-АФЧХ разомкнутой системы с астатизмом второго порядка

8.1.5 Запас устойчивости по амплитуде и по фазе

Используя критерий Найквиста, можно определить запас устойчивости по фазе и амплитуде, что является весьма существенным моментом, т.к. параметры системы могут несколько изменяться в процессе работы.

Запас устойчивости по амплитудеhопределяется как расстояние между точкой (-1;j0) и точкой пересечения графика W(jω)вещественной оси правее точки (-1;j0)(рисунок 8.4), запас устойчивости по фазе φ- угол между отрицательной полуосью и линией, соединяющей начало координат и точку пересечения АФЧХ и окружности с радиусом, равным единице.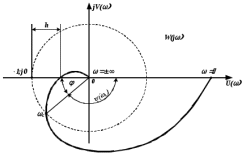



Рисунок 8.4 -Определение запаса по амплитуде и по фазе для систем с внутренними обратными связями

Замечание. При решении обратной задачи, т.е. задачи обеспечения нужного запаса устойчивости, строят запретные зоны.

8.2 Примеры определения устойчивости системы по критерию Найквиста

Пример 8.1. Исследовать устойчивость замкнутой системы, приведенной на рисунке 5.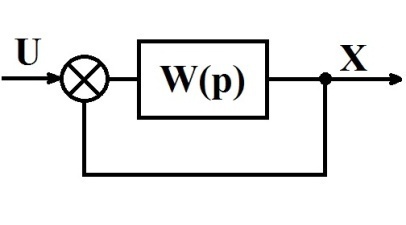



Рисунок 8.5— Структурная схема к примеру 8.1

Передаточная функция разомкнутой системы имеет вид: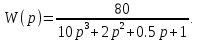



Решение: Характеристическое уравнение разомкнутой системы определяется знаменателем передаточной функции: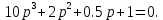



Корни характеристического уравнения рассчитываются в пакете Matlab:

p=[10 2 0.5 1]

roots (p)

и равны: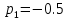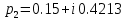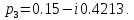







Так как два корня имеют положительные действительные части, то разомкнутая система неустойчивая.

АФЧХ разомкнутой системы, построенная в пакете Matlab, приведена на рисунке 8.6. Для этого были использованы команды:

sys1=tf([80], [10 2 0.5 1])

nyquist(sys1)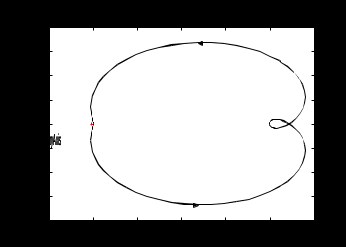



Рисунок 8.6 — АФЧХ разомкнутой системы для примера 8.1

Т.к. разомкнутая система неустойчивая, АФЧХ разомкнутой системы не охватывает точку (-1; j0), то по второй формулировке критерия Найквиста замкнутая система неустойчива.

Чтобы определить значение коэффициента передачи, при котором замкнутая система будет находиться на границе устойчивости, надо записать выражение для АФЧХ разомкнутой системы и приравнять его -1: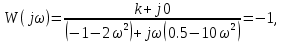



тогда: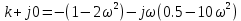

.

По свойству комплексных чисел: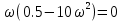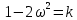

,

.

Таким образом, из первого уравнения: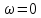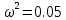

,

,

из второго: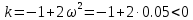

.

Коэффициент передачи — параметр в системах положительный, т.е. изменением коэффициента передачи этой системы данная замкнутая система не станет устойчивой.

Пример 8.2. Определить устойчивость замкнутой системы (рисунок 8.5), если разомкнутая система задана передаточной функцией: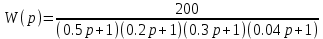

.

Решение: Характеристическое уравнение: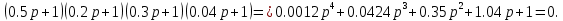



имеет корни: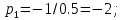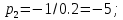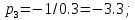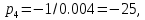









а так как действительные части отрицательные, то разомкнутая система устойчива.

А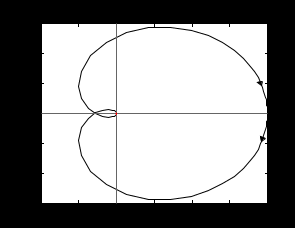
ФЧХ разомкнутой системы (рисунок 8.7) охватывает точку (-1; j0), по первой формулировке замкнутая система неустойчива.

Рисунок 8.7 — АФЧХ разомкнутой системы к примеру 8.2

Пример 8.3.Определить, устойчива ли замкнутая система, если устойчива, то определить запас устойчивости. Разомкнутая система задана передаточной функцией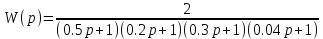

.

Решение: Согласно примера 8.2, разомкнутая система устойчива.



Рисунок 8.9 — АФЧХ разомкнутой системы для примера 8.3

Замкнутая система устойчива, т.к. АФЧХ разомкнутой системы не охватывает точку (-1;j0).

Чтобы рассчитать запас устойчивости по амплитуде, надо найти точку пересечения оси Ох амплитудно-фазочастотной характеристикой, в этой точке ордината равна нулю.

АФЧХ в первой алгебраической форме: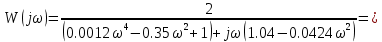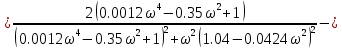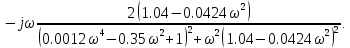







В точке пересечения оси абсцисс мнимая часть равна нулю, т.е. ее числитель равен нулю: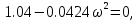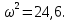





При этой частоте действительная часть (второе слагаемое в знаменателе равно нулю):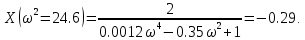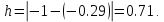





Чтобы сосчитать запас устойчивости по фазе, надо модуль АФЧХ приравнять единице, найти значение частоты, при этом значении вычислить Y(ω) иX(ω) найти угол .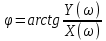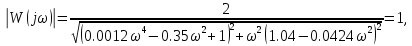



т.е. .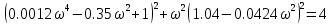

После раскрытия скобок и приведения подобных было получено: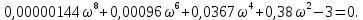



Корни :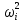

-626,68

-22,53±12,14i

+5,07.
Таким образом,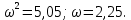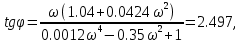



что соответствует углу .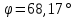

Запас устойчивости по амплитуде (расстояние до точки (-1; j0)) составил h=0.71, по фазе φ= 68,17^о. Из рассмотренных примеров можно сделать вывод, что выбор коэффициента передачи влияет на вид АФЧХ: чем больше k, тем шире АФЧХ. Устойчивость замкнутой системы может зависеть от коэффициента передачи прямой цепи k.

Если выбор коэффициента передачи влияет на устойчивость замкнутой системы, то можно вычислить критическое значение коэффициента передачи. Это происходит, когда АФЧХ разомкнутой системы проходит через точку (-1; j0), замкнутая система находится на границе устойчивости.

Пример 8.4.Для замкнутой системы определить значение коэффициента передачи разомкнутой системы, при котором замкнутая система находится на границе устойчивости. Передаточная функция разомкнутой системы W(p):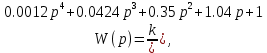



Решение: АФЧХ разомкнутой системы на границе устойчивости проходит через точку (-1; j0):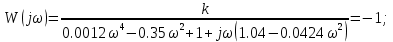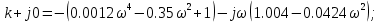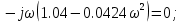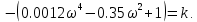









Из первого уравнения: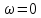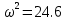

;

.

Из второго: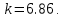



Таким образом, при 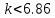-замкнутая система будет устойчива.

Пример 8.5.Исследовать влияние интегрирующих звеньев на устойчивость замкнутой системы, если разомкнутая система имеет передаточную функцию W(p):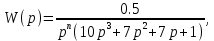



где n — число интегрирующих звеньев.

Решение:

1. 
   Если n = 0, т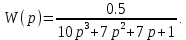о
   

Корни характеристического уравнения равны:

p_1,2=-0.2683±j0,7351;

p₃=-0.1633,

таким образом, разомкнутая система устойчива.

АФЧХ разомкнутой системы приведена на рисунке 8.10.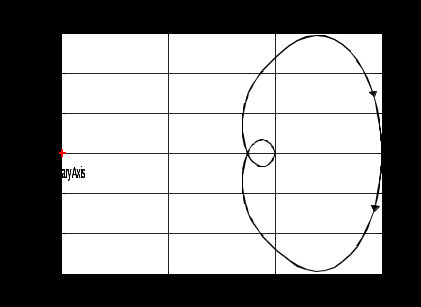



Рисунок 8.10 — АФЧХ разомкнутой системы при n = 0
Замкнутая система устойчива.

2. 
   Если n = 1, т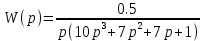о
   

Корни характеристического уравнения равны: p₁=0, p_2,3=-0.2683±j0,7351; p₄=-0.1633, таким образом, разомкнутая система безразлично устойчива, т.к. кроме корней с отрицательной действительной частью есть нулевой корень. АФЧХ этой системы приведена на рисунке 8.11.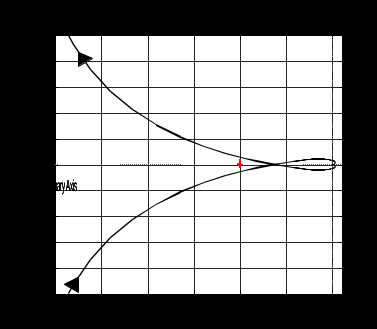



Р исунок 8.11— АФЧХ разомкнутой системы при одном интегральном звене (n = 1)

После добавления АФЧХ дугой бесконечно большого радиуса на одну четверть, она не охватывает точку (-1; j0), замкнутая система устойчива.

3. 
   При n 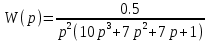= 2,
   

Разомкнутая система безразлично устойчива, АФЧХ приведена на рисунке 8.12.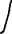



Р исунок 8.12 — АФЧХ разомкнутой системы при двух интегрирующих звеньях

З амкнутая система неустойчива, т.к. после добавления дугой бесконечно большого радиуса на две четверти АФЧХ разомкнутой системы охватывает точку (-1; j0).

При наличии трех интегральных звеньев АФЧХ, после добавления дугой на три четверти, охватывает точку(-1;j0), замкнутая система не устойчива (рисунок 8.13).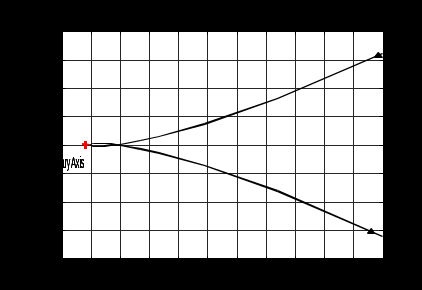



Р исунок 8.13 — АФЧХ разомкнутой системы при наличии трех интегральных звеньев

В ывод: введение интегральных звеньев в разомкнутую систему может привести замкнутую систему в неустойчивое состояние.