Учебное пособие по дисциплине Теория автоматического управления для студентов направлений
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
4.2 Преобразование последовательного соединения элементов в параллельно-согласное Последовательное соединение элементов (рисунок 4.4) может быть преобразовано в эквивалентное параллельно-согласное соединение. 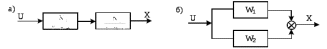 Рисунок 4.4 – Преобразование последовательного соединения элементов в параллельно-согласное: а) исходная схема; б) после преобразования Пусть передаточная функция для исходной системы имеет вид: 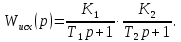 (4.4) (4.4)При параллельно-согласном соединении передаточные функции складываются, поэтому исходная передаточная функция может быть представлена как: 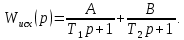 Коэффициенты передачи А и В могут быть рассчитаны методом неопределенных коэффициентов, в котором используется разложение на простые дроби. 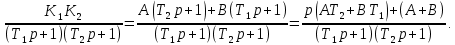 Тогда система уравнений для расчета коэффициентов имеет вид: 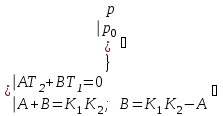 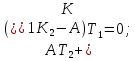 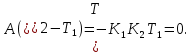 Коэффициенты А и В, рассчитанные по системе уравнений, равны: 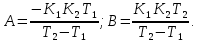 Тогда передаточные функции элементов, включенных параллельно-согласно, имеют вид: 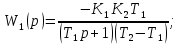 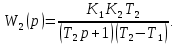 и структурная схема приведена на рисунке 4.5.  Рисунок 4.5 – Структурная схема эквивалентного параллельно-согласного соединения При таком преобразовании набор элементов не изменяется, изменяются коэффициенты передачи, причем у одного элемента он будет иметь отрицательное значение. 4.3 Преобразование параллельно-согласного соединения элементов в последовательное соединение Схему с параллельно-согласным соединением элементов можно преобразовать в схему с последовательным соединением элементов. На рисунке 4.6 приведено параллельно-согласное соединение, которое необходимо преобразовать в эквивалентное последовательное соединение.  Рисунок 4.6 – Исходная структурная схема с параллельно-согласным соединением элементов Передаточная функция исходной структурной схемы равна: 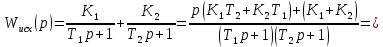 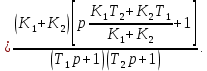 Данная передаточная функция соответствует структурной схеме, приведенной на рисунке 4.7, где элементы соединены последовательно.  Рисунок 4.7 – Эквивалентная структурная схема с последовательным соединением элементов 4.4 Преобразование структурной схемы с обратной связью в последовательное соединение элементов Исходная структурная схема приведена на рисунке 4.8.  Рисунок 4.8 – Исходная структурная схема с обратной связью Эквивалентная передаточная функция равна: 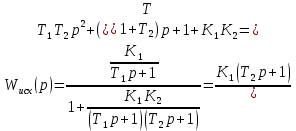 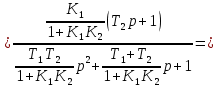 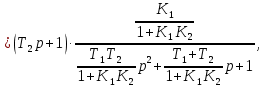 что соответствует последовательному соединению звена второго порядка (в зависимости от соотношения параметров или колебательное звено, или два апериодических звена) и форсирующего звена первого порядка. Структурная схема эквивалентного последовательного соединения приведена на рисунке 4.9.  Рисунок 4.9 –Структурная схема последовательного соединения 4.5 Задания для самостоятельной работы 4.5.1 Преобразовать последовательное соединение звеньев (рисунок 4.10) в параллельно-согласное соединение.  Рисунок 4.10 – Структурная схема к примеру 4.3.1 4.5.2 Преобразовать параллельно-согласное соединение звеньев в эквивалентное последовательное соединение (рисунок 4.11). 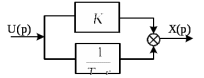 Рисунок 4.11 – Структурная схема к примеру 4.3.2 4.5.3 Преобразовать соединение звеньев с обратной связью в последовательное соединение (рисунок 4.12).  Рисунок 4.12 – Структурная схема к примеру 4.3.3 4.6 Вопросы для самопроверки Какое соединение называется последовательным? Какое соединение называется параллельно-согласным? Какое соединение называется с обратной связью? Изменяется ли набор элементарных звеньев при изменении способа соединения? Остаются ли неизменными параметры элементарных звеньев при изменении способа соединения? 6) Выведите формулу эквивалентной передаточной функции при последовательном соединении двух звеньев. 7) Выведите формулу эквивалентной передаточной функции при параллельном соединении двух звеньев. 9) Выведите формулу эквивалентной передаточной функции при соединении двух элементов с обратной связью. 5 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ НА ТЕМУ «ВЛИЯНИЕ ОБРАТНОЙ СВЯЗИ НА СВОЙСТВА СИСТЕМЫ» Цель практического занятия: Изучение различных видов обратной связи и их влияние на свойства системы. 5.1 Основные определения Соединение называется соединением с обратной связью, если часть сигнала или весь сигнал с выхода подается обратно на вход, причем если сигнал подается со знаком плюс, то обратная связь называется положительной, если со знаком минус, то отрицательной. Обратная связь называется жесткой, если она представлена пропорциональным звеном. Жесткая обратная связь с коэффициентом передачи, равным единице, называется единичной. Обратная связь, в цепи которой находится любые другие элементы, кроме пропорционального, называется гибкой. Введение обратной связи влияет на свойства системы. 5.2 Исследование влияния обратной связи на элементарные звенья Пример 5.1. Исследовать влияние жесткой обратной связи на свойства апериодического звена (рисунок 5.1).  Рисунок 5.1 – Структурная схема к примеру 5.1 Передаточная функция замкнутого контура имеет вид: 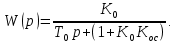 (5.1) (5.1)После приведения к канонической форме: 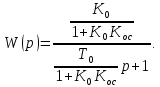 Звено осталось апериодическим, изменились его параметры. ЕслиК0=10, Т0= 1, Кос=0,09, тогда Кэкв=5,26; Тэкв= 0,526, т.е. коэффициент передачи уменьшился, постоянная времени также уменьшилась. Если Кос = 5, то Кэкв =0,19;Тэкв =0,19. При введении жесткой обратной связи уменьшается и коэффициент передачи, и постоянная времени звена. Уменьшение последней приводит к тому, что длительность переходного процесса уменьшается. Пример 5.2. Исследовать влияние положительной жесткой обратной связи на апериодическое звено. Передаточная функция замкнутого контура с положительной обратной связью (рисунок 5.2) имеет вид: 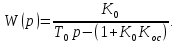 (5.2) (5.2)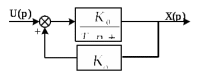 Рисунок 5.2 – Структурная схема контура с положительной обратной связью После приведения к каноническому виду: 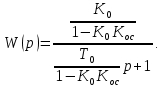 При наличии жесткой положительной обратной связи контур может стать неустойчивым, если 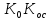 будет иметь значение больше единицы. Если значение будет иметь значение больше единицы. Если значение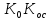 будет иметь значение меньше единицы, то останется тем же апериодическим звеном, но коэффициент передачи и постоянная времени станут больше. будет иметь значение меньше единицы, то останется тем же апериодическим звеном, но коэффициент передачи и постоянная времени станут больше.Пример 5.3. Звено апериодическое охвачено гибкой обратной связью в виде реального дифференцирующего звена (рисунок 5.3).  Рисунок 5.3 – Структурная схема к примеру 5.3 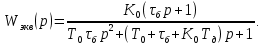 Дискриминант знаменателя имеет вид: 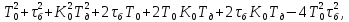 при его положительных значениях контур будет эквивалентен последовательному соединению трех звеньев: форсирующего первого порядка и двух апериодических; при отрицательных значениях дискриминанта контур эквивалентен последовательному соединению двух форсирующих звеньев первого порядка и колебательного звена. 5.3 Задания для самостоятельной работы 1) Исследовать влияние жесткой обратной связи, которая охватывает колебательное звено. 2) Исследовать влияние обратной связи в форме апериодического звена на колебательное звено в прямой цепи. 5.4Вопросы для самопроверки Приводит ли жесткая обратная связь к изменению типа звена, которое она охватывает? Приведите пример. Сохраняется ли тип звена при использовании гибкой обратной связи? Какая обратная связь называется жесткой? Чем отличается жесткая обратная связь от гибкой? К каким изменениям в схеме приводит использование жесткой отрицательной обратной связи? Какое соединение называется с обратной связью? Чем отличается отрицательная обратная связь от положительной? К какому типу относится единичная обратная связь? 6 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ НА ТЕМУ «АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ» Цель практического занятия: изучение методов определения устойчивости линейной непрерывной системы по характеристическому уравнению. 6.1 Основные определения Свойство устойчивости систем является одним из наиболее важных для её работоспособности, линейная система автоматического управления считается устойчивой, если после окончания воздействия по истечении некоторого времени она возвращается в исходное состояние (с точностью до проведенных измерений). Если после окончания воздействия система неограниченно отдаляется от исходного состоянии, то её называют неустойчивой. Если после окончания воздействия система приходит в другое состояние, отличное от исходного, то её называют безразлично устойчивой. 6.2 Необходимый признак устойчивости Линейная непрерывная детерминированная статическая система может быть устойчива, если все коэффициенты характеристического уравнения положительны. Характеристическое уравнение можно получить, приравняв к нулю, собственный оператор системы, т.е. знаменатель передаточной функции. Пример 6.1. Могут ли быть устойчивы системы характеристические уравнения которых приведены ниже: 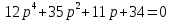 ; ;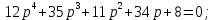 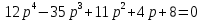 . .В характеристическом уравнении примера а) отсутствует третья степень, т.е. коэффициент равен нулю, поэтому система, представленная уравнением а), неустойчива. В характеристическом уравнении б) все коэффициенты положительны, поэтому эта система может быть устойчива (а может быть неустойчивой!). В характеристическом уравнении в) есть отрицательный коэффициент (при третьей степени), поэтому система неустойчива. 6.3 Теорема Ляпунова 6.3.1 Алгоритм применения теоремы Ляпунова Устойчивость системы можно определить, исследуя её математическое описание (дифференциальное уравнение, операторное уравнение, передаточную функцию, частотные или временные характеристики). Математическое описание поведения системы получают на основе физических закономерностей процессов, используя различные приемы, такие как декомпозиция, линеаризация и упрощение. Такие дифференциальные уравнения называют линейными дифференциальными уравнениями первого приближения. Очень часто они имеют вид линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, решение которых определяется в виде суммы двух слагаемых: свободной составляющей и вынужденной, вызванной внешними воздействиями: 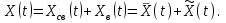 (6.1) (6.1) Свободная составляющая 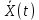 определяется только свойствами системы. Это решение линейного однородного дифференциального уравнения (ЛОДУ), которое находится на основе характеристического уравнения. определяется только свойствами системы. Это решение линейного однородного дифференциального уравнения (ЛОДУ), которое находится на основе характеристического уравнения.В соответствии с определением устойчивости по А.М. Ляпунову система будет асимптотически устойчива, если с течением времени при t 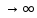 свободная составляющая будет стремиться к нулю, т.е. свободная составляющая будет стремиться к нулю, т.е. 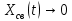 или или  . .Решение ЛОДУ определяется как линейная комбинация решений вида  ; ; ; ; ; ;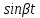 , , 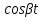 или в общем случае или в общем случае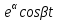 и и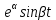 , где , где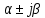 – корни характеристического уравнения, – корни характеристического уравнения,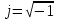 . Для того, чтобы . Для того, чтобы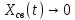 , действительная часть корней характеристического уравнения должна быть отрицательной. , действительная часть корней характеристического уравнения должна быть отрицательной.Таким образом, условие устойчивости линейной системы может быть сформулировано следующим образом: для того, чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни её характеристического уравнения имели отрицательные действительные части, т.е. были левыми. Пример 6.2.Определить устойчива ли система, еслиона имеет передаточную функцию: 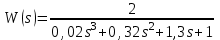 . .Решение: Характеристическое уравнение для такой системы имеет вид 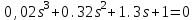 . .Корни характеристического уравнения s1= –1; s2=–10, s3=–5 имеют отрицательные действительные части, следовательно, система устойчива. 6.3.2 Вычисление корней в программе Matlab Задается полином, для которого необходимо найти корни, корни рассчитываются командой roots(P). Пример расчета корней для задания 6.2: Р=[0.02 0.32 1.3 1] Р=0.02 0.32 1.3 1 roots (P) -1 -5 -10 6.4 Критерий устойчивости Гурвица 6.4.1 Алгоритм применения критерия Гурвица Устойчивость линейной системы можно определить, не вычисляя корней характеристического уравнения, с помощью критериев устойчивости. С развитием вычислительной техники проблемы определения корней характеристического уравнения нет, однако критерии устойчивости могут ответить на другие вопросы, такие как: каков запас устойчивости, что нужно сделать, чтобы неустойчивая система стала устойчивой и т.д. Критерии устойчивости делятся на алгебраические и частотные. Алгебраические критерии исследуют коэффициенты характеристического уравнения, частотные строятся на основе либо характеристического уравнения, либо передаточной функции. Наиболее известным алгебраическим критерием является критерий Гурвица (1895г). Из коэффициентов характеристического уравнения: 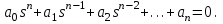 (6.2) (6.2)строится главный определитель Гурвица ∆n: 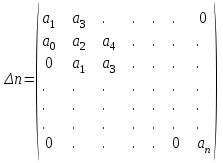 (6.3) (6.3)Если все определители, построенные от верхнего левого угла: 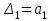 ; ;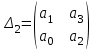 ; ;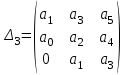 … …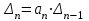 . .– положительны, то система устойчива, если среди них есть отрицательные, то неустойчива. Кроме того, критерий позволяет определить значения параметров системы, обеспечивающие ее устойчивость. Для этого ∆n–1 приравнивается нулю (система находится на границе устойчивости) и получившееся уравнение разрешается относительно интересующего параметра. Замечание. Так как 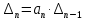 , а по необходимому условию устойчивости все коэффициенты характеристического уравнения положительны, то знак ∆n определяется знаком ∆n-1. , а по необходимому условию устойчивости все коэффициенты характеристического уравнения положительны, то знак ∆n определяется знаком ∆n-1.Пример 6.3. Используя критерий Гурвица, определить устойчивость системы, если характеристическое уравнение имеет вид: 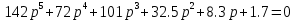 . .Решение: Главный определитель Гурвица: 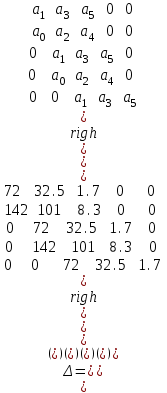 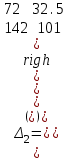 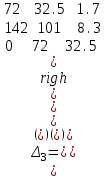 ; ;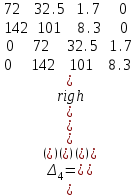 Так как все определители получились положительными, то характеристическое уравнение принадлежит устойчивой системе. 6.4.2 Вычисление определителей в программе Matlab Расчет определителей в программе Matlab выполняется с помощью последовательности команд. Задание матрицы: присваивается имя, далее в квадратных скобках построчно через точку с запятой (;) записываются все коэффициенты характеристичного уравнения: 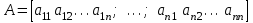 A= 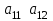 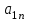 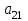 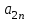 … 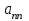 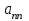 Расчет определителя: det (A) Пример расчета определителя: 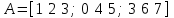 A = 1 2 3 0 4 5 3 6 7 det (A) А=-8. |
