Учебное пособие по дисциплине Теория автоматического управления для студентов направлений
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
Задания для самостоятельной работы 1) Для замкнутой систему управления с характеристическим уравнением: 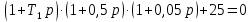 выделить область устойчивости по параметру T1. 2) Построить область устойчивости по параметру К для системы с характеристическим уравнением: 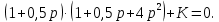 10.3 Вопросы для самопроверки Сформулируйте алгоритм Д-разбиения. В какой форме необходимо представить исследуемый параметр? Как можно определить точки пересечения с осями на комплексной плоскости? Что для системы определяет точка пересечения с осью абсцисс? Если в области с внутренней штриховкой система оказалась неустойчивой, можно ли выбрать интервал изменения исследуемого параметра, где система будет устойчива? Как изменится количество левых корней характеристического уравнения при переходе через узел годографа? Поясните, почему при переходе границы против штриховки, появляется правый корень. 11 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ НА ТЕМУ «ОПРЕДЕЛЕНИЕ ИНТЕРВАЛОВ ИЗМЕНЕНИЯ ДВУХ ПАРАМЕТРОВ МЕТОДОМ D-РАЗБИЕНИЯ» Цель практического занятия: изучение алгоритма определения интервалов изменения двух параметров, при которых система остается устойчивой, методом D-разбиения. Основные сведения Изменение параметров системы (коэффициента, передачи, постоянных времени) может влиять на устойчивость системы. Для расчета интервалов их допустимого изменения может использоваться метод D-разбиения по двум параметрам. Если параметры входят в характеристическое уравнение линейно, то применяется следующий алгоритм. В характеристическом уравнении выделяются слагаемые, в которые входят исследуемые параметры, а также свободные от них: 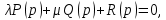 (11.1) (11.1)где Р(р), Q(р), R(р) - многочлены; λ и μ- исследуемые параметры. Граница D-разбиения в плоскости параметров λ и μ определяется уравнением: 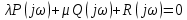 (11.2) (11.2)Полиномы Р(j), Q(j), R(j) могут быть представлены в первой алгебраической форме комплексного числа: 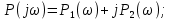 (11.3) (11.3) 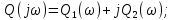 (11.4) (11.4) 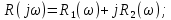 (11.5) (11.5)На основании условия равенства комплексных выражений, которое выполняется тогда и только тогда, когда соответственно равными оказываются действительные и мнимые части, из равенств (11.2-11.5) может быть получена система уравнений: 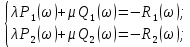 (11.6) (11.6)Система (11.6) является линейной алгебраической системой относительно неизвестных λ и μ, может быть решена различными методами, например, методом Крамера: 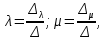 (11.7) (11.7) где Δ; Δλ, Δμ - соответственно главный и вспомогательные определители системы (11.6). Главный определитель Δ рассчитывается на основании коэффициентов при неизвестных в (11.6): 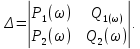 (11.8) (11.8)Вспомогательные определители строятся на основании главного определителя заменой столбца при неизвестной столбцом свободных членов: 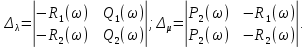 (11.9) (11.9)Граница D-разбиения строится изменением частоты от нуля до бесконечности в координатных осях (λ; μ), причем осью абсцисс является ось параметра, который в (11.2) записан на первом месте (λ), параметр, который записан на втором месте, изображается по оси ординат (μ). Решение системы (11.6) имеет особые случаи, когда главный определитель обращается в ноль. Если при этом вспомогательные определители не равны нулю 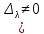 , ,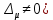 , то (11.7) имеют разрыв второго рода, значения λ и μ стремятся к положительной или отрицательной бесконечности. , то (11.7) имеют разрыв второго рода, значения λ и μ стремятся к положительной или отрицательной бесконечности. Если все определители (главный и вспомогательные) обращаются одновременно в ноль, то на графике есть особые линии, практически они получаются при частоте, равной нулю (=0), или при частоте, стремящейся к бесконечности (→∞). Штриховка границы выполняется с учетом знака главного определителя. Если главный определитель больше нуля (Δ>0), то штриховка выполняется слева от границы при движении в сторону увеличения частоты. Если главный определитель меньше нуля, то штриховка границы выполняется справа при движении в стороны увеличения частоты. Штриховка выполняется двойной, т.к. граница совпадает для положительных и отрицательных частот. Особые линии имеют одинарную штриховку, она должна совпадать с направлением штриховки основных линий вблизи точки сопряжения. Если главный определитель равен нулю не при нулевой частоте, вспомогательные определители равны нулю тоже, то штриховка особой линии выполняется двойная. Если главный определитель равен нулю не при нулевой частоте, но при этом его знак не меняется при переходе через нее, то штриховка особой линии не выполняется, она из рассмотрения удаляется. Пример 11.1.В характеристическом уравнении 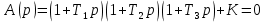 постоянная времени Т1 и коэффициент передачи К могут варьироваться. Определить влияние этих параметров на устойчивость системы. Решение: В характеристическом уравнении выделяются исследуемые параметры: 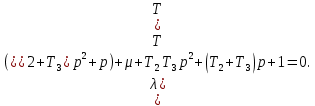 Оператор р заменяется на j: 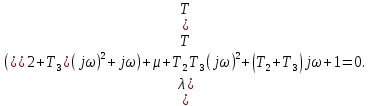 Тогда: 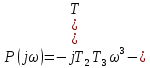 ; ;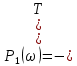 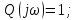 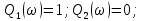 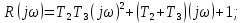 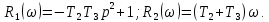 Система уравнений для расчета параметров λ и μ имеет вид: 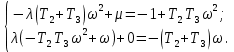 Определители рассчитываются по формулам: 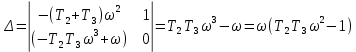 ; ;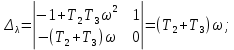 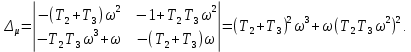 Тогда параметры λ и μ рассчитываются по формулам: 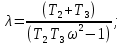 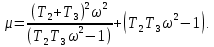 Главный определитель обращается в ноль при частоте, равной 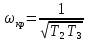 . .Вспомогательные определители при этой частоте не равны нулю, при частоте слева от этого значения ( 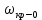 ) параметрλ→-∞, параметр μ→-∞при частоте справа значения параметров ( ) параметрλ→-∞, параметр μ→-∞при частоте справа значения параметров (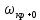 ) λ→+∞; μ→+∞. ) λ→+∞; μ→+∞.При нулевой частоте: 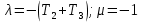 . .При частоте 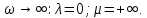 Граница D-разбиения про двум параметрам приведена на рисунке 11.1. 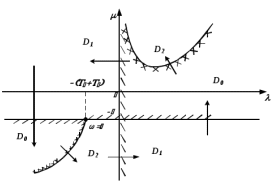 Рисунок 11.1 Граница D-разбиения по двум параметрам Для проверки устойчивости в области с внутренней штриховкой можно принять μ=0; λ>0, тогда характеристическое уравнение примет вид: 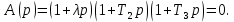 Все корни этого характеристического уравнения отрицательные, следовательно, данная область является областью устойчивости. При движении против двойной штриховки появляются два правых корня, против одинарной штриховки один правый, при пересечении границы по одинарной штриховке особой линии один правый корень меняется на левый, по двойной штриховке два правых корня переходят в левые. После выполнения разметки появляется еще одна область с внутренней штриховкой, в которой нет правых корней, но при этом параметры должны принимать отрицательные значения, что не имеет физического смысла. Система может быть устойчива при любых значениях постоянной времени Т1, если при этом выбирается соответствующее значение коэффициента передачи К из области D0. При больших значениях коэффициента передачи К система может быть устойчива либо при малых значениях постоянной времени, либо при очень больших ее значениях. 11.2 Задания для самостоятельной работы Определить область устойчивости по параметрам Т22и Кр для характеристического уравнения: 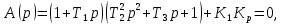 если Т1= 0,06с; Т3 =0,1;К1 = 1. Построить область устойчивости по двум параметрам Т1 иК1методом D-разбиения для системы с характеристическим уравнением 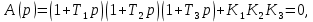 если Т2= 0,1с; Т3 =0,5;К2К3 = 20. 11.3 Вопросы для самопроверки Какие линейные системы считаются устойчивыми, неустойчивыми, безразлично устойчивыми? Как построить характеристическое уравнение по известной передаточной функции? Как из характеристического уравнения получить функцию Михайлова? Какое свойство комплексных чисел позволяет получить систему линейных алгебраических уравнений относительно исследуемых параметров? Как по методу Крамера можно рассчитать параметры? Как строится главный определитель для системы алгебраических уравнений, построенной для исследуемых параметров? Как из главного определителя получить вспомогательные определители? Каким образом отражается на виде границы устойчивости равенство нулю главного определителя? Особенности выполнения штриховки при использовании метода D-разбиения по двум параметрам. Особые линии, как их определить и выполнить штриховку. Как определить область возможной устойчивости системы, как это проверить? Как по полученному графику D-разбиения определить области с появлением правых корней? В области с внутренней штриховкой система оказалась неустойчивой, можно ли изменением исследуемых параметров добиться устойчивости системы? На графике D-разбиения есть область с внутренней штриховкой, проверка показала, что система будет устойчива, но параметры при этом принимают отрицательные значений, какой вывод можно сделать об области изменения исследуемых параметров. 12 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ НА ТЕМУ «ОЦЕНКА КАЧЕСТВА УПРАВЛЕНИЯ В УСТАНОВИВШИХСЯ РЕЖИМАХ» Цель практического занятия: Получение навыков расчета показателей качества управления в линейных непрерывных системах в установившихся режимах. 12.1 Теоретические сведения Качество управления САУ – совокупность свойств САУ, обеспечивающих эффективное функционирование системы в целом, характеризующих точность поддержания управляемой величины на заданном уровне в установившихся и переходных режимах. В свою очередь, свойства, из этой совокупности, выраженные в количественной форме, называются показателями качества управления САУ. Качество управления в установившемся режиме оценивается величиной ошибки управления 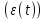 , т.е. разностью между заданным , т.е. разностью между заданным 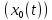 и фактическим значением и фактическим значением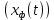 , эта разность должна принимать как можно меньшее значение (12.1): , эта разность должна принимать как можно меньшее значение (12.1):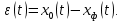 (12.1) (12.1)Изображение ошибки можно вычислить по известной передаточной функции системы. Так, если система имеет структурную схему (рисунок 12.1),то изображение ошибки имеет вид (12.2): 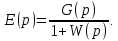 (12.2) (12.2) Рисунок 12.1 – Структурная схема исследуемой системы Передаточная функция системы W(p) в общем виде может быть представлена в виде (12.3): 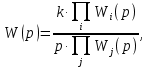 (12.3) (12.3)где 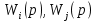 – передаточные функции элементарных звеньев, записанные в стандартной форме, т.е. свободный член равен единице. – передаточные функции элементарных звеньев, записанные в стандартной форме, т.е. свободный член равен единице.Если в прямой цепи нет интегрирующих звеньев, то 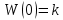 , тогда изображение ошибки имеет вид (12.4): , тогда изображение ошибки имеет вид (12.4):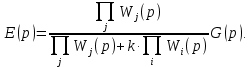 (12.4) (12.4)Если задающее воздействие имеет постоянное значение 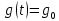 , то его изображение имеет вид (12.5): , то его изображение имеет вид (12.5):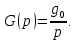 (12.5) (12.5)Тогда изображение ошибки (12.4) примет вид (12.6): 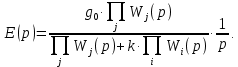 (12.6) (12.6)На основании свойств преобразования Лапласа (теорема о предельном значении): 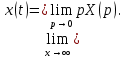 (12.6) (12.6)Значение ошибки при 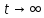 : :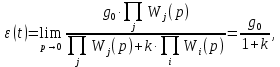 (12.7) (12.7)т.е. при отсутствии интегрирующих звеньев в установившемся режиме всегда присутствует ошибка. Её величина тем больше, чем меньше К. В астатической системе, в которой есть интегральные звенья, при 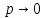 : :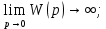 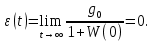 (12.8) (12.8)Ошибки в установившемся режиме можно рассчитать с помощью коэффициентов ошибок, для этого изображение ошибки раскладывается в ряд: 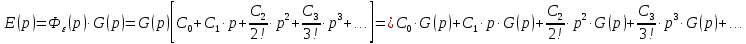 с другой стороны: 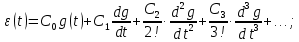 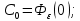 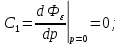 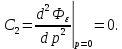 Чтобы найти коэффициенты ошибок Сi, можно воспользоваться правилом деления многочленов. Если передаточная функция разомкнутой системы имеет вид: 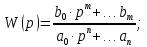 (12.9) (12.9)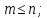 то передаточная функция по ошибке: то передаточная функция по ошибке: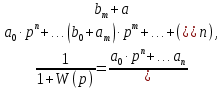 (12.10) (12.10)тогда: 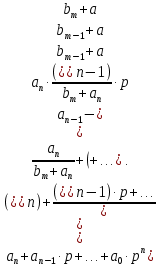 Для статических систем: 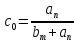 – коэффициент статической ошибки (позиционной); – коэффициент статической ошибки (позиционной);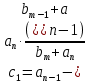 – коэффициент статической ошибки по скорости и т.д. – коэффициент статической ошибки по скорости и т.д.Для астатических систем 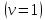 : :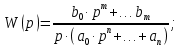 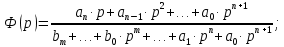 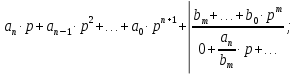 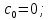 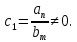 Для этой системы позиционная ошибка равна нулю, а скоростная ошибка определяется коэффициентом 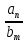 . . |
