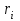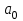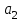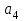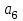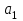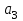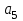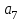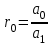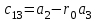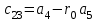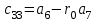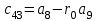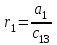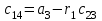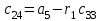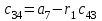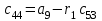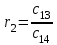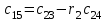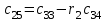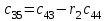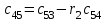Учебное пособие по дисциплине Теория автоматического управления для студентов направлений
 Скачать 2.41 Mb. Скачать 2.41 Mb.
|
|
6.5 Критерий Рауса Система устойчива, если в первом столбце таблицы Рауса все коэффициенты положительны (таблица 6.1). Таблица 6.1 Таблица для расчета коэффициентов Рауса
Замечание. Если среди ri есть отрицательные, то система неустойчива, характеристическое уравнение имеет правые корни, при этом их число равно числу перемен знака в столбце ri.. 6.6Расчет критических значений параметров системы Критерий Гурвица может использоваться для расчета критического значения параметра, соответствующего границе устойчивости. Для этого определитель (n-1)-ого порядка нужно приравнять нулю и разрешить относительно интересующего параметра. Решение полученного уравнения определяет критическое значение параметра. Пример 6.4. Характеристическое уравнение имеет вид: 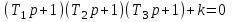 , ,найти критическое значение коэффициента усиления при заданных значениях постоянных времени 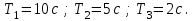 Решение:После раскрытия скобок характеристического уравнения: 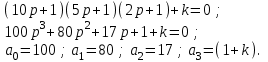 Определитель Гурвица имеет вид: 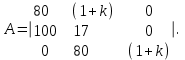 Необходимое условие устойчивости системы: 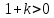 . .Для устойчивости системы нужно, чтобы определитель 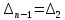 был положительным, т.е. был положительным, т.е.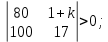 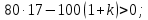 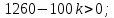 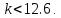 Таким образом, коэффициент усиления не должен превышать этого значения. 6.7 Задания для самостоятельного решения 6.7.1 Определить устойчивость системы по теореме Ляпунова, по критерию Гурвица и по критерию Рауса, если её характеристическое уравнение имеет вид: 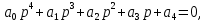 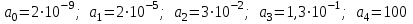 ; ;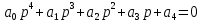 , ,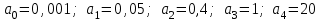 ; ;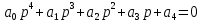 , ,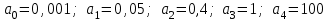 ; ;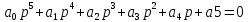 , ,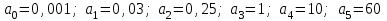 ; ;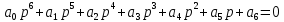 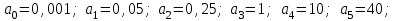 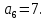 6.7.2Для системы с единичной обратной связью и известной передаточной функцией прямой цепи построить область устойчивости, используя критерий Гурвица, по незаданному параметру Т2, если k= 3,5, Т1 = 0,2 с. 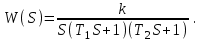 6.8 Вопросы для самопроверки Какие линейные системы считаются устойчивыми, неустойчивыми, безразлично устойчивыми? Что такое характеристическое уравнение? Из каких составляющих можно представить вектор состояния по Ляпунову? Чем определяется свободная составляющая вектора состояния? При каких условиях вынужденная составляющая может быть равна вектору состояния? Приведите примеры корней характеристического уравнения, соответствующих трем возможным состояниям линейной системы по устойчивости. Приведите примеры, когда можно уверенно сказать, что система неустойчива. Сформулируйте критерий Гурвица, приведите вид главного определителя для характеристического уравнения четвертого порядка. Какой вывод можно сделать об устойчивости системы, если все определители низших порядков положительны, а (n-1)-ого порядка равен нулю? Что можно определить в этом случае? Можно ли по критерию Гурвица определить количество правых корней характеристического уравнения? Как по таблице Рауса можно определить, что система неустойчива? Какой алгебраический критерий позволяет определить число правых корней характеристического уравнения? 7 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ НА ТЕМУ «КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА» Цель практического занятия: Применение критерия Михайлова для исследования устойчивости линейных систем. 7.1 Основные теоретические сведения Критерий Михайлова использует свойства комплексных чисел, исследуя устойчивость системы, заданной передаточной функцией: W(p)=B(p)/D(p).(7.1) Для этого записывается характеристический полином, т.е. знаменатель передаточной функции D(p). Если в нем заменить оператор р=j, то полученное выражение называется функцией Михайлова (D(j)), а ее график, полученный при изменении частоты от нуля до бесконечности, годографом Михайлова. Любой полином согласно теореме Безу может быть представлен в виде произведения одночленов вида (p-pi), где pi – корень соответствующего ему уравнения. Таким образом, функция Михайлова по этой теореме имеет вид: 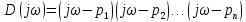 , (7.2) , (7.2)где n- порядок функции. Комплексная функция, имеющая вид произведения комплексных выражений, имеет модуль, равный произведению модулей, и аргумент, равный сумме аргументов. Аргумент каждой скобки зависит от изменения частоты и от вида корня, имеющего либо положительную, либо отрицательную действительную часть. Так если корень имеет отрицательную действительную часть (его называют левым), то скобка 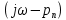 на комплексной плоскости имеет изображение, приведенное на рисунке 7.1. на комплексной плоскости имеет изображение, приведенное на рисунке 7.1.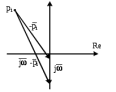 Рисунок 7.1 – Изображение на комплексной плоскости ( 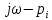 ) в случае левого корня ) в случае левого корняПри изменении частоты от минус бесконечности до плюс бесконечности вектор ( 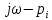 ) сделает поворот против часовой стрелки на 180° (или ) сделает поворот против часовой стрелки на 180° (или 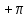 ). ).Если корень правый, то векторное представление ( 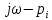 )на комплексной плоскости имеет вид (рисунок 7.2). )на комплексной плоскости имеет вид (рисунок 7.2).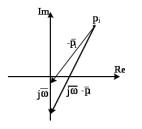 Рисунок 7.2 – Изображение разности ( 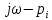 )для правого корня )для правого корняВ этом случае при изменении частоты от минус бесконечности до плюс бесконечности вектор ( 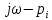 )будет вращаться по часовой стрелке и пройдет угол )будет вращаться по часовой стрелке и пройдет угол 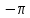 . .Если система устойчива, т.е. все корни левые (с отрицательными действительными частями), то суммарный поворот годографа при изменении частоты от минус бесконечности до плюс бесконечности составит 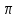 n, где n - степень характеристического полинома. n, где n - степень характеристического полинома.Если есть правые корни, допустим m правых корней, тогда левых корней останется (n - m). Годограф при изменении частоты от минус бесконечности до плюс бесконечности будет иметь суммарный поворот 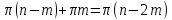 , т.е. будет меньше , т.е. будет меньше 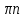 . .Реальное изменение частоты обычно принадлежит интервалу от нуля до бесконечности. Поэтому изменение аргумента каждой скобки будет равно либо +90°, либо –90°. На основании этих свойств комплексных чисел критерий Михайлова может быть сформулирован следующим образом. Линейная непрерывная система устойчива, если при изменении частоты от нуля до бесконечности годограф Михайлова, начинаясь на действительной положительной полуоси ( 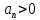 по необходимому критерию устойчивости), проходит в положительной направлении (против часовой стрелки) последовательно и нигде не обращаясь в ноль, столько четвертей, какова степень характеристического уравнения. по необходимому критерию устойчивости), проходит в положительной направлении (против часовой стрелки) последовательно и нигде не обращаясь в ноль, столько четвертей, какова степень характеристического уравнения.Схематично годографы Михайлова, соответствующие устойчивым системам, приведены на рисунке 7.3. 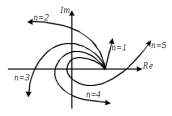 Рисунок 7.3 – Общий вид годографов Михайлова, соответствующих устойчивым системам На рисунке 7.4 приведены примеры годографов для неустойчивых систем. 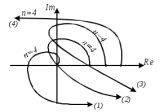 Рисунок 7.4 – Примеры годографов для неустойчивых систем: 1 – начинается в точке (0;0); 2 – проходит через точку (0;0); 3 – нарушен порядок обхода четвертей; 4 –число четвертей меньше порядка характеристического уравнения Построение годографа прямым изменением частоты бывает не всегда оптимально, поэтому можно воспользоваться особенностями пересечения годографом координатных осей (они при увеличении частоты должны пересекаться последовательно, сначала мнимая ось при положительном значении, затем действительная полуось, затем мнимая отрицательная и т.д.). Поэтому для схематического построения годографа можно использовать следующий алгоритм: записать характеристический полином D(p); заменить оператор р=j; представить функцию Михайлова в первой алгебраической форме: 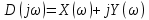 ; ;приравнять мнимую часть нулю 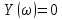 , найти корни и полученные значения подставить в действительную часть, тем самым определить точки пересечения с действительной полуосью; , найти корни и полученные значения подставить в действительную часть, тем самым определить точки пересечения с действительной полуосью;приравнять действительную часть нулю, найти корни подставить их в мнимую часть, тем самым определить точки пересечения с мнимой осью; в соответствии с увеличением частоты нанести точки пересечения осей (схематично); по виду получившегося годографа сделать вывод об устойчивости системы. Пример 7.1. Исследовать устойчивость системы, если ее характеристический полином имеет вид: 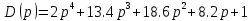 . .Решение:Создается функция Михайлова, записывается в первой алгебраической форме: 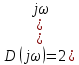 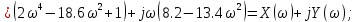 Находятся корни мнимой части: Y() = (8,2 – 13,4 2) = 0; 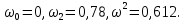 Определяются точки пересечения с действительной полуосью: 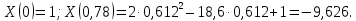 Корни действительной части определяются из уравнения: 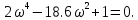 Они равны =3,0407; =0,2325; точки пересечения с мнимой осью: 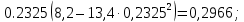 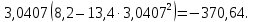 При частоте, стремящейся к бесконечности, действительная часть стремится к плюс бесконечности, мнимая часть к минус бесконечности. Схематичное изображение годографа Михайлова приведено на рисунке 7.5. Годограф начинается на действительной положительной полуоси, при увеличении частоты движется против часовой стрелки, проходит четыре четверти, следовательно, исследуемая система устойчива. Информацию можно представить в виде таблицы (таблица 7.1). Таблица 7.1 Результаты расчета особых точек годографа Михайлова
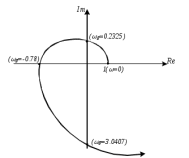 Рисунок 7.5 – Схематичное изображение годографа Михайлова По таблице 7.1 можно сделать вывод об устойчивости системы, т.к. при = 0Х()-положительна; нулевые значения действительной и мнимой частей чередуются при возрастании частоты. Вместо годографа на комплексной плоскости можно строить зависимости действительной и мнимой частей функции Михайлова от частоты на одном графике в декартовой системе координат (рисунок 7.6). 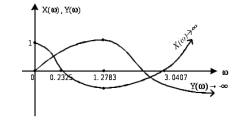 Рисунок 7.6 – Третий вариант иллюстрации критерия Михайлова Действительная часть для устойчивой системы должна начинаться при частоте равной нулю в положительной ординате, мнимая часть в нуле; с увеличением частоты функции пересекают ось частот по очереди, при частоте, стремящейся к бесконечности, для данного примера действительная часть положительна, мнимая отрицательна, таким образом можно сделать вывод, что исследуемая система устойчива. Критерий Михайлова можно использовать для определения критического значения параметра, соответствующего границе устойчивости системы. Для этого необходимо приравнять функцию Михайлова нулю, найти значения частоты, при которой мнимая часть равна нулю, и подставить это значение в действительную часть. Из получившегося уравнения находится критическое значение параметра. Пример 7.2. Определить критическое значение коэффициента передачи Кр, соответствующего границе устойчивости системы, заданной характеристическим уравнением: 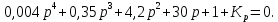 Решение: Функция Михайлова получается заменой p = j: 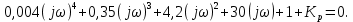 Действительная часть: 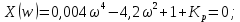 мнимая часть: 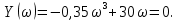 Корни мнимой части: 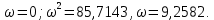 При подстановке в действительную часть: 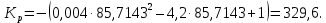 Коэффициент передачи, при котором система находится на границе устойчивости, равен 326,9. При дальнейшем увеличении Кр система станет неустойчивой. |