Исследование систем управления организациями. Учебное пособие по курсу Исследование систем управления для студентов

• Название: Учебное пособие по курсу Исследование систем управления для студентов
• Анкор: Исследование систем управления организациями.doc
• Дата: 22.12.2017
• Размер: 0.96 Mb.
• Имя файла: Исследование систем управления организациями.doc
• Тип: Учебное пособие; #12537
• Категория: Электротехника. Связь. Автоматика
• страница: 10 из 24

Исследование устойчивости плановых решений

При использовании детерминированной модели линейного программирования (5.1), (5.2) для определения планов выпуска продукции или оказания услуг для реальных предприятий координаты векторов c, b и элементы матрицы A считаются детерминированными величинами, хотя в реальности они имеют интервальную неопределенность:

c_i[ c_{i min}, c_{i max}], ; (5.3)

a_ij[ a_{ij min}, a_{ij max}], , ; (5.4)

b_i[ b_{i min}, b_{i max}], . (5.5)
Полученные плановые решения по детерминированной однокритериальной модели линейного программирования (5.1), (5.2) далеки от реальных оптимальных решений, так как не учтены интервальные неопределенности параметров (5.3) – (5.5). С учетом интервальной неопределенности параметров целевой функции (5.3) и параметров ограничений (5.4), (5.5) задача определения оптимального реального плана имеет вид: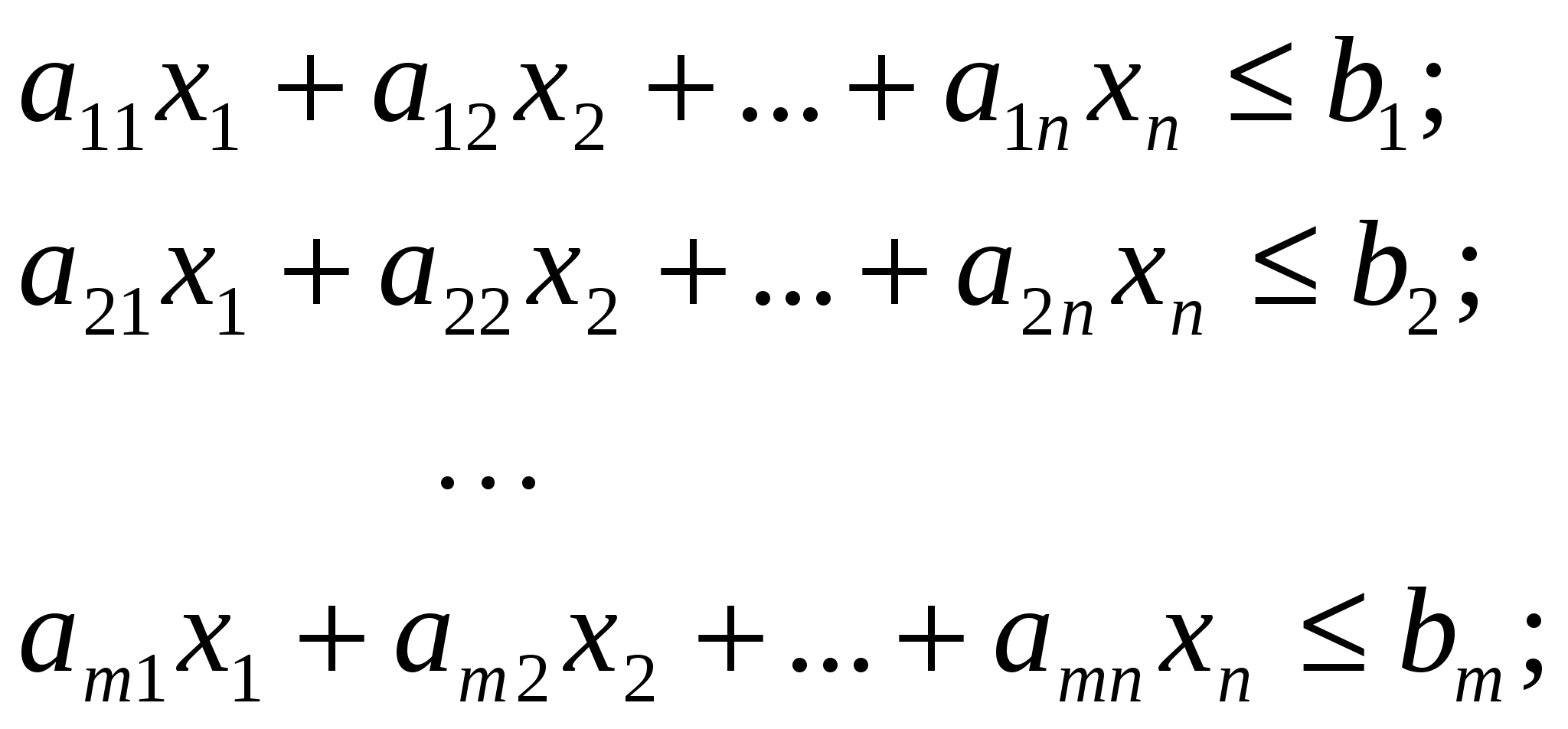

; (5.6)

(5.7)

(5.8)

, ; (5.9)

, , ; (5.10)

, . (5.11)

Для наглядности представления области решения с использованием графического метода рассмотрим задачу (5.3) – (5.11) при n=2. В этом случае задача планирования должна быть представлена в виде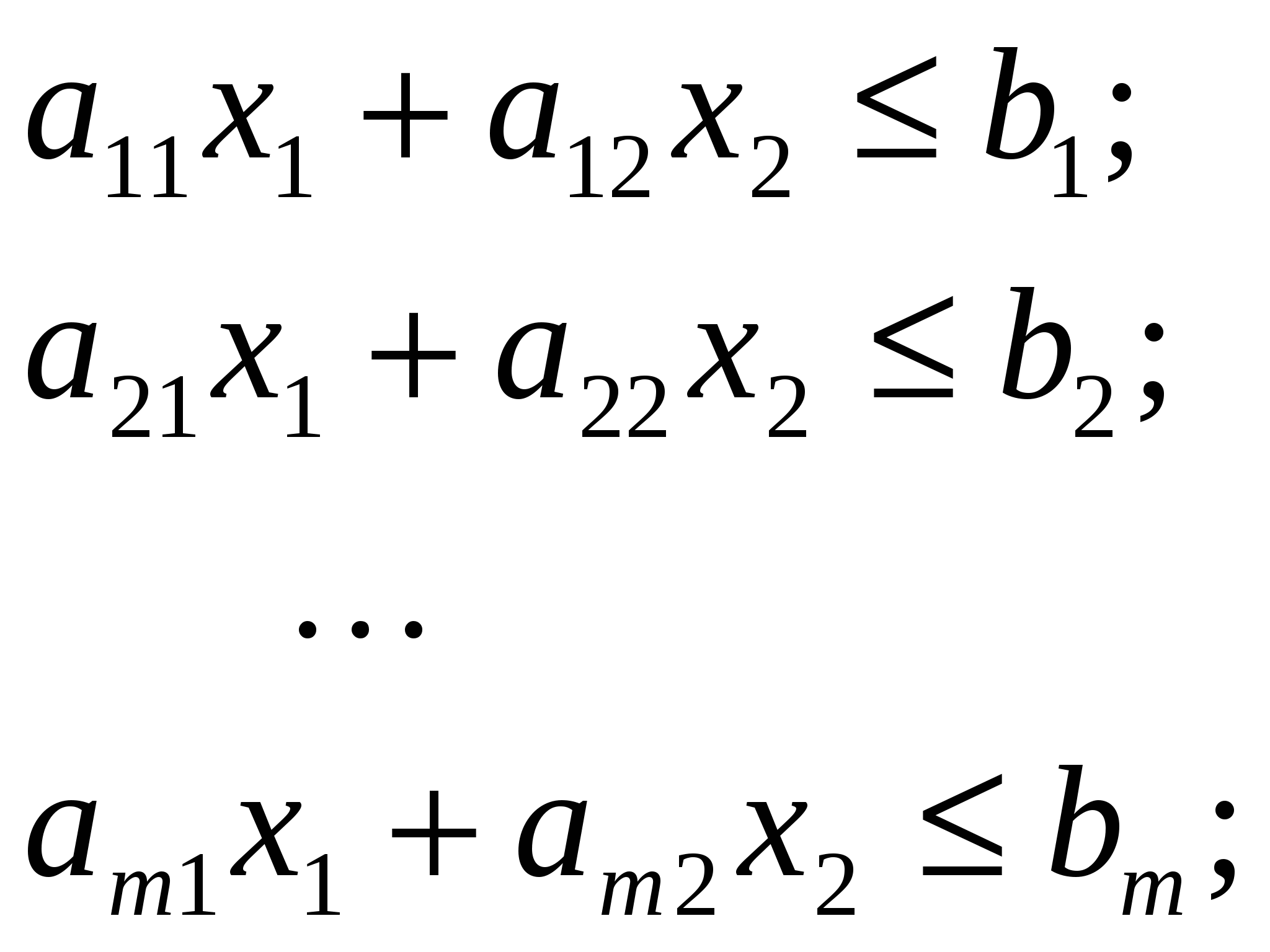

; (5.12)

(5.13)

; (5.14)

, ; (5.15)

, , ; (5.16)

, . (5.17)
При исследовании устойчивости решения исходной задачи (5.12) – (5.14) необходимо рассмотреть последовательно влияние неопределенностей параметров (5.12) – (5.14).

Сначала рассмотрим влияние интервалов неопределенности параметров c_i на устойчивость решения исходной задачи (5.12) – (5.14)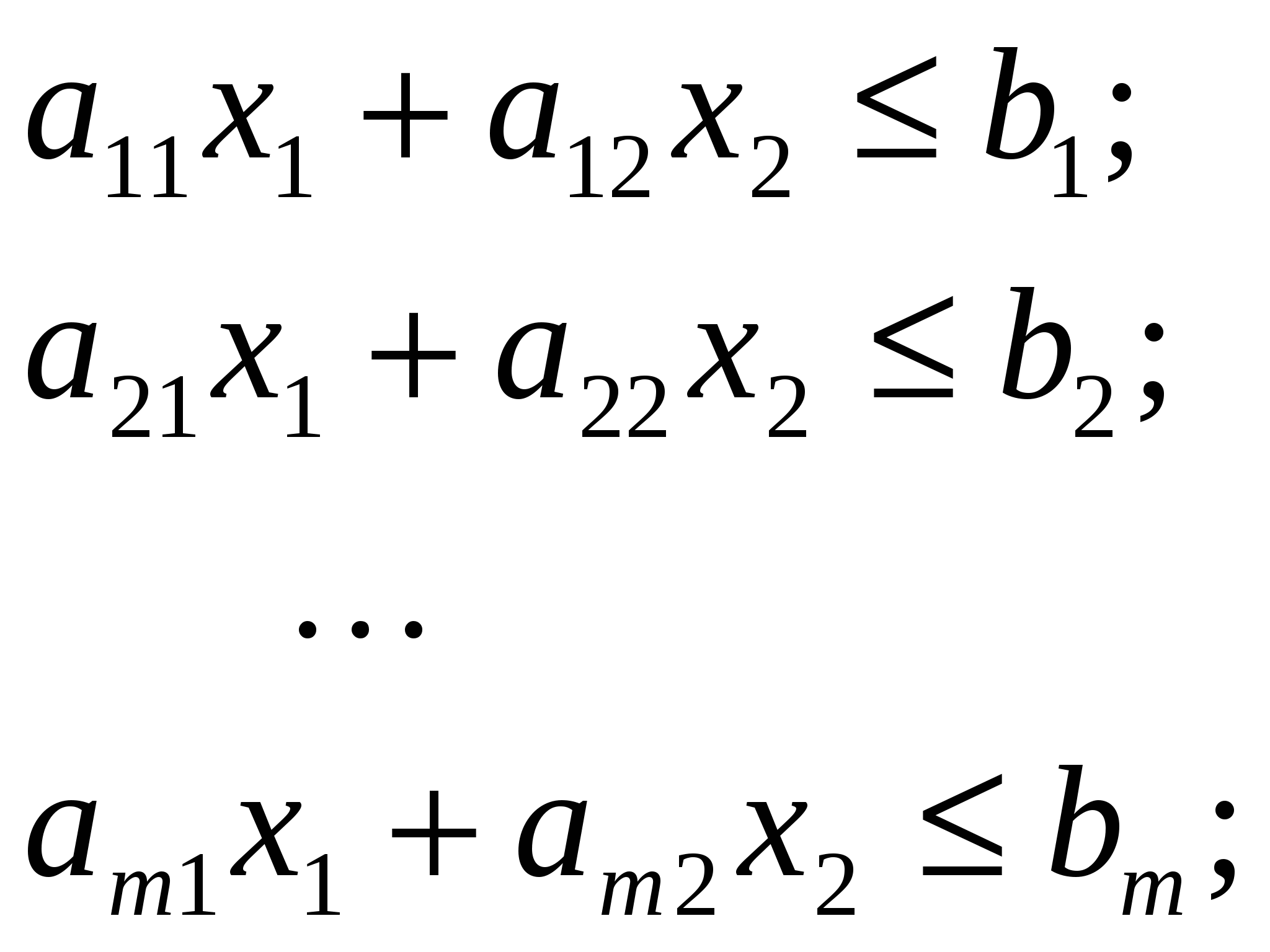

;



;

, .

При проверке на устойчивость мы должны перейти к многокритериальной задаче линейного программирования, где частные критерии оптимальности определяются «конусом критериев», внутри которого находится n-мерный куб C, координаты которого определяются условием (5.3), а допустимая область S определяется условиями (5.7), (5.8). При n=2 решается двукритериальная задача

; (5.18)

; (5.19)

,

где S – допустимая область решений, задаваемая ограничениями (5.13), (5.14).

Графическая иллюстрация допустимой области решения S, градиентов функций f, f₁, f₂ и области изменений С градиента целевой функции f приведена на рис. 5.4.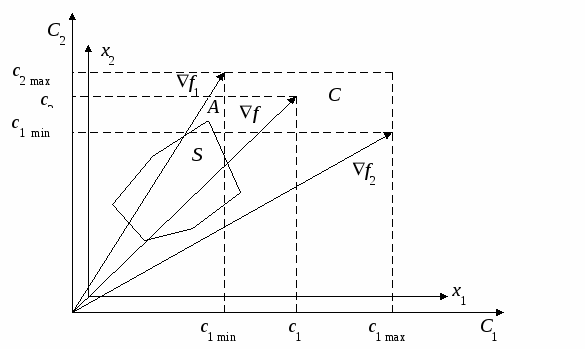

Рис. 5.4
При определении устойчивости необходимо использовать следующее правило:

Решение исходной задачи (5.12) – (5.14) устойчиво, если оно совпадает с решением многокритериальной задачи (5.18), (5.19), в противном случае решение неустойчиво при интервальной неопределенности .
Пример 3.

Определение устойчивости решений для задачи оптимального планирования, приведенной в примере 2.

f = 0,25x₁ + 0,3x₂max;

x₁ + x₂ 100;

x₁ ≥ 50;

x₂≥ 10;

x₁  0; х₂  0.
;

;

c_{1 min} =0,15

c_{1 max} =0,35

c_{2 min} =0,2

c_{2 max} =0,4
f₁= 0,15x₁ + 0,4x₂max,

f₂= 0,35x₁ + 0,2x₂ max,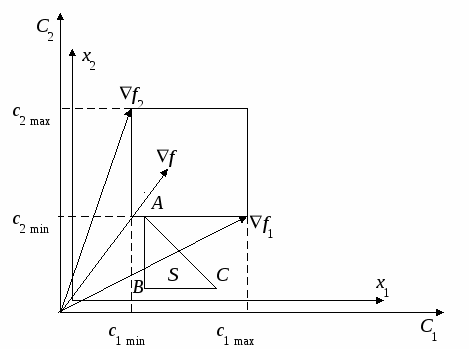




Рис.5.5.
Решение исходной задачи неустойчиво, так как решение двукритериальной задачи не совпадает с решением исходной задачи.
При интервальной неопределенности параметров (5.16) модель задачи оптимального планирования имеет вид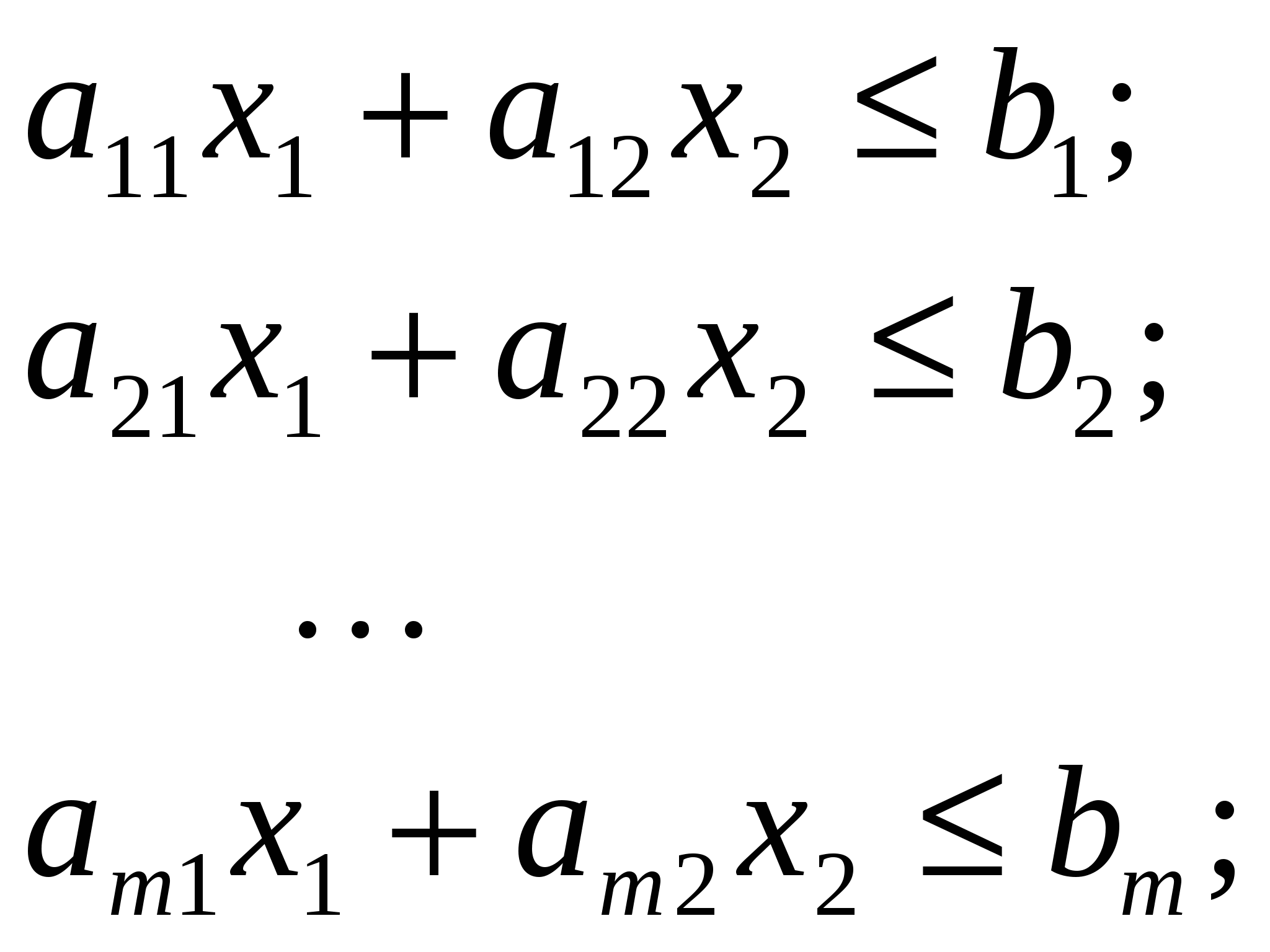

;

.13)

(5.14)

, , . (5.16)

Допустимая область решений, представляющая собой многогранник, деформируется. Один из возможных вариантов деформации допустимого множества показан на рис. 5.6.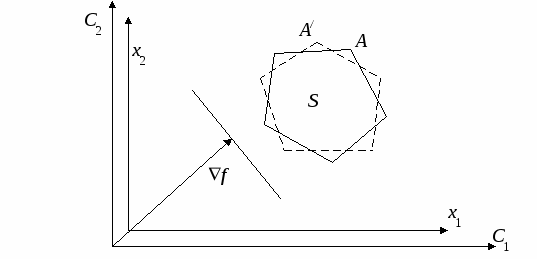



Рис. 5.6
При интервальной неопределенности параметров (5.16) решение исходной задачи (5.12) – (5.14) неустойчиво.

При интервальной неопределенности параметров (5.17) модель задачи оптимального планирования имеет вид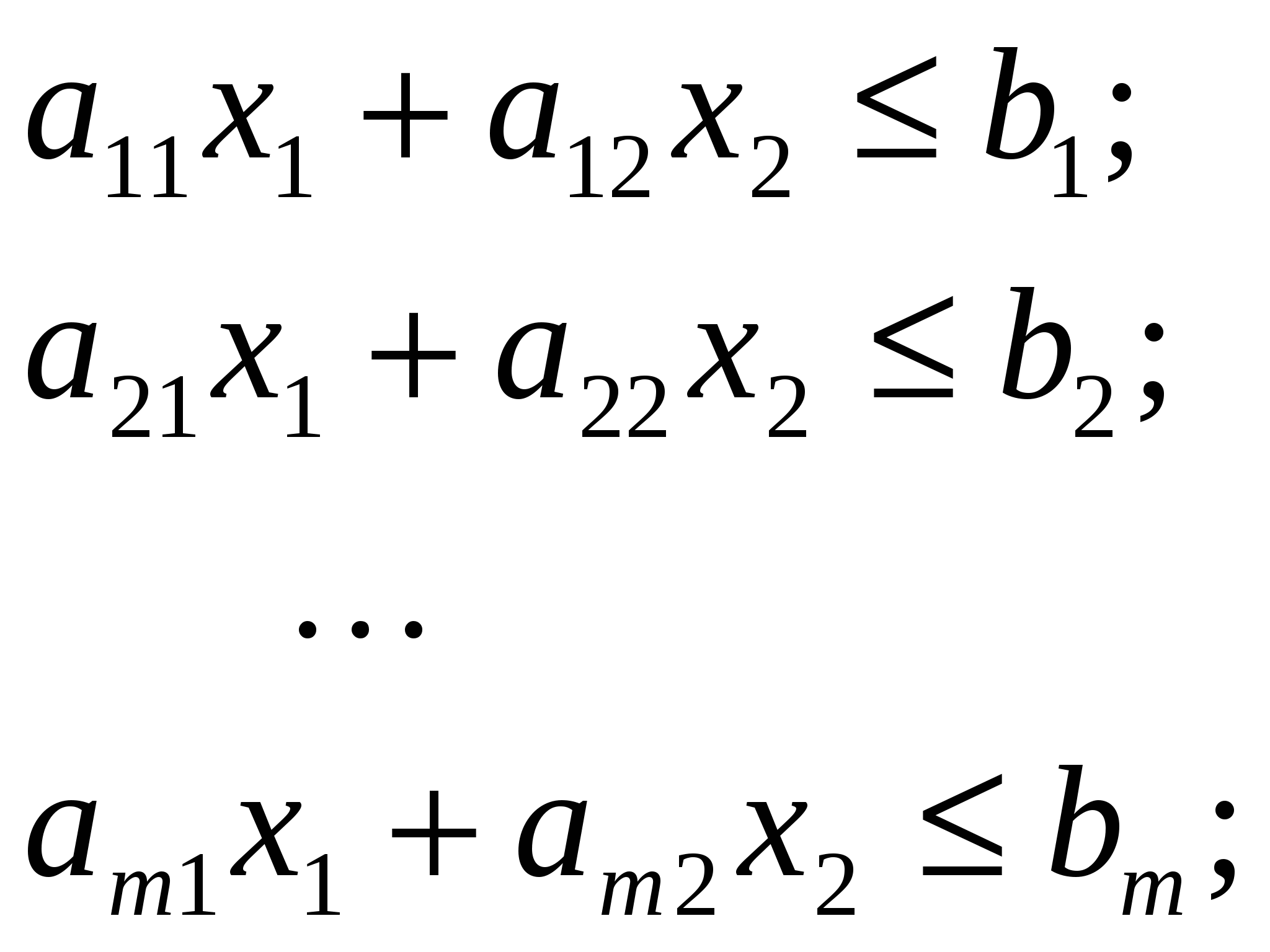







,

Допустимая область решений, представляющая собой многогранник, деформируется. Один из возможных вариантов деформации допустимого множества показан на рис. 5.7.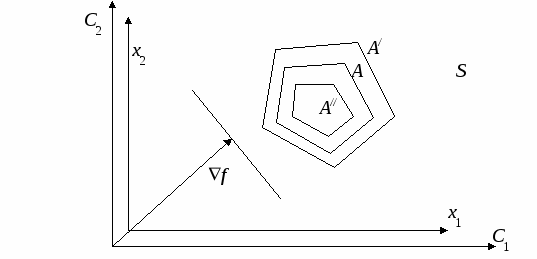



Рис. 5.7
При интервальной неопределенности параметров (5.17) решение исходной задачи (5.12) – (5.14) неустойчиво.

При интервальной неопределенности одновременно параметров, представленных формулами (5.15), (5.16) или (5.15), (5.17) решение исходной задачи (5.12) – (5.14) неустойчиво.

5.1.3. Многокритериальное оптимальное планирование

Большинство задач планирования в реальных организационных системах носит многокритериальный характер и может быть представлено задачей многокритериального линейного программирования в виде: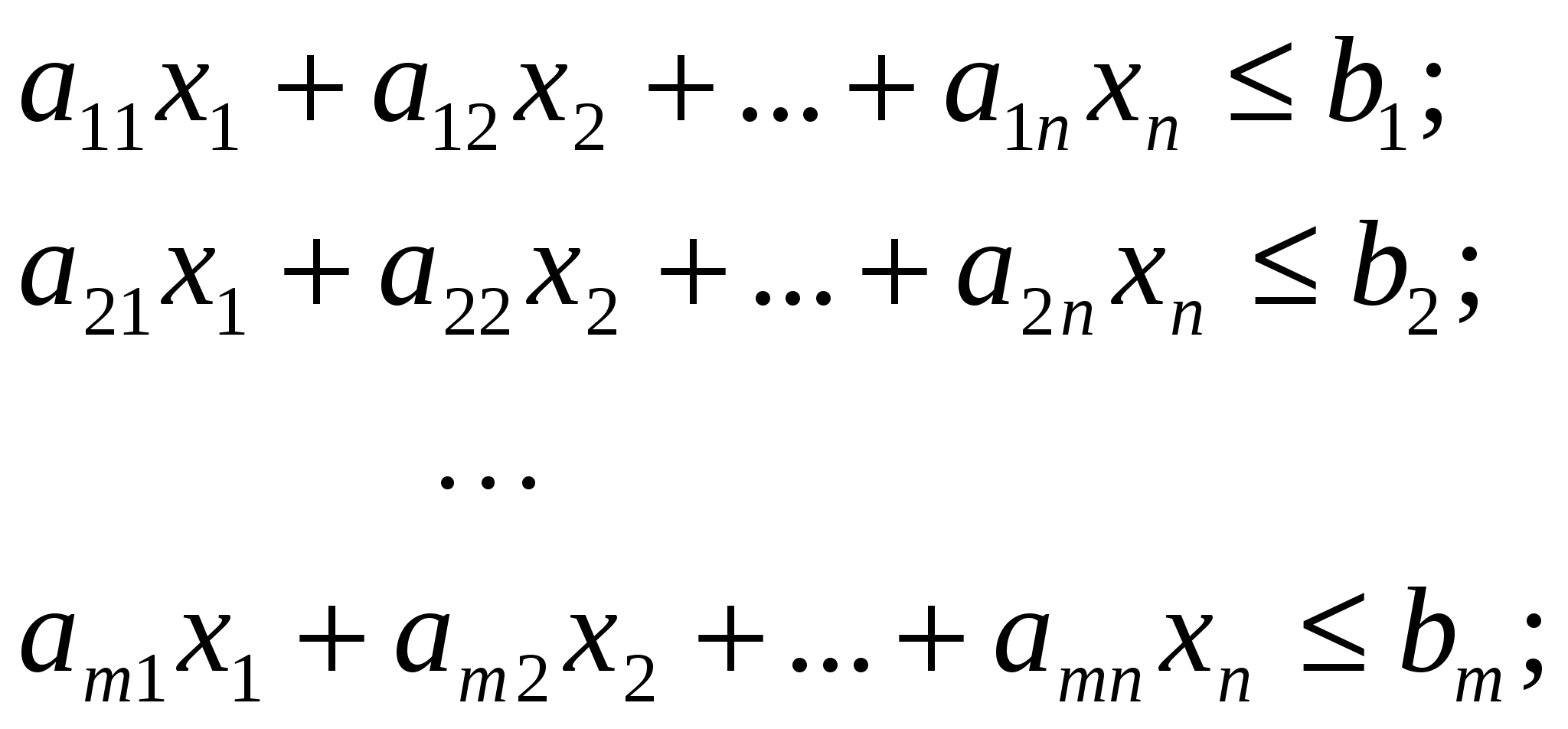

, ; (5.20)

(5.21)

(5.22)

, ; (5.23)

, , ; (5.24)

, , (5.25)

где f_l– частный критерий оптимальности;

L – количество частных критериев оптимальности;

– коэффициенты частного критерия оптимальности , ;

b_j– запасы j-го вида ресурса, предназначенного для выполнения оптимального плана, ;

a_ij- расход j-ого ресурса на выпуск единицы i-го вида продукта.

С методами решения детерминированных задач многокритериальной оптимизации, определяемых условиями (5.20) – (5.22), можно ознакомиться в [14].

Графическое представление задачи многокритериального линейного программирования показано на рис. 5.8.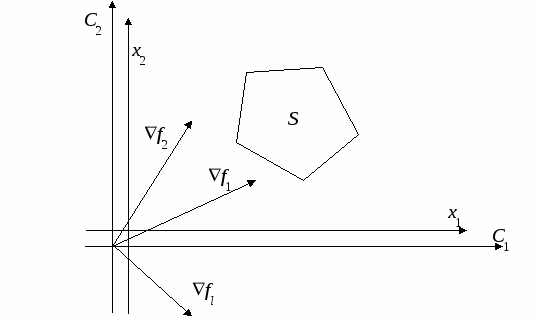


Рис. 5.8

Методика определения решений многокритериальной задачи оптимизации в условиях неопределенности (5.20) – (5.25) представлена в [14].

Для иллюстрации определения области решений напомним о некоторых определениях, данных в [14], и рассмотрим практический пример.

Определение 1.

Из двух точек точка называется доминирующей по отношению к (), если для всех выполняется и, кроме того, по крайней мере, для одного j .

Определение 2.

Точка называется улучшаемой, если существует хотя бы одна точка , такая, что , и хотя бы для одного j: , в противном случае точка не улучшаемая или эффективная.

Определение 3.

Множество S₁, состоящее из эффективных точек, называется множеством решений, оптимальных по Парето.

Для определения области Парето необходимо использовать следующее правило [14]:

если все вектора, указывающие направления улучшения критериев (направление улучшения критерия совпадает с направлением градиента функции , если , и с направлением антиградиента функции , если ) принадлежат открытой полуплоскости, проведенной через начало координат в системе координат (с₁, с₂), то решением многокритериальной задачи оптимизации (5.20) – (5.22) является область Парето, представляющая часть границы допустимой области решений, в противном случае областью решений многокритериальной задачи будет вся допустимая область.

Пример 3.

Банк имеет возможность инвестировать финансовые ресурсы в размере 10 млн долларов в два проекта. При инвестировании в первый проект прибыль составляет 30% годовых, при инвестировании во второй проект - 35% годовых. Потери от риска при вложении в первый проект составляют 6% годовых, во второй проект – 6,5% годовых. Какое количество финансовых средств банк должен вложить в первый и во второй проекты, чтобы получить максимальную прибыль и обеспечить минимальные потери от риска?

f₁ = 0,3x₁ + 0,35x₂max;

f₂ = 0,06x₁ + 0,065 x₂  min;

x₁ + x₂  10;

x₁ > 0; х₂ > 0.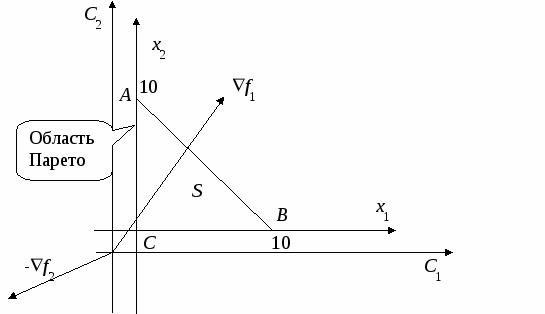


Рис. 5.9
Решением задачи по критерию f₁ max является точка А, решением задачи по критерию f₂minявляется точка С. Решением двукритериальной задачи будет отрезок прямой АС, представляющий собой множество Парето.

Определение устойчивости оптимальных плановых решений при использовании детерминированной модели многокритериального линейного программирования вида (5.20) – (5.22) при интервальной неопределенности параметров может быть проведено с использованием методов, указанных в [14].