Исследование систем управления организациями. Учебное пособие по курсу Исследование систем управления для студентов

• Название: Учебное пособие по курсу Исследование систем управления для студентов
• Анкор: Исследование систем управления организациями.doc
• Дата: 22.12.2017
• Размер: 0.96 Mb.
• Имя файла: Исследование систем управления организациями.doc
• Тип: Учебное пособие; #12537
• Категория: Электротехника. Связь. Автоматика
• страница: 9 из 24

Классификация планирования

Планирование классифицируется по следующим критериям.

1. 
   Период планирования:
   
   1. 
      стратегическое (долгосрочное);
      
   2. 
      тактическое (среднесрочное);
      
   3. 
      оперативное (краткосрочное).
      
2. 
   Уровень планирования:
   

1. 
   организация в целом;
   
2. 
   подразделение;
   
3. 
   проект;
   

3. 
   Предмет планирования:
   

1. 
   НИОКР;
   
2. 
   производство;
   
3. 
   снабжение;
   
4. 
   сбыт;
   
5. 
   маркетинг;
   
6. 
   персонал;
   
7. 
   финансы.
   

4. 
   Содержание планирования:
   

1. 
   продуктово-тематическое;
   
2. 
   технико-экономическое;
   
3. 
   объемно-календарное.
   

5. 
   Качество планирования:
   

1. 
   оптимальное планирование, которое подразделяется:
   

• 
  однокритериальное планирование;
  
• 
  многокритериальное планирование;
  
• 
  планирование в условиях неопределенности;
  

2. 
   удовлетворительное планирование;
   
3. 
   абсолютно гарантированное планирование.
   

Содержательный аспект в планировании находит свое выражение в трех видах плановых рас­четов: продуктово-тематическом, технико-экономическом и объемно-кален­дарном.

Продуктово-тематическое планирование заключается в формировании перспективных направлений и тематики НИОКР, подготовке программ и мероприятий по обновлению и выпуску продукции, совершенствованию технологии и организации производства на предприятии. Этот вид планирования предусматривает разработку и оптимизацию производственных программ предприятия и отдельных подразделений.

Технико-экономическое планирование включает расчеты материальных, трудовых и финансовых ресурсов, необходимых для выполнения номенклатурно-тематических заданий, а также оценку экономических результатов и эф­фективности деятельности предприятия. Этот вид расчетов включает финансовое планирование, составление бизнес-планов, бюджетное планирова­ние и т.п.

Объемно-календарное планирование заключается в планирова­нии объемов работ, загрузки подразделений и исполнителей; построении ка­лендарных графиков проведения работ по отдельным проектам, всей совокуп­ности планируемых работ, загрузки оборудования и исполнителей; распреде­лении работ по отдельным календарным периодам.

Состав и сочетание различных видов планов в рамках отдельной организа­ции формируются исходя из принятой в ней концепции планирования ее деятельности.

5.1.2. Оптимальное планирование

(однокритериальная модель)

Пример 1. Предприятие выпускает n видов изделий. Известна величина прибыли, которая может быть получена от реализации единицы i-го вида продукции. Известен расход j-го вида ресурса (финансовые, материальные, трудовые ресурсы) на выпуск единицы i-го вида продукции. Известны выделенные объемы каждого из видов ресурсов. Необходимо определить, какое количество i-го вида изделий нужно выпустить и реализовать в течение года с целью получения максимальной прибыли.

Пример 2. Банк имеет возможность инвестировать финансовые ресурсы в размере 100 млн долларов в два проекта. При инвестировании в первый проект прибыль составляет 25% годовых, при инвестировании во второй проект – 30% годовых. Для обеспечения ликвидности в 1-ый проект должно быть инвестировано не менее 50% имеющихся средств. Учитывая налоговую политику, во второй проект должно быть вложено не менее 10% имеющихся средств. Определить, какое количество финансовых средств должно быть вложено в 1-ый и 2-ой проекты с целью получения максимальной прибыли.

Для каждого из этих примеров модель планирования может быть описана детерминированной моделью линейного программирования [13]:

f = (c, x) → min, (5.1)

xS, S = {xRⁿ: = b, x≥0}, (5.2)

где

с – вектор размерности n, cRⁿ;

A– матрица размера m×n ранга m,

b – вектор размерности m, bRⁿ;

S – допустимое множество решений.

Методы решения задач линейного программирования приведены в прилож. 1.

Математическая модель задачи для примера 2 выглядит следующим образом:

f = 0,25x₁ + 0,3x₂max

x₁ + x₂ 100

x₁ ≥ 50

x₂≥ 10

x₁ 0; х₂ 0
Количество переменных в данной задаче n = 2. Можно использовать графический метод решения задачи линейного программирования. Допустимая область решений S и направление градиента 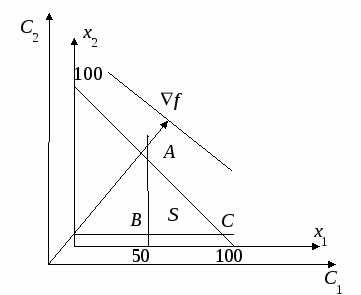целевой функции f показаны на рис. 5.3.


Рис 5.3

Решением данной задачи является точка A с координатами x₁=50, x₂=50, max f(x) = f(A) = 0,25·50+0,3·50 = 27,5 млн долларов.