УЧЕБНИК-Шеремет. Управленческий учет. Учебное пособие Под редакцией А. Д. Шеремета Подготовлено при финансовом содействии
 Скачать 5.06 Mb. Скачать 5.06 Mb.
|
РезюмеЛинейное программирование является наиболее популярным методом моделирования в принятии управленческих решений в случае, когда необходимо оптимизировать использование данного множества ограниченных ресурсов. Модель линейного программирования часто рассматривается как расширение моделей «затраты — объем — прибыль» и моделей распределения ресурсов в условиях многопродуктовых производств. Мы рассмотрели два метода нахождения оптимального решения — метод проб и ошибок и графический метод. Оба они позволяют понять, каким образом в модели линейного программирования выбирается оптимальное решение. Для использования этой модели на практике, когда есть большое количество продуктов и значительное число ограничений, следует применять методы, реализованные в стандартных компьютерных программах. Приложение 1. Хозяйственная ситуацияПрименение модели линейного программирования Компания «Металлик» открыла новый цех по производству двух продуктов: металлических поддонов и аккумулирующих устройств. Этот цех готов начать работу, имея в распоряжении 5 металлоформовочных и 5 металлорежущих станков, которые взяты в аренду у местной арендной фирмы за 30 ДЕ в месяц для каждого станка. Производственная мощность каждого станка составляет 400 часов в месяц. Дополнительные станки не могут быть получены. Количество машино-часов на производство единицы продукции: 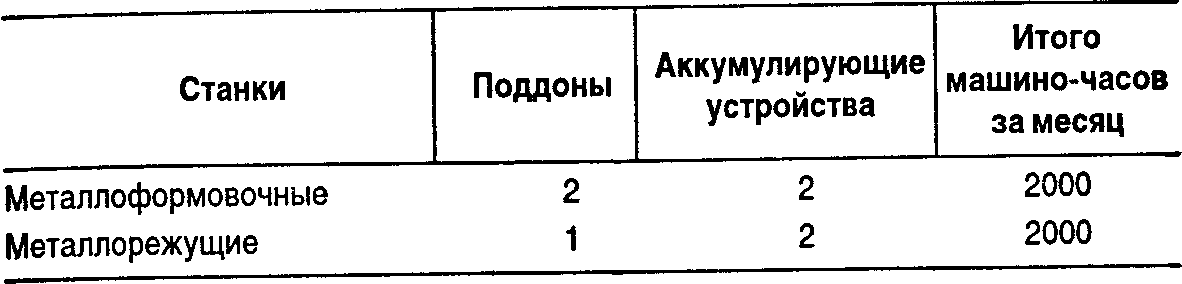 Бухгалтер цеха представил следующие данные: (ДЕ) 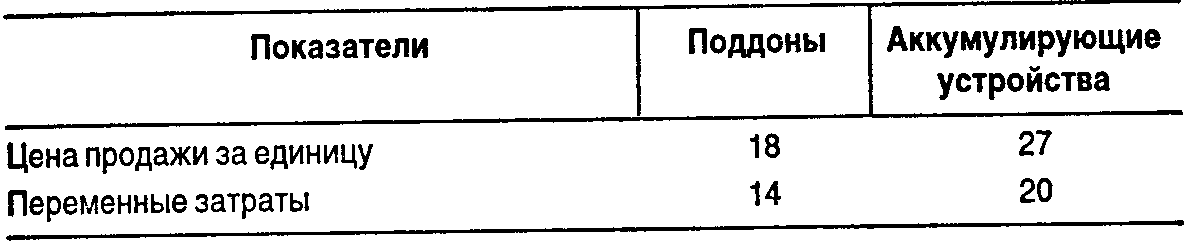 Спрос на аккумулирующие устройства неограничен, а относительно поддонов «Металлик" полагает, что их можно продать не более 800 шт. в месяц. Сформулирована модель линейного программирования, и соответствующий график иллюстрируют эту ситуацию. «Металлик» рассчитывает максимизировать суммарную маржинальную прибыль от новых операций, придерживаясь некоторых ограничений. Компания намеревается достичь оптимального уровня, который определен в точке, обозначенной на графике ОР. Модель линейного программирования Максимизировать СМП= 4 ДЕ • П + 7 ДЕ • У при условиях: П+2-У≤2000; 2 •П+2-У≤2000; ПС 800; П, У э О, где П— количество произведенных и проданных поддонов; У— количество произведенных и проданных аккумулирующих устройств; СМП— суммарная маржинальная прибыль. Графическое представление 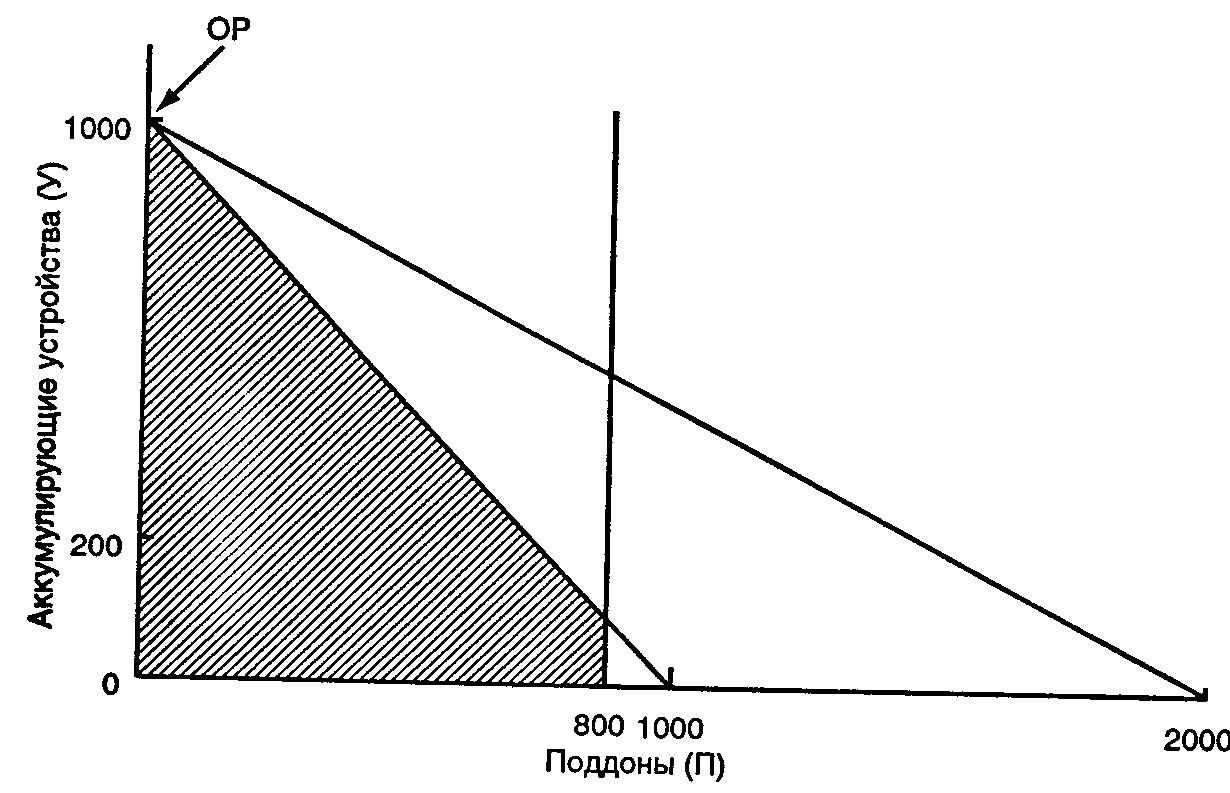 Каждую из следующих ситуаций рассмотрите независимо. А. Вычислите максимальную суммарную маржинальную прибыль, которая может быть получена, если цена продажи аккумулирующего устройства снизится с 27 до 23 ДЕ. Б. Определите максимальную сумму, которая может быть потрачена на рекламу для того, чтобы увеличить спрос на поддоны до 1000 шт. в месяц. В. Определите эффект влияния на операционную прибыль возврата одного металлоформовочного станка арендной фирмы, предполагая, что затраты на аренду устранимые. Приложение 2. Домашние упражненияЗадания 1. Оптимальный производственный план. Корпорация «IT» собирает и продает два продукта — принтеры и компьютеры. Покупатели могут купить отдельно компьютер либо компьютер вместе с принтером. Принтеры отдельно от компьютера не продаются. В результате количество проданных принтеров меньше или равно количеству проданных компьютеров. Маржинальная прибыль на один компьютер составляет 100 ДЕ, а на один принтер — 200 ДЕ. На сборку каждого принтера уходит 6 ч на производственной линии 1 и 10 ч на производственной линии 2, на сборку каждого компьютера—4 ч на производственной линии 1. (Многие узлы компьютера уже собраны внешними поставщиками.) Производственная линия 1 работает 24 часа в сутки, производственная линия 2—20 часов в сутки. Пусть х— количество принтеров, a y — количество компьютеров. А. Выразите все взаимосвязи в модели линейного программирования. Б. Какая комбинация принтеров и компьютеров будет максимизировать операционную прибыль корпорации «IT». Используйте для решения задачи графический метод и метод проб и ошибок. 2. Минимизация затрат, структура удобрений. Агротехнический центр, по совету Сэма Брауна, решил распылить по крайней мере 4800 фунтов специального азотного удобрения и по крайней мере 5000 фунтов специального фосфатного удобрения, чтобы увеличить свой урожай. Никакие другие ингредиенты в чистом виде не нужны. Дилер предлагает 100-фунтовые пакеты VIM по цене 10 ДЕ за каждый. Один пакет VIM содержит эквивалент 20 фунтов азота и 80 фунтов фосфата. Доступны также 100-фунтовые пакеты VOOM по цене 30 ДЕ за один пакет. Этот пакет содержит эквивалент 75 фунтов азота и 25 фунтов фосфата. Пусть х — количество пакетов VIM, ay— количество пакетов VOOM. Определите, сколько пакетов VIM и VOOM должен закупить агротехнический центр для того, чтобы получить необходимые удобрения при минимальных затратах. Решите проблему графически. 3. Оптимальный ассортимент продукции. Корпорация «Олвейс» располагает сетью продовольственных магазинов, открытых 24 часа в сутки. Каждый магазин имеет стандартную торговую площадь 40 000 футов2. Все товары классифицированы по двум группам: бакалейно-га-строномические и товары повседневного спроса. «Олвейс» требует, чтобы каждый магазин отводил минимум 10 000 футов2 под бакалейно-гастрономические товары и минимум 8 000 футов2 под товары повседневного спроса. В рамках этих ограничений управляющий магазина может выбирать ассортимент продукции. Управляющий магазина в городегоценивает маржинальную прибыль на 1 фут2 площади: бакалейно-гастрономические товары 10 ДЕ; товары повседневного спроса 4 ДЕ. А. Сформулируйте проблему, стоящую перед управляющим магазином, как модель линейного программирования. Буквой G обозначьте количества футов2 торговой площади для бакалейно-гастрономических товаров, а буквой D— футы2 площади для товаров повседневного спроса. Б. Почему «Олвейс» устанавливает минимальные границы на торговые площади для каждого вида товаров? В. Определите оптимальную структуру (ассортимент) двух видов товаров для магазина в городе Z. Используйте метод проб и ошибок и графический метод. В последнем случае на горизонтальной оси отметьте данные о бакалейно-гастрономических товарах, а на вертикальной оси — о товарах повседневного спроса. |
