УЧЕБНИК-Шеремет. Управленческий учет. Учебное пособие Под редакцией А. Д. Шеремета Подготовлено при финансовом содействии
 Скачать 5.06 Mb. Скачать 5.06 Mb.
|
16.2. Этапы решения проблемы линейного программированияПроблема линейного программирования решается в три этапа: 1. Определение цели. Целевая функция выражает определенную цель, которая должна быть максимизирована (например, операционная прибыль) или минимизирована (например, операционные затраты). 2. Определение основных взаимосвязей. Эти взаимосвязи включают ограничения, выраженные как линейные функции. Ограничение — это математическое неравенство (или равенство), которому должны удовлетворять все переменные в математической модели. 3. Нахождение оптимального решения. В случае, когда в целевой функции только две переменные и количество ограничений небольшое, для нахождения оптимального решения можно использовать графический метод и метод проб и ошибок. В более сложных случаях, которые возникают на практике, необходимы специальные пакеты программного обеспечения, например симплекс-метод. На данных нашего примера опишем три этапа решения проблемы ЛП. Напомним, что А — это количество произведенных моторов для снегоходов, а В — количество произведенных лодочных моторов. Этап 1. Определение цели. Главная цель — найти комбинацию продуктов, которая максимизирует суммарную маржинальную прибыль. Линейная функция, которая выражает эту цель, такая: суммарная маржинальная прибыль = 200 ДЕ • А + 250 ДЕ • В. Этап 2. Определение основных взаимосвязей. Взаимосвязи могут быть описаны неравенствами: ограничение по цеху 1 (сборка) 1.5 • А + 2,0 • В ≤ 300; ограничение по цеху 2 (контроль и испытание) 1,0 • А+0,5 • В ≤ 120; ограничение из-за недостатка материалов для изделия В В ≤ 126; Так как отрицательное производство невозможно, A ≥ 0 и В ≥ 0. На графике показаны три линии, характеризующие ограничения по цехам 1 и 2 и из-за недостатка материалов. Область возможных решений на графике показывает границы возможных комбинаций изделий, т.е. комбинации количеств моторов для снегоходов и лодочных моторов, которые удовлетворяют всем ограничивающим факторам. На графике эта область заштрихована. Линейное программирование — графическое решение 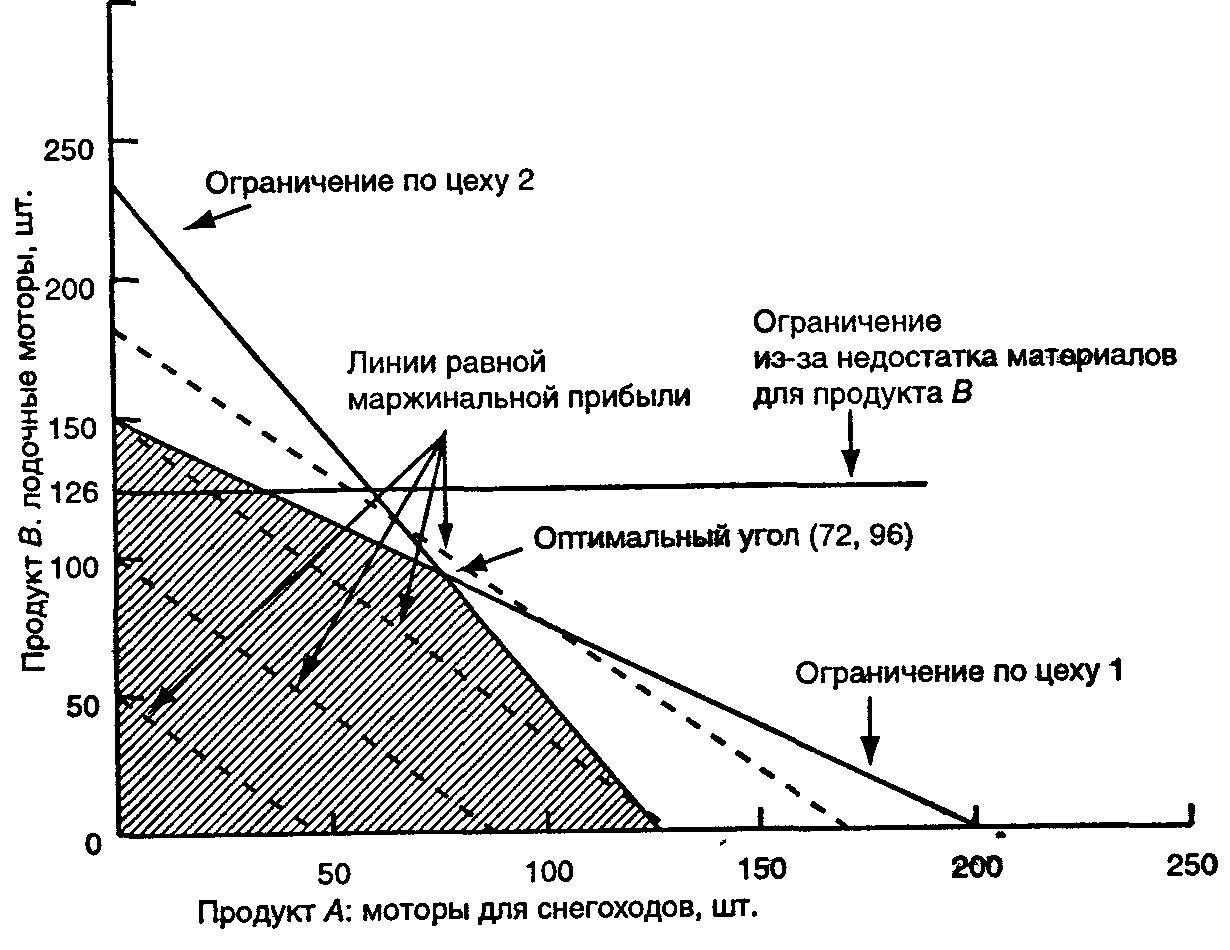 Этап 3. Нахождение оптимального решения. Для нахождения оптимального решения рассмотрим метод проб и ошибок, а затем графический метод. 16.3. Метод проб и ошибок и графический метод в определении оптимального решенияМЕТОД ПРОБ И ОШИБОК. Этот метод очень прост. Оптимальное решение может быть найдено в результате перебора координат углов области возможных решений. 1. Выбираем некоторую угловую точку и вычисляем суммарную маржинальную прибыль. Как видно на графике, область возможных решений имеет пять угловых точек. Полезно одновременно использовать уравнения для проверки координат. Например, точку (-4 =72, В = 96) найдем решением двух соответствующих неравенств как системы уравнений: 1,5 • А + 2,0 • В = 300 (ДЕ); (1) 1,0 • А + 0,5 • В = 120 (ДЕ). (2) Умножая уравнение (2) на 1,5, получим 1,5 • А + 0,75 • В = 180 (ДЕ). (3) Вычитая уравнение(3)из уравнения(1), имеем 1,25 • В = 120 (ДЕ); В = 120:1,25 = 96 (ДЕ). Подставляя значение В в уравнение (2), получим: 1,0 • А + 0,5 •96 = 120 (ДЕ); А = 120-48 = 72 (ДЕ). Зная значения А и В, можем рассчитать суммарную маржинальную прибыль (СМП): СМП = 200 ДЕ • 72 + 250 ДЕ • 96 = 34 400 ДЕ. 2. Двигаемся от одной угловой точки к другой и сравниваем СМП в данной точке с аналогичной величиной в каждой из ранее рассмотренных точек. Данные этих вычислений от угла к углу следующие: 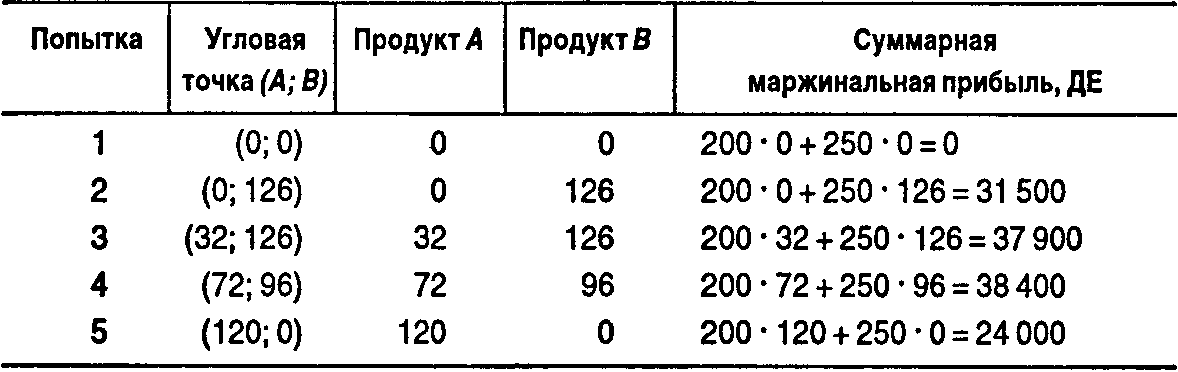 Оптимальная структура продукции составляет 72 мотора для снегоходов и 96 лодочных моторов. Следует отметить, что метод проб и ошибок, а также графический метод полезны в случае двух или, возможно, трех переменных. Для решения проблемы линейного программирования со многими переменными эти методы непрактичны. Стандартные программные пакеты для персональных компьютеров реализуют в этом случае симплекс-метод, который представляет собой итеративный пошаговый процесс. Он начинается выбором одного возможного решения с последующим замещением его, если результат можно улучшить. Этот перебор продолжается до тех пор, пока дальнейшее улучшение перестает быть возможным. Таким образом находят оптимальное решение. ГРАФИЧЕСКИЙ МЕТОД. Согласно данному методу оптимальное решение должно находиться в одной из уголовых точек области возможных решений. Почему? Изучим все возможные комбинации, которые дадут одинаковую маржинальную прибыль, равную, скажем, 10 000 ДЕ. Другими словами,имеем 200ДЕ •А = 250ДЕ • В = 10000 ДЕ. Это множество значений при маржинальной прибыли, равной 10 000 ДЕ, представлено прямой пунктирной линией через точки (А = 50; В = 0) и (А = 0; В = 40). Множества при других равных суммарных маржинальных прибылях могут быть представлены линиями, параллельными указанной линии. На графике мы видим три таких линии. Суммарная маржинальная прибыль увеличивается вместе с тем, как линии удаляются от первоначальной. Оптимальная линия есть самая дальняя от первоначальной линия, которая включает возможное решение. Эта точка есть угловая точка с координатами (А =72; В = 96). Вообще говоря, оптимальное решение для проблемы максимизации находится в угловой точке, где пунктирная линия пересекает крайнюю точку области возможных решений. Угол наклона целевой функции (пунктирной линии, представляющей равную СМП) может быть найден из уравнения СМП=200ДЕ•А+250ДЕ•В. Для нахождения угла наклона (величины изменения В в результате одной добавочной единицы А) это уравнение следует разделить на коэффициент при переменной В и затем перенести В в левую часть уравнения: СМП 200ДЕ 250 ДЕ = 250 ДЕ • А + В;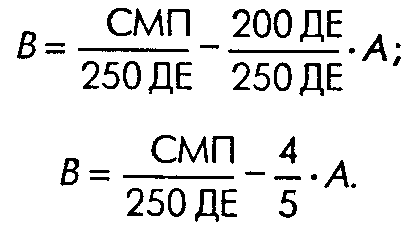 Угол наклона целевой функции отрицателен и равен 200 ДЕ/ 250 ДЕ, или 4/5. Графический подход обеспечивает очень простой и наглядный способ нахождения оптимального решения в модели ЛП, хотя его применение ограничено двумя продуктами в целевой функции (так как решение может быть представлено на двухмерном графике). |
