УЧЕБНИК-Шеремет. Управленческий учет. Учебное пособие Под редакцией А. Д. Шеремета Подготовлено при финансовом содействии
 Скачать 5.06 Mb. Скачать 5.06 Mb.
|
Приложение 2. Вопросы для самопроверки1. В решении о принятии специального заказа будущие постоянные затраты: а) являются нерелевантными; б) являются обычно релевантными; в) могут быть релевантными. 2. Фактические (исторические) затраты могут быть: а) релевантными при решении о будущем; б) полезными в прогнозировании будущих затрат; в) оба ответа верны; г) ни один из ответов не верен. 3. Компания по аренде автомобилей сравнивает две модели автомобилей, чтобы пополнить свой парк. Количественный фактор при принятии решения будет включать различия: а) в предполагаемом количестве миль на один галлон горючего; б) в комфорте и удовлетворении вкусов заказчиков; в) и в том, и в другом; г) ни в том, ни в другом. 4. Альтернативные затраты: а) обычно не включаются в бухгалтерские отчеты; б) не требуют денежных расходов; в) оба ответа верны; г) ни один из ответов не верен. 5. В принятии решения по замене оборудования могут быть релевантными: а) остаточная стоимость старого оборудования; б) ликвидационная стоимость старого оборудования; в) и та, и другая; г) ни та, ни другая. 6. Вообще говоря, все переменные затраты являются релевантными при принятии решений, а все постоянные затраты — нерелевантны: а) да; б) нет. 7. Специальный заказ, который может быть выполнен на имеющихся производственных мощностях, никогда не будет принят по цене продажи ниже полных затрат на единицу, включающих все постоянные и переменные затраты: а) да; б) нет. 8. Релевантные доходы — это ожидаемые будущие доходы, которые различаются при альтернативных вариантах при принятии управленческих решений: а) да; б) нет. 9. Когда многопродуктовый завод работает на полную мощность, заказы, которые принимаются, должны максимизировать: а) количество машино-часов; б) суммарную маржинальную прибыль; в) среднюю маржинальную прибыль на единицу ограниченного ресурса; г) количество трудовых затрат (человеко-часов); д) количество квадратных метров производственной площади. 10. Подход, который более полезен при решении принять специальный заказ или нет в ситуации, когда производственные мощности позволяют его выполнить: а) маржинальный подход; б) метод учета полных затрат. 11. Затраты, которые являются релевантными, могут включать: а) ожидаемые будущие постоянные затраты; б) прошлые переменные затраты; в) и те, и другие; г) ни те, ни другие. 16. МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В УПРАВЛЕНЧЕСКОМ УЧЕТЕОсновная проблема, которая решается при помощи линейного программирования,-.- оптимальное распределение ограниченных ресурсов для достижения поставленной цели, такой, как максимизация прибыли или минимизация потребляемых ресурсов. Все взаимозависимости между экономическими показателями в модели линейного программирования линейны. Данная модель широко применяется в таких отраслях, как очистка нефти, производство химических препаратов, обработка пищевых продуктов, где имеются многопродуктовые производства или многокомпонентные продукты. Бухгалтеры, которые могут понять входные и выходные данные, предположения и ограничения линейного программирования, играют огромную роль в управлении предприятием. Модель линейного программирования используется при решении таких управленческих задач, как определение ассортимента (номенклатуры) продукции, замещение и сочетание исходных материалов, производственное календарное планирование, наиболее часто встречающихся в краткосрочных моделях распределения ресурсов. В этой модели предполагается, что есть данный набор ресурсов и эти ресурсы обеспечивают определенный уровень реальных затрат. Основная цель руководителя заключается в выборе видов товаров и услуг, а также объемов, которые следует производить (продавать). 16.1. Предположения, лежащие в основе модели линейного программированияРанее была продемонстрирована важность фактора ограниченности ресурсов для принятия решения об ассортименте продукции. Наиболее выгодный (прибыльный) продукт — это не всегда продукт с наивысшей маржинальной прибылью на изделие. Наоборот, наиболее прибыльный продукт — это тот, который приносит наибольшую прибыль на единицу ограничивающего ресурса или ограничивающего фактора, например такого, как имеющиеся суммарные машино-часы. На практике обычно существует более чем одно ограничение. Следовательно, проблема заключается в максимизации суммарной маржинальной прибыли при данном множестве ограничений. Модель линейного программирования (ЛП) используется при решении проблем, где предположение о линейности является приемлемым. Применяя модель ЛП, мы предполагаем, что только один фактор — объем выпуска — вызывает изменение в суммарных затратах на продукцию. Все прочие затраты предполагаются фиксированными. Для многих краткосрочных решений это предположение достаточно приемлемо. Там, где это предположение неприемлемо, прибегают к другим моделям. Пример. Определение оптимального ассортимента продукции. Компания производит моторы. На ее заводе собирают и испытывают моторы двух видов — для снегоходов и для лодок (подвесной). Каждая модель проходит два подразделения — цех сборки и цех контроля и испытаний. Исходные данные:  Предположим, что цех работает с мотором одного вида. Из таблицы видно, что цех сборки может собирать максимум 200 моторов для снегоходов (300 машино-ч: 1,5 машино-ч/шт. = 200 шт.) или 150 шт. для лодок (300 маши-но-ч: 2,0 машино-ч /шт. = 150 шт.). Аналогично цех контроля и испытаний может протестировать 120 моторов для снегоходов (120 шт.: 1 ч = 120 шт.) или 240 лодочных моторов (120 шт.: 0,5 ч = 240 шт.). 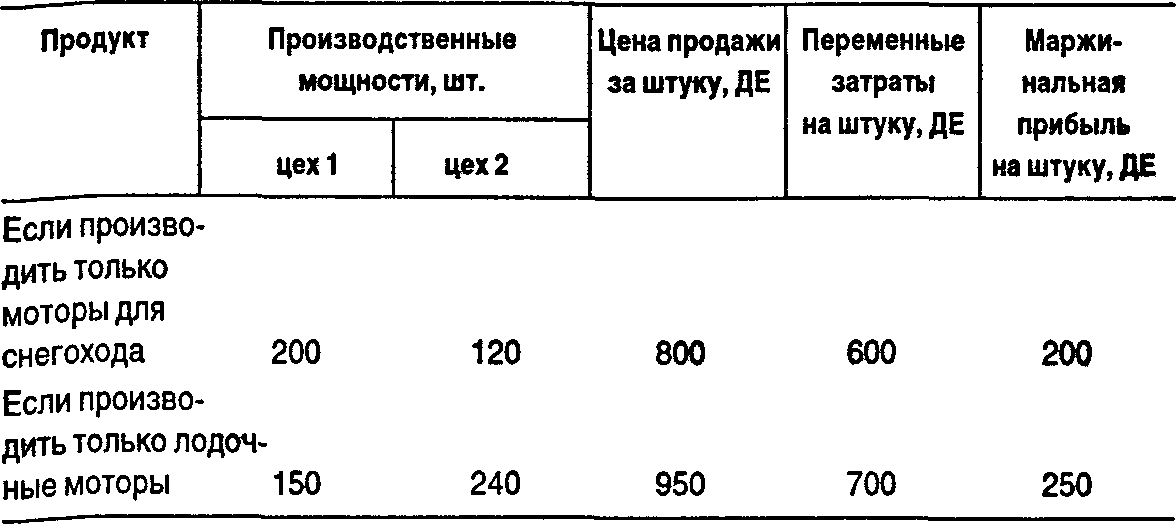 Обобщим эти и другие релевантные данные. Отметим, что по моторам для снегоходов маржинальная прибыль на штуку составляет 200 ДЕ, а по лодочным моторам — 250 ДЕ на один мотор. Известно также, что недостаток (некомплектность) исходных материалов для лодочных моторов будет ограничивать их производство до 126 моторов в день. Сколько моторов каждого вида должно быть произведено ежедневно, чтобы получить максимальную прибыль? |
