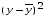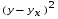методичка. Учебное пособие Рекомендовано учебнометодическим объединением умож д. в качестве учебного пособия для студентов экономических специальностей
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
|
Парная корреляция – это связь между двумя показателями, один из которых является факторным, а другой – результативным. Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем. Наиболее широкое применение в экономических исследованиях нашли приёмы корреляционного анализа, которые позволяют количественно выразить взаимосвязь между показателями. Условия применения корреляционного анализа 1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов). 2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации. Применение корреляционного анализа позволяет решить следующие задачи:
Исследование корреляционных соотношений имеет огромное значение в экономическом анализе. Это проявляется в том, что значительно углубляется факторный анализ, устанавливается место и роль каждого фактора в формировании уровня исследуемых показателей, углубляются знания об изучаемых явлениях, определяются закономерности их развития и, как итог, – точнее обосновываются планы и управленческие решения, более объективно оцениваются итоги деятельности предприятий и более полно определяются внутрихозяйственные резервы. 6.2. Использование способов парной корреляции для изучения стохастических зависимостей Одной из основных задач корреляционного анализа является определение влияния факторов на величину результативного показателя (в абсолютном измерении). Для решения этой задачи подбирается соответствующий тип математического уравнения, которое наилучшим образом отражает характер изучаемой связи (прямолинейной, криволинейной и т.д.). Это играет важную роль в корреляционном анализе, потому что от правильного выбора уравнения регрессии зависит ход решения задачи и результаты расчётов. Наиболее простым уравнением, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой YX = а + bx, (6.1) где x – факторный показатель; Y – результативный показатель; a и b – параметры уравнения регрессии, которые требуется определить. Данное уравнение описывает такую связь между двумя признаками, при которой с изменением факторного показателя на определённую величину наблюдается равномерное возрастание или убывание значений результативного показателя. В качестве примера для иллюстрации корреляционного анализа прямолинейной зависимости могут быть использованы сведения об изменении среднесуточной производительности грузового вагона в зависимости от средней статической нагрузки на вагон (табл. 6.1). Таблица 6.1 Исходные данные для определения тесноты связи между среднесуточной производительностью грузового вагона и средней статической нагрузкой
Определим среднеарифметические значения показателей Y и x по формулам (6.2) и (6.3): 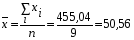 ; (6.2) ; (6.2) 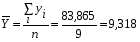 , (6.3) , (6.3)где n = 9, i = 1,….,9. Дальнейшим вычислениям придаётся табличная форма, что повышает их наглядность (табл. 6.2). Таблица 6.2 Расчёт производных величин для определения параметров уравнения связи и коэффициента корреляции
Теснота связи между показателями производительности вагона и средней статической нагрузкой измеряется коэффициентом корреляции, который исчисляется по формуле (6.4). 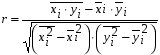 . (6.4) . (6.4)Подставляя необходимые значения в формулу (6.4), получаем 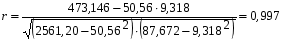 . .Коэффициент корреляции может принимать значения от 0 до 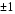 . Чем ближе его величина к 1, тем более тесная связь между изучаемыми явлениями, и наоборот. В данном случае величина коэффициента корреляции является весьма высокой (табл. 6.3). Это позволяет сделать вывод о том, что средняя статическая нагрузка на вагон является основным фактором, от которого зависит среднесуточная производительность грузового вагона. . Чем ближе его величина к 1, тем более тесная связь между изучаемыми явлениями, и наоборот. В данном случае величина коэффициента корреляции является весьма высокой (табл. 6.3). Это позволяет сделать вывод о том, что средняя статическая нагрузка на вагон является основным фактором, от которого зависит среднесуточная производительность грузового вагона.Таблица 6.3 Качественная оценка тесноты связи при различных значениях коэффициента корреляции и корреляционного отношения
Если коэффициент корреляции возвести в квадрат, получим коэффициент детерминации (d = 0,994). Он показывает, что производительность грузового вагона на 99,4 % зависит от средней статической нагрузки на вагон, а на долю других факторов приходится 0,6 % прироста производительности. Считая формулу связи линейной (y = a + bx), определим параметры a и b с помощью системы нормальных уравнений: 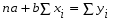 ; ; 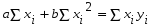 . .Значение 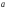 определяем из первого уравнения: определяем из первого уравнения:9a + 455,04b = 83,865; 455,04a + 23050,82b = 4258,32; 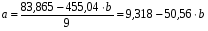 Подставляя найденное значение 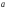 во второе уравнение, находим значение b: во второе уравнение, находим значение b: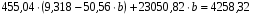 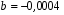 ; ;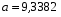 . .Итак, уравнение регрессии в окончательном виде получило следующий вид: 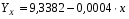 . .В случае, если с помощью корреляционного анализа линейная связь между показателями не обнаружена, определяется возможность криволинейной зависимости:
Если при увеличении одного показателя значения другого возрастают до определённого уровня, а потом начинают снижаться, то для записи такой зависимости лучше всего подходит парабола второго порядка (формула 6.5). В соответствии с требованиями метода наименьших квадратов для определения параметров 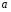 , , 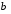 , и , и 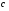 необходимо решить следующую систему уравнений: необходимо решить следующую систему уравнений: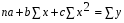 ; ;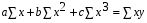 ; ;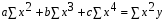 . .При более сложном характере зависимости между изучаемыми явлениями используются более сложные параболы (третьего, четвёртого порядка и т.д.), а также квадратические, степенные, показательные и другие функции. Гипербола описывает такую зависимость между двумя показателями, когда при увеличении одной переменной значения другой увеличиваются до определённого уровня, а потом прирост снижается. Для определения параметров гиперболы (формула 6.6) необходимо решить следующую систему уравнений 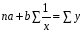 ; ;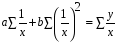 . .Теснота связи при криволинейной форме зависимости характеризуется корреляционным отношением 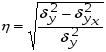 , (6.7) , (6.7) где 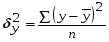 ; ; 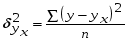 . .Показатель (6.7) является универсальным. Его можно применять при любой форме зависимости. Однако для определения его величины вначале необходимо решить уравнение регрессии и рассчитать выравненные значения результативного показателя (Yx), для чего в полученное уравнение необходимо подставить значения x (при гиперболической зависимости) и x, x2 (при параболической зависимости). В качестве примера для иллюстрации корреляционного анализа криволинейной зависимости могут быть использованы сведения об изменении величины эксплуатационных расходов в зависимости от грузооборота (табл. 6.4). Таблица 6.4 Зависимость эксплуатационных расходов (y) от грузооборота (x)
Подставив полученные значения в систему уравнений для определения параметров гиперболы, получим: 9a + 0,0773b = 2632,25 0,0773a + 0,00072b = 24,865 Значение 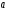 определяем из первого уравнения: определяем из первого уравнения: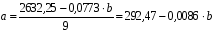 . .Подставляя найденное выражение 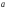 во второе уравнение, находим значение b: во второе уравнение, находим значение b: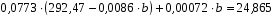 ; ;b = 37616,7; a = - 31,03. Уравнение гиперболы будет иметь следующий вид: 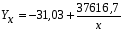 . .Параметры полученного уравнения экономического смысла не имеют. Если подставить в данное уравнение соответствующие значения x, то получим выравненные значения эксплуатационных расходов в зависимости от грузооборота. Результаты приведены в последней графе табл. 6.4. Для расчёта корреляционного отношения (формула 6.7), характеризующего тесноту связи при криволинейной зависимости, заполним табл. 6.5. Таблица 6.5 Расчёт исходных данных для определения корреляционного отношения при криволинейных зависимостях
Определим среднеарифметическое значение показателя y: 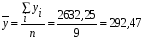 . .Подставив полученные значения в формулу (6.7), определим величину корреляционного отношения: 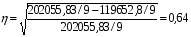 . .В данном случае величина корреляционного отношения является заметной (табл. 6.3). Это позволяет сделать вывод о том, что грузооборот – один из основных факторов, от которого зависит величина эксплуатационных расходов железной дороги. В заключение необходимо отметить, что мы рассмотрели использование способов парной корреляции только на двух примерах. Однако эта методика может быть использована для исследования соотношений между разными экономическими показателями, что позволяет значительно углубить знания об изучаемых явлениях, определить место и роль каждого фактора в изменении уровня исследуемого показателя. 6.3. Методика множественного корреляционного анализа Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества факторов. Как правило, каждый фактор в отдельности не определяет изучаемое явление во всей полноте. Только комплекс факторов в их взаимосвязи может дать более или менее полное представление о характере изучаемого явления. Корреляционно-регрессионный анализ включает следующие этапы:
Отбор факторов для корреляционного анализа является очень важным моментом. От того, насколько правильно он сделан, зависит точность выводов по итогам анализа. При этом необходимо придерживаться следующих правил.
Исходя из перечисленных выше требований, для многофакторной корреляционной модели уровня среднесуточной производительности локомотива в грузовом движении (Y) возьмём следующие факторы: X1 – средний вес поезда, тонны; X2 – среднесуточный пробег локомотива в грузовом движении, км; X3 – средняя статическая нагрузка на вагон, тонны; X4 – грузооборот, млн. тариф. т-км; X5 – средняя участковая скорость движения грузовых поездов, км/ч; X6 – полное время оборота вагона, сутки. Исходная информация представлена в табл. 6.6. Таблица 6.6 Исходные данные для корреляционного анализа
Рассчитаем матрицу парных коэффициентов корреляции (табл. 6.7). Таблица 6.7 Матрица парных коэффициентов корреляции
Коэффициенты парной корреляции характеризуют тесноту связи между двумя показателями в общем виде с учётом взаимосвязей факторов, оказывающих воздействие на результативный показатель. Данные табл. 6.7 (первый столбец) свидетельствуют об ощутимом воздействии на уровень среднесуточной производительности локомотива таких факторов, как средний вес поезда, среднесуточный пробег локомотива в грузовом движении и средняя статическая нагрузка на вагон. Так как коэффициенты парной корреляции у данных показателей имеют существенную величину, то их можно выбрать для построения многофакторной корреляционной модели. Чаще всего на практике применяется линейное уравнение множественной регрессии y = a0 + a1x1 + a2x2 +…+ anxn, (6.8) где y – результативный показатель; x1, x2,… xn – факторы; ai – параметры уравнения. Для определения коэффициентов регрессионного уравнения (6.8) удобнее всего использовать методы матричного исчисления. Для этого сделаем одно допущение, которое не меняет условия задачи. Будем считать, что в уравнении (6.8) свободный член a0 всегда умножается на некоторый фиктивный фактор, имеющий постоянное значение, равное единице, т.е. имеем y = a0x0 + a1x1 + a2x2 +…+ anxn. В исходной статистической матрице (6.9), составленной по данным табл. 6.6, появляется ещё один столбец, все значения которого равны единице. 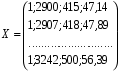 . (6.9) . (6.9)Введём также вектор результативного показателя (6.10): 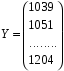 . (6.10) . (6.10)Для расчёта параметров уравнения регрессии воспользуемся формулой (6.11): 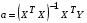 (6.11) (6.11)В нашем примере параметры уравнения регрессии равны: a0 = -351,057; a1 = 0,512; a2 = 1,787; a3 = -17,658. Таким образом, уравнение зависимости производительности локомотива от среднего веса поезда, среднесуточного пробега локомотива и статической нагрузки на вагон будет иметь следующий вид: y = -351,057 + 0,512x1 + 1,787x2 – 17,658x3. (6.12) На следующем этапе анализа необходимо убедиться в значимости полученной модели. Выдвигаем нулевую гипотезу Н0: а1=а2=…=аm=0 (регрессии нет). Конкурирующая гипотеза – хотя бы один коэффициент регрессии отличен от нуля. Методика проверки разработана Фишером. В её основе лежит дисперсионный анализ. В качестве меры факторного влияния используется величина 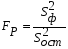 , (6.13) , (6.13)где 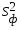 - факторная дисперсия, характеризующая изменчивость результативного показателя под действием факторов; - факторная дисперсия, характеризующая изменчивость результативного показателя под действием факторов; 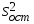 - остаточная дисперсия, применяемая здесь в качестве оценки дисперсии случайной составляющей. - остаточная дисперсия, применяемая здесь в качестве оценки дисперсии случайной составляющей.Факторная дисперсия определяется по формуле (6.14): 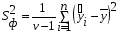 . (6.14) . (6.14)Остаточная дисперсия определяется по формуле (6.15): 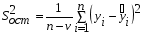 , (6.15) , (6.15)где v – число оцениваемых параметров, учитывая свободный член уравнения; 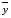 - среднее арифметическое значение результативного показателя; - среднее арифметическое значение результативного показателя; 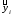 - расчётное значение y, соответствующее i-му наблюдению, n – количество наблюдений. - расчётное значение y, соответствующее i-му наблюдению, n – количество наблюдений.В нашем примере 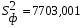 ; ; 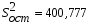 . . Таким образом, 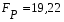 . .Фактическая величина F-отношения сопоставляется с табличной и делается заключение о надёжности связи. F-теоретическое рассчитывается по таблице значений F с k1 = (v – 1) и k2 = (n – v) степенями свободы. При уровне вероятности p = 0,05 и количестве степеней свободы k1=3 и k2=5 F-теоретическое составляет 5,41. Поскольку FР>FТАБ, то гипотеза об отсутствии регрессии отклоняется. Это свидетельствует о значительной тесноте связи между изучаемыми показателями. Для статистической оценки точности уравнения регрессии рассчитывается также средняя ошибка аппроксимации: 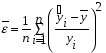 . (6.16) . (6.16)Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической, тем меньше средняя ошибка аппроксимации. В нашем примере она составляет 1,038 %. Учитывая, что в экономических расчётах допускается погрешность 5-8 %, можно сделать вывод, что исследуемое уравнение регрессии довольно точно описывает изучаемые зависимости. А значит, его можно использовать для практических целей. Вопросы для обсуждения 1. Перечислите условия применения корреляционного метода. 2. Что показывает уравнение регрессии? 3. В какой последовательности применяется корреляционно-регрессионный метод изучения линейной и нелинейной форм связи? 4. Каковы условия отбора факторов для корреляционного анализа? 5. На основе расчёта каких показателей даётся статистическая оценка результатов корреляционного анализа? 7. Системный подход к экономическому анализу и поиск резервов повышения эффективности производства (перевозок, работ, услуг) 7.1. Сущность системного подхода к изучению хозяйственной деятельности филиалов ОАО «РЖД» Системный анализ – это совокупность научных методов и приёмов решения разнообразных проблем, возникающих в процессе деятельности общества. Выделяют несколько этапов проведения системного анализа. На первом этапе объект исследования представляется как система, для которой определяют цели и условия функционирования. Хозяйственную деятельность предприятия можно рассматривать как систему, состоящую из трёх взаимосвязанных элементов: ресурсов, производственного процесса и готовой продукции. Входом этой системы являются материально-вещественные потоки ресурсов (средств и предметов труда) и потоки трудовых ресурсов. Выходом – материально-вещественные потоки готовой продукции (перевозки, работы, услуги). Производственный процесс переводит вход системы в её выход, т.е. в результате производственного процесса производственные ресурсы, соединяясь, становятся готовой продукцией. Целью работы любого предприятия, в том числе и транспортного, является рентабельность, т.е. по возможности высокий результат в денежном выражении за рассматриваемый период времени. Задача системного анализа – рассмотреть все частные факторы, обеспечивающие более высокий уровень рентабельности. Экономический принцип деятельности предприятия – обеспечение либо максимального выпуска продукции (работ, услуг) при данных затратах ресурсов, либо альтернативно заданного выпуска продукции (работ, услуг) при минимальном расходе ресурсов. Условия функционирования транспортного предприятия определяются системой долговременных экономических нормативов налогообложения и внешнеэкономическими связями предприятия, т.е. рынком финансирования, рынком купли и рынком продажи. Для проведения системного экономического анализа необходима разработка качественных характеристик экономики предприятия – системы синтетических и аналитических показателей. Отбор показателей, характеризующих финансово-хозяйственную деятельность предприятия, осуществляется на втором этапеанализа. На третьем этапе проведения системного экономического анализа составляется общая схема системы, устанавливаются её главные компоненты, функции, взаимосвязи, разрабатывается схема подсистем, показывающая соподчинение их элементов. На основе информационной модели хозяйственной деятельности, т.е. модели формирования экономических факторов и показателей, составляется общая блок–схема комплексного экономического анализа, классифицируются факторы и показатели, формализуются связи между ними (рис. 7.1). 3. Анализ использования основных фондов и оборудования 4. Анализ использования материальных ресурсов 5. Анализ показателей использования трудовых ресурсов 6. Анализ объёма, структуры и качества транспортной продукции (работ, услуг) 8. Анализ величины и структуры авансированных фондов 7. Анализ себестоимости перевозок (работ, услуг) 9. Анализ оборачиваемости производственных фондов 10. Анализ прибыли и рентабельности транспортной продукции 11. Анализ финансового состояния и платёжеспособности 12. Анализ рентабельности хозяйственной деятельности 13. Анализ экономического потенциала и деловой активности 2. Анализ показателей организационно-технического уровня, внешних условий и стадий жизненного цикла системы 1. Предварительный обзор обобщающих показателей Рис. 7.1. Общая блок – схема взаимосвязи показателей деятельности предприятия для комплексного анализа Связь между различными сторонами производственно-хозяйственной деятельности отражается на схеме в определённой соподчинённости различных показателей. В основе всех экономических показателей лежит предварительный обзор обобщающих показателей, который предполагает характеристику наличия необходимых материальных и финансовых ресурсов для нормального функционирования транспортного предприятия и выполнения его производственной программы. Затем проводится анализ организационно-технического уровня, т.е. производственной структуры предприятия, структуры управления, уровня концентрации и специализации производства, продолжительности производственного цикла, технической и энергетической вооружённости труда, степени механизации и автоматизации. Параллельно с организационно-техническим уровнем даётся оценка маркетинговой деятельности предприятия по изучению спроса на продукцию транспорта, её конкурентоспособности, конъюнктуры рынка, рекламы и т.д. Показатели блока 1 и блока 2 оказывают влияние на все остальные показатели хозяйствования и в первую очередь на объём производства транспортной продукции, её качество, на степень использования производственных ресурсов (производительность труда, фондоотдачу, материалоотдачу), а также на другие показатели экономической эффективности: себестоимость, прибыль, рентабельность и т.д. Эффективность использования производственных ресурсов проявляется в трёх направлениях:
Сопоставление показателей объёма и себестоимости перевозок характеризует величину прибыли и рентабельности транспортной продукции. Анализ показателей объёма транспортной продукции, работ, услуг и величины авансированных основных производственных фондов и оборотных средств характеризует воспроизводство и оборачиваемость производственных фондов (фондоотдача, оборачиваемость оборотных средств). Полученные показатели, в свою очередь, в сопоставимости определяют уровень рентабельности хозяйственной деятельности филиалов ОАО «РЖД». От выполнения плана по прибыли и в целом финансового плана, с одной стороны, и от оборачиваемости оборотных средств – с другой, зависит финансовое состояние и платёжеспособность железной дороги. Обобщающие показатели каждого блока называются синтетическими (интегральными). Например, объём реализованной транспортной продукции – синтетический показатель для блока 6, полная себестоимость этой продукции – для блока 7. Посредством этих обобщающих показателей осуществляется связь между отдельными блоками в системе экономического анализа. Каждый блок как относительно обособленная система формируется в систему аналитических показателей, из которых складываются эти синтетические показатели. Основными показателями блока 3 являются фондоотдача, фондоёмкость, среднегодовая стоимость основных средств производства, амортизация, капитальные вложения, ввод в действие основных производственных фондов, внедрение новой техники. В блоке 4 основными показателями являются материалоёмость, материалоотдача, стоимость использованных предметов труда за анализируемый отрезок времени. |

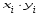
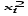
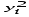
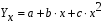 ; (6.5)
; (6.5)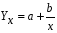 . (6.6)
. (6.6)