методичка. Учебное пособие Рекомендовано учебнометодическим объединением умож д. в качестве учебного пособия для студентов экономических специальностей
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
|
Метод суммирования всех показателей Комплексная оценка Ri каждого предприятия (года) определяется по формуле (5.1): 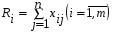 , (5.1) , (5.1)где j = 1, …n – количество показателей, i = 1, …m – количество предприятий (года в динамике). Данным методом пользуются в случае одинаковой направленности исходных показателей и их общей сопоставимости. Наилучшее предприятие (год) определяется по максимальной сумме показателей–стимуляторов и по минимальной сумме показателей-дестимуляторов. Таким образом, критерий оценки наилучшего предприятия (года) для показателей-стимуляторов – max 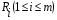 , а для показателей-дестимуляторов – min , а для показателей-дестимуляторов – min 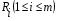 . .Метод суммы баллов При построении балльных оценок кроме исходных данных о значениях показателей задаются шкалы для оценки каждого показателя. Наиболее распространёнными являются непрерывные и дискретные шкалы. Они характеризуются минимальным и максимальным количеством баллов, которыми может быть оценён показатель. Верхняя и нижняя границы шкалы могут иметь как положительное, так и отрицательное значение, т.е. оценки могут быть и положительными, и отрицательными. Так, показатели выполнения плана по объёму перевозок, себестоимости могут оцениваться положительной и отрицательной величинами, а, например, показатели травматизма – только отрицательными величинами. Дискретная шкала задает определённое число уровней оценок (баллов), с помощью которых оценивается показатель. Как правило, в этом случае выбирается целочисленные балльные оценки. Например, показатель производительности труда может оцениваться одним из шести чисел: 0, 1, 2, 3, 4, 5, а качество перевозок – одним из трёх чисел: 0, 1, 2. В случае непрерывной шкалы оценки могут принадлежать любой точке некоторого отрезка, который определяет шкалу данного показателя. Например, показатель выполнения плана перевозок может оцениваться десятибалльной непрерывной шкалой, т.е. оценки выбираются из отрезка [0,10] и могут быть любыми числами, принадлежащими этому отрезку. Существуют следующие способы исчисления балльной оценки для конкретного значения показателя: непрерывное отображение отрезка, в пределах которого изменяется данный показатель на заданную шкалу; с помощью задания интервалов изменения показателя и соответствующих балльных оценок. Предположим, что известны значения показателей (матрица X), шкалы оценок по каждому показателю и способы оценки. Тогда можно построить вспомогательную матрицу B, где элементы матрицы – балльные оценки соответствующих показателей. Оценка Ri каждого предприятия (года) вычисляется по формуле (5.2): 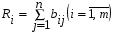 . (5.2) . (5.2) Критерий оценки наилучшего предприятия (года) - max 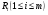 . .Метод суммы мест По исходным данным (по матрице X) строится вспомогательная матрица P по следующим правилам:
Оценка Ri каждого предприятия (подразделения, года и т.д.) вычисляется по формуле (5.3): 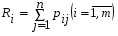 , (5.3) , (5.3)где j = 1, …n – количество показателей, i = 1, …m – количество предприятий (года в динамике). Критерий оценки наилучшего предприятия (года) - min 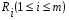 . .Этот метод, как и метод суммы баллов, не учитывает абсолютные значения показателей, и поэтому оценки могут существенно исказить картину достижений каждого предприятия. Метод расстояний В данном методе требуется определить по имеющейся информации предприятие–эталон (год-эталон). Это несуществующее реально предприятие (год), характеризующееся наилучшими значениями по каждому показателю среди всех имеющихся. Если столбец содержит показатель–стимулятор, то выбирается его максимальное значение, а если показатель является дестимулятором – выбирают минимальное его значение. Все найденные значения показателей образуют дополнительную строку (x01, x02, …x0n). Комплексная оценка Ri определяется по формуле (5.4): 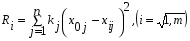 , (5.4) , (5.4)где j = 1, …n – количество показателей, i = 1, …m – количество предприятий (года в динамике); kj – коэффициент сравнительной значимости, необходимый для придания веса различным показателям в соответствии с их важностью. Чем больше kj, тем более значим показатель j, тем в большей степени отклонение от эталона будет влиять на общую суммарную оценку Ri. В нашем случае k1 = k2 =…= kn = 1. Критерий оценки наилучшего предприятия (года) - min 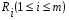 . . Метод расстояний наиболее формализованный из рассмотренных выше. Он легко позволяет учитывать значимость показателей, и его идея определения оценок как расстояний между точками–подразделениями и точкой–эталоном весьма убедительна. Вместе с тем и этот метод имеет ряд недостатков: процедура вычисления сложна, а результаты не столь наглядны. Таксонометрический метод Данный метод является обобщением метода расстояний. Так как все показатели имеют разную природу и несравнимые друг с другом значения, то необходимо нормировать данные показатели. Для этого проводят замену исходной матрицы X на матрицу Z, где каждый элемент zij рассчитывается по формуле (5.5): 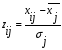 , (5.5) , (5.5)где 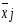 - среднее арифметическое всех уровней показателя j (столбца матрицы X); - среднее арифметическое всех уровней показателя j (столбца матрицы X);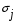 - среднеквадратичное отклонение показателя j. - среднеквадратичное отклонение показателя j.Их определяют следующим образом: 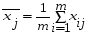 , (5.6) , (5.6)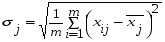 . (5.7) . (5.7)На следующем этапе производится формирование «эталонного» предприятия (года). Для этого в каждом столбце выбирается наибольшее (если показатель - стимулятор) или наименьшее (если показатель - дестимулятор) значение. Характеристика эталонного предприятия (года) – это дополнительная строка (z01, z02, …z0n). Комплексная оценка Ri определяется по формуле (5.8): 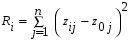 , (5.8) , (5.8)где j = 1, …n – количество показателей, i = 1, …m – количество предприятий (года в динамике). Критерий оценки - min 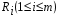 . .Таксонометрический метод оценки не только учитывает абсолютные значения показателей, но и позволяет элиминировать их различную вариацию. Пример: рассмотрим систему комплексной оценки деятельности железной дороги в динамике лет следующими методами: суммы мест, расстояний и таксонометрическим (табл. 5.1). Таблица 5.1 Исходные данные для сравнительной комплексной оценки деятельности железной дороги
Строка № 4 дана для характеристики показателей:
Алгоритм расчёта методом суммы мест
Расчёт комплексной оценки деятельности железной дороги в динамике лет методом суммы мест приведён в дополнительной табл. 5.2. Таблица 5.2 Расчёт сравнительной комплексной оценки методом суммы мест
Алгоритм расчёта методом расстояний
Таблица 5.3 Результаты расчёта сравнительной комплексной оценки методом расстояний
Например, комплексная оценка за 2001 г. рассчитывается следующим образом: 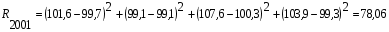 и т.д. Алгоритм расчёта таксонометрическим методом
Таблица 5.4 Исходные данные для сравнительной комплексной оценки деятельности железной дороги таксонометрическим методом
Пример расчёта значений показателей в табл. 5.4: Значение показателя объёма перевозок в 2001 г. определяется по формуле (5.5) и составляет 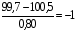 ; значение показателя объёма перевозок в 2002 г. составляет ; значение показателя объёма перевозок в 2002 г. составляет 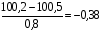 и т.д. и т.д.Значение показателя объёма эксплуатационных расходов в 2001 г. составляет 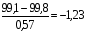 и т.д. и т.д.При этом среднее значение ( 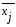 ) по показателю объёма перевозок рассчитывается по формуле (5.6) и составляет ) по показателю объёма перевозок рассчитывается по формуле (5.6) и составляет 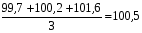 ; среднее значение по показателю объёма эксплуатационных расходов составляет ; среднее значение по показателю объёма эксплуатационных расходов составляет 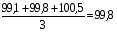 и т.д. и т.д.Среднеквадратичное отклонение ( 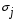 ) по показателю объёма перевозок определяется по формуле (5.7) и составляет: ) по показателю объёма перевозок определяется по формуле (5.7) и составляет: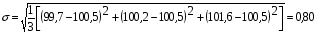 и т.д. и т.д.Результаты сравнительной комплексной оценки таксонометрическим методом представлены в табл. 5.5. Таблица 5.5 Результаты расчёта сравнительной комплексной оценки таксонометрическим методом
Например, комплексная оценка за 2001 г. рассчитывается следующим образом: 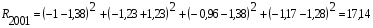 и т.д. и т.д.Сводка результатов расчётов по трём методам приведена в табл. 5.6. Таблица 5.6 Сводка результатов сравнительной комплексной оценки
Данные табл. 5.6 показывают, что по всем вариантам расчёта наилучшие результаты достигнуты железной дорогой в 2003 г., на втором месте находится 2002 г., на третьем – 2001 г., то есть в данном случае распределение лет, занявших первое и последнее места, одинаково независимо от метода расчёта и системы показателей. Это свидетельствует об «индивидуализированных» результатах деятельности железной дороги. Вопросы для обсуждения 1. Чем объясняется необходимость сравнительной комплексной оценки деятельности предприятия? 2. Приведите алгоритмы многомерных сравнений для комплексной оценки хозяйственной деятельности. 3. Каковы условия применения коэффициентов сравнительной значимости в ходе комплексной оценки результатов хозяйственной деятельности? 6. Способы изучения корреляционных (стохастических) взаимосвязей показателей работы железнодорожного транспорта 6.1. Понятие стохастической связи и задачи корреляционного анализа Стохастические зависимости чаще встречаются в экономических исследованиях, чем функциональные. Они отличаются приблизительностью, неопределённостью, проявляются только в среднем и по значительному количеству наблюдений (объектов). При стохастической зависимости каждой величине факторного показателя (аргумента) может соответствовать несколько значений результативного показателя (функции). Отличают парную и множественную корреляцию. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||