Развитие математической логики в 1930-х привело к усилению позиций конвенционали́зма. С формально-логической точки зрения для мира объектов возможны отличные системы классификаций. Так, согласно «принципу терпимости» Карнапа, в основе данной научной теории может находиться любой «языковой каркас», то есть любая совокупность правил синтаксиса. «Языковые формы» следует использовать с учетом их полезности. Это вполне просматривается в ИТ. Прагматизм примыкает к общей традиции конвенционали́зма. Соглашение, например, может быть проинтерпретировано через прагматическое понятие «уверенности». Также и Витгенштейн утверждал, что математика невозможна без «веры» в то, что все её предложения и формулы получаются или доказываются именно таким-то образом. Это активно используется в ИТ (немонотонные логики). Инструментализм (Джон Дьюи) рассматривает научные понятия, теории и гипотезы как инструменты, необходимые для ориентации человека в его взаимодействии с природой и обществом. Например, этническая идентичность, считают инструменталисты, — это не объективно существующая характеристика человека как члена какого-то этноса, а ситуативная роль, сознательный выбор, который делает человек или группа лиц для достижения политической власти или целей экономического характера. 4. Интуиционизм (Л. Э. Я. Брауэр, 1907) по-другому решает проблему парадокса Рассела. Это система философских и математических идей и методов, которая отвергает теоретико-множественный подход к определению математических понятий, а также некоторые способы рассуждения, принятые в классической логике. А именно, основным критерием истинности математического суждения является интуитивная убедительность возможности проведения мысленного эксперимента, связываемого с этим суждением. Что именно в классической математике критикуется? Естественно представить, что произвольное натуральное число может быть построено в виде последовательного ряда однородных предметов, например, ряда точек. Столь же естественно представить, что, построив некоторое натуральное число, можно построить затем и следующее, добавив к уже построенному ещё одну точку. Поэтому природа натуральных чисел является интуитивно ясной. Однако с «множеством всех натуральных чисел» не связывается никакого способа их мысленного построения, и его существование представляется сомнительным. Одним из источников возникновения такого рода «монстров» в классической математике являются теоремы чистого существования, в которых наличие искомого объекта утверждается лишь на основе формального опровержения гипотезы о его невозможности. Иначе говоря, фундамент таких теорем составляет представление об абсолютной непогрешимости законов классической логики. Это представление также стало одной из мишеней критики Брауэра. С его точки зрения, законы классической логики возникли в результате рассмотрения конечных совокупностей, при работе с которыми доказательство чистого существования заведомо может быть дополнено эффективным способом построения искомого объекта — полным перебором. При переходе же к рассмотрению бесконечных совокупностей эти законы становятся недостоверными, поскольку полного перебора таких совокупностей мы провести уже не можем. Появление антиномий (типа парадоксов Рассела) можно рассматривать как дополнительный довод в пользу неудовлетворительности теоретико-множественного подхода, но критика относится и к таким разделам математики, где антиномий не возникает. В чем отличие интуиционистской логики от классической? Любое суждение считается осмысленным, только если оно выражает возможность некоторого умственного построения, и считается истинным, только если исследователю удалось выполнить соответствующее построение. Примеры: утверждение, начинающееся с квантора существования, означает наличие способа мысленного построения искомого объекта. дизъюнкция 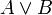 суждений A и B означает возможность непосредственно указать среди этих суждений верное. С этой точки зрения, суждение вида  может и не быть истинным, если проблема A не решена к настоящему времени. Отсюда видно, что закон исключённого третьего неприемлем в интуиционистской математике в качестве логического принципа. Соотношение теоретико-множественной (ТММ) и интуиционистской математик (ИМ) с точки зрения допускаемых логических средств и абстракций может быть охарактеризовано следующей таблицей: Теоремы и принципы | ТММ | ИМ | Закон исключенного третьего | Да | Нет | Закон двойного отрицания | Да | Нет | Принцип Маркова | Да | Нет | Абстракция актуальной бесконечности | Да | Частично | Тезис Черча | Да | Нет | |
Скачать 1.76 Mb.