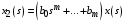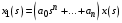Учебное пособие санктпетербург 2016 удк 681. 5 (075. 8) Ббк 22. 161я73 к 59 Рецензенты
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
2.1.3.2. Переходные характеристики Переходной характеристикой (ПХ) непрерывной системы или ее элемента называется реакция системы или элемента на ступенчатый сигнал, описываемый единичной ступенчатой функцией при нулевых начальных условиях (рис. 2.1) 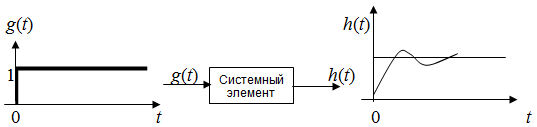 Рис. 2.1. Переходная характеристика на единичное входное воздействие Переходная характеристика может быть получена экспериментальным путем или аналитическим способом 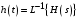 , ,где 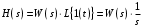 , , 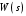 – передаточная функция системы или элемента. – передаточная функция системы или элемента. Таким образом, 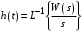 . .Весовой или импульсной переходной функцией w(t) называют функцию, описывающую реакцию динамического звена (системы) на идеальное импульсное воздействие δ(t) при нулевых начальных условиях (рис. 2.2). 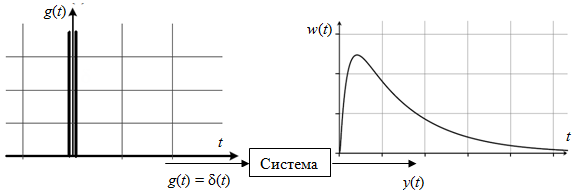 Рис. 2.2. Весовая переходная функция Математически идеальное импульсное воздействие описывается дельта-функцией δ(t): 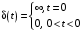 ; ; 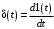 ; ; 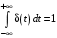 . .2.1.4. Частотные характеристики Существует два пути получения частотных характеристик: 1) экспериментально-физический, 2) теоретический. Первый путь состоит в том, что на систему подается синусоидальный сигнал постоянной амплитуды и переменной частоты (рис. 2.3). На выходе системы в установившемся режиме будет иметь место также синусоидальный сигнал той же частоты, но другой амплитуды и с фазовым сдвигом по отношению к входному сигналу. 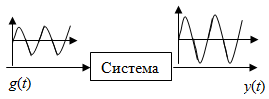 Рис. 2.3. Частотная характеристика с синусоидальным входным сигналом Итак, 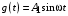 в непрерывном времени. Установившаяся реакция на выходе системы в непрерывном времени. Установившаяся реакция на выходе системы 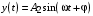 . Тогда отношение . Тогда отношение 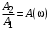 называется амплитудно-частотной характеристикой (АЧХ) системы, а зависимость называется амплитудно-частотной характеристикой (АЧХ) системы, а зависимость 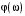 – фазочастотной характеристикой системы (ФЧХ). – фазочастотной характеристикой системы (ФЧХ).Второй путь заключается в использовании преобразований Фурье сигналов на входе и выходе системы. Последние определяются по преобразованиям Лапласа путем замены 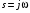 . Если такую замену сделать в передаточной функции системы, придем к понятию комплексной передаточной функции (КПФ) системы . Если такую замену сделать в передаточной функции системы, придем к понятию комплексной передаточной функции (КПФ) системы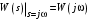 . .Зависимость модуля КПФ от частоты называется амплитудно-частотной характеристикой (АЧХ) системы 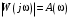 . .Зависимость аргумента КПФ представляет собой фазочастотную характеристику (ФЧХ) системы 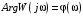 . .Зависимости 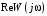 и и 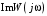 называются вещественно- частотной (ВЧ) и мнимой (МЧ) характеристиками системы соответственно. ВЧХ и АЧХ совместно образуют амплитудно-фазовую характеристику системы (АФХ). Ее выражение следует из выражений ВЧ и МЧ характеристик называются вещественно- частотной (ВЧ) и мнимой (МЧ) характеристиками системы соответственно. ВЧХ и АЧХ совместно образуют амплитудно-фазовую характеристику системы (АФХ). Ее выражение следует из выражений ВЧ и МЧ характеристик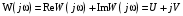 . .АФХ является важнейшей характеристикой системы и часто снимается экспериментальным путем. 2.1.5. Логарифмические частотные характеристики Различают логарифмические амплитудно-частотные характеристики (ЛАЧХ) и логарифмические фазочастотные характеристики (ЛФЧХ). При построении ЛАЧХ и ЛФЧХ частота по оси абсцисс откладывается в логарифмическом масштабе, т. е. на оси наносятся отметки, соответствующие lg, но около отметок указываются действительные значения (рис. 2.4). Рис. 2.4. Ось абсцисс для ЛАФЧХ Начало координат может быть помещено в любой точке оси в зависимости от того, в каком интервале частот находится соответствующий диапазон частот системы. Необходимо помнить, что точка = 0 лежит в и никогда не отмечается на графиках ЛАФЧХ. Равномерной единицей на оси частот является декада – любой отрезок, на котором значение частоты увеличивается в десять раз. Значения частоты откладываются в радианах в секунду (с1). П 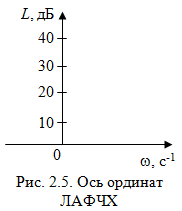 о оси ординат при построении ЛАЧХ откладывается величина о оси ординат при построении ЛАЧХ откладывается величина 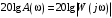 , единицей измерения для которой является децибел (дБ). Обычно логарифмическую амплитуду обозначают через , единицей измерения для которой является децибел (дБ). Обычно логарифмическую амплитуду обозначают через 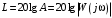 . Ось ординат ЛАЧХ показана на рис. 2.5. Начало оси ординат . Ось ординат ЛАЧХ показана на рис. 2.5. Начало оси ординат 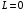 соответствует значению соответствует значению 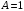 , т. е. равенству амплитуд входного и выходного сигналов системы. Поэтому верхняя полуплоскость ЛАЧХ соответствует значениям , т. е. равенству амплитуд входного и выходного сигналов системы. Поэтому верхняя полуплоскость ЛАЧХ соответствует значениям 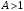 (усиление амплитуды), а нижняя полуплоскость – значениям (усиление амплитуды), а нижняя полуплоскость – значениям 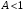 (ослабление амплитуды). (ослабление амплитуды).При построении логарифмической фазочастотной характеристики (ЛФЧХ) частота откладывается на оси абсцисс по-прежнему в логарифмическом масштабе, а значения углов фазового сдвига наносятся на оси ординат в обычном масштабе в угловых градусах. Возможный вид совместно построенных ЛАЧХ и ЛФЧХ показан на рис. 2.6. 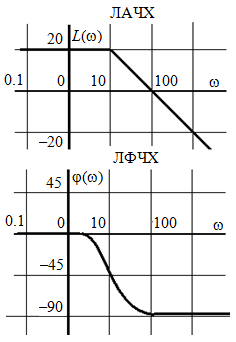 Рис. 2.6. Совместно построенные ЛАЧХ и ЛФЧХ 2.2. Типовые звенья Динамическим звеном называют устройство любого физического вида и конструктивного оформления, представленное определенным дифференциальным уравнением. В соответствии с определением классификация динамических звеньев производится по виду дифференциального уравнения, а именно, по его порядку. Так как одними и теми же дифференциальными уравнениями могут описываться устройства любого типа (электрические, электромеханические, гидравлические, тепловые), то такое предположение позволяет использовать для проектирования различных устройств одинаковые подходы. Любую систему можно представить в виде соединения типовых динамических звеньев. Число таких звеньев невелико и определяется типом нулей и полюсов. Как следует из представления модели в форме пространства состояний, для реализации любой физически осуществимой передаточной функции достаточно двух типов звеньев: интеграторов и усилителей. Если степень числителя передаточной функции m превышает степень знаменателя n, то необходимо звено дифференцирующего типа. В теории управления состав типовых звеньев несколько расширен, исходя из соображения удобства, необходимы звенья, моделирующие часто встречающиеся случаи, а также позволяющие представление передаточных функций общего вида последовательным и параллельным соединением типовых звеньев. Большинство сиcтем может быть представлено совокупностью относительно звеньев с передаточными функциями невысокого порядка. Такие звенья называются типовыми. На рис. 2.7 приведена классификация типовых динамических звеньев. 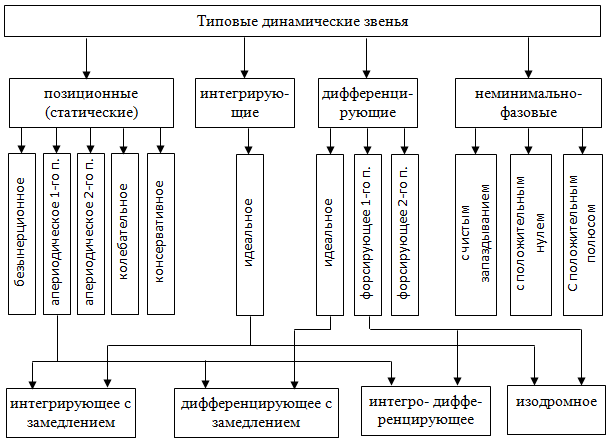 Рис. 2.7. Классификация типовых динамических звеньев Рассмотрим наиболее часто используемые типовые звенья. 2.2.1. Безынерционное звено (П-регулятор) Уравнение движения безинерционного звена имеет вид: 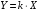 . .Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида: 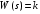 . .Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется как: 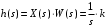 . .Переходная характеристика звена (рис. 2.8, а) определяется как: 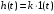 , ,Весовая характеристика (рис. 2.8, б) определяется как: 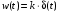 . .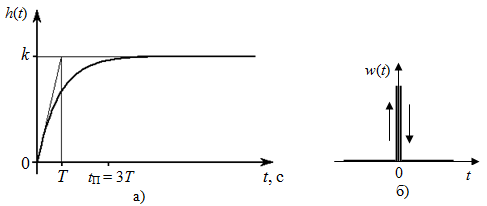 Рис. 2.8. Временные характеристики: а) переходная; б) весовая Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией (рис. 2.9, а) вида: 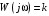 . .Исходя из этого, АЧХ звена – точка на комплексной плоскости (рис. 2.9, б), что следует из выражения: 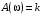 . .ЛЧХ – прямая параллельная оси частот (рис. 2.9, в), следует из выражения: 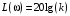 . .ФЧХ – прямая, лежащая на оси частот (рис. 2.9, г), следует из выражения: 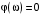 . .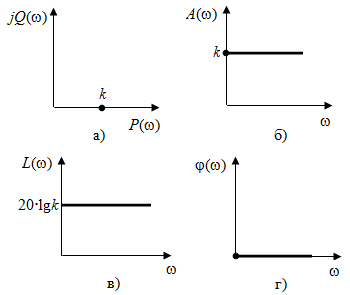 Рис. 2.9. Частотные характериатики: а) АФЧХ; б) АЧХ; в) ЛЧХ; г) ФЧХ 2.2.2. Апериодическое звено первого порядка Уравнение движения для безинерционного звена имеет вид: 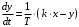 . .Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида: 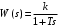 . .Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется как: 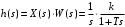 . .Корни характеристического уравнения 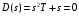 определяются как: определяются как: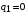 ; ; 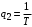 . .Выполняя обратное преобразование изображения переходной характеристики 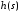 получаем: получаем: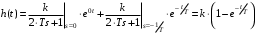 Выполняя аналогичные преобразования над изображением весовой функции 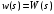 получаем выражение для определения весовой функции 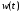 . .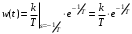 Временные характеристики звена приведены на рис. 2.10. 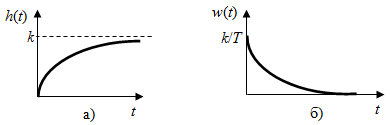 Рис. 2.10. Временные характеристики: а) переходная; б) весовая Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида: 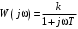 Вещественная 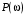 и мнимая и мнимая 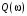 частотные характеристики звена определяются соответственно: частотные характеристики звена определяются соответственно: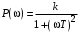 ; ; 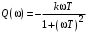 . .АФЧХ звена (рис. 2.11, а) определяется как: 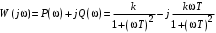 . .АЧХ звена (рис. 2.11, б) определяется как: 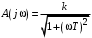 . .ЛЧХ (рис. 2.11, в) определяется как: 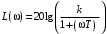 . .Для построения асимптотической ЛАЧХ используется выражение вида: 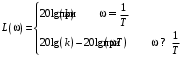 . .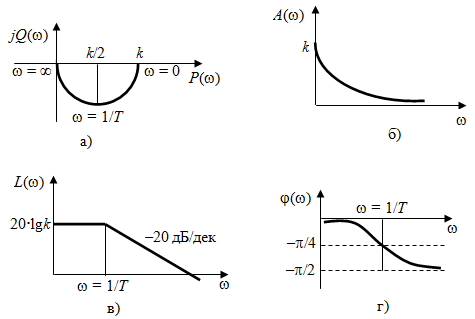 Рис. 2.11. Частотные характеристики: а) АФЧХ; б) АЧХ; в) ЛЧХ; г) ФЧХ ФЧХ (рис. 2.11, г) определяется как: 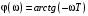 . .2.2.3. Апериодическое звено второго порядка Уравнение движения для колебательного звена имеет вид:
где 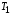 , , 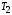 – постоянные времени звена. – постоянные времени звена.Выполняя преобразование Лапласа над уравнением (2.5), получаем выражение для передаточной функции звена следующего вида:
Характеристическое уравнение имеет вид:
В зависимости от значений 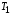 и и 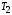 уравнения (2.7) аппериодическое звено второго порядка имеет различный вид и три различных названия: уравнения (2.7) аппериодическое звено второго порядка имеет различный вид и три различных названия:а) апериодическое звено второго порядка; б) колебательное звено второго порядка; в) консервативное звено. Апериодическое звено второго порядка. Если в уравнении (2.5) выполняется неравенство 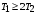 , то корни вещественные и равны: , то корни вещественные и равны: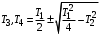 – новые постоянные времени. – новые постоянные времени.Тогда передаточная функция (2.6) примет вид:
Из (2.8) видно, что апериодическое звено второго порядка – это комбинация двух апериодических звеньев первого порядка. Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Переходная характеристика звена (рис. 2.12, а) определяется как: 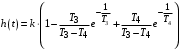 Весовая характеристика звена (рис. 2.12, б) определяется как: 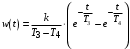 . .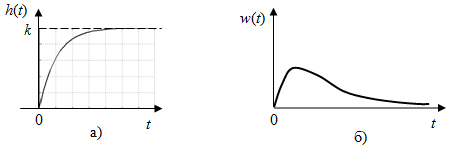 Рис. 2.12. Временные характеристики: а) переходная; б) весовая Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида: 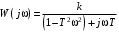 . .Вещественная 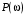 и мнимая и мнимая 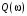 частотные характеристики звена определяются соответственно: частотные характеристики звена определяются соответственно: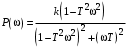 ; ; 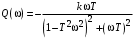 . .АФЧХ звена (рис. 2.13, а) определяется как: 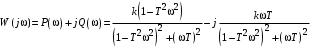 . .АЧХ звена (рис. 2.13, б) определяется как: 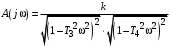 . .ЛЧХ (рис. 2.11, в) определяется как: 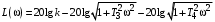 . .ФЧХ (рис. 2.13, г) определяется как: 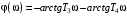 . .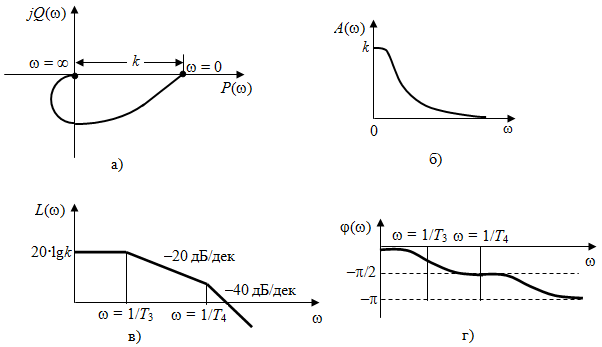 Рис. 2.13. Частотные характеристики: а) АФЧХ; б) АЧХ; в) ЛЧХ; г) ФЧХ Колебательное звено второго порядка. Если в уравнении (2.5) выполняется неравенство 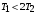 , то корни корни характеристического уравнения комплексные и уравнение (2.7) запишется в виде: , то корни корни характеристического уравнения комплексные и уравнение (2.7) запишется в виде: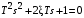 , ,где 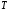 – постоянная времени, определяющая угловую частоту свободных колебаний – постоянная времени, определяющая угловую частоту свободных колебаний 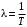 ; ;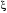 – коэффициент затухания, лежащий в пределах – коэффициент затухания, лежащий в пределах 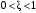 . .Передаточная функция (2.6) запишется в виде: 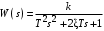 . .Переходная характеристика запишется в виде:
где 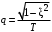 , , 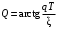 . .Из (2.9) видно, что ПХ зависит коэффициента затухания (рис. 2.14). 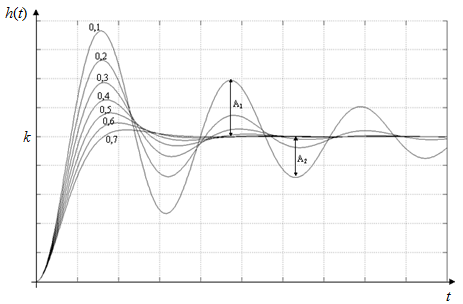 Рис. 2.14. Переходные характеристики для 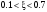 ФЧХ представлена на рис. 2.15. 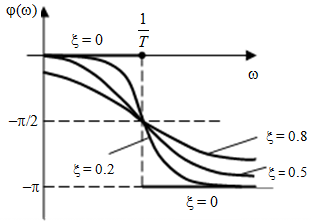 Рис. 2.15. ФЧХ для 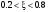 Консервативное звено. Консервативно звено является частным случаем колебательного звена при 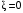 . .Передаточная функция (2.6) запишется в виде: 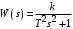 . .Переходная функция: 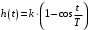 . .Весовая функция: 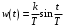 . .Таким образом, временные характеристики (рис. 2.15) соответствуют незатухающим колебаниям с угловой частотой 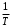 . .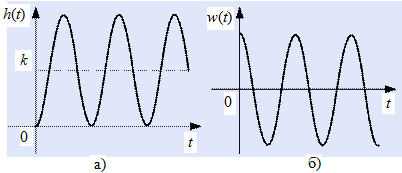 Рис. 2.15. Временные характеристики: а) переходная; б) весовая 2.2.4. Интегрирующее звено (И-регулятор) Уравнение движения для интегрирующего звена имеет вид: 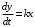 . . Выполняя над этим уравнением преобразование Лапласа получим выражение для передаточной функции звена следующего вида: 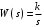 Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Переходная характеристика звена (рис. 2.16, а) определяется как 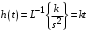 . .Весовая характеристика (рис. 2.16, б) определяется как: 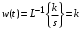 . .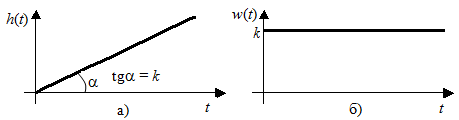 Рис. 2.16. Переходная и весовая характеристики Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функции вида: 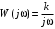 . .Вещественная 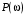 и мнимая и мнимая 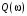 частотные характеристики звена (рис. 2.17, а) определяются как: частотные характеристики звена (рис. 2.17, а) определяются как: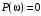 , ,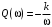 . .АЧХ звена (рис. 2.17, б) определяется как: 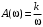 . .ЛАЧХ определяется как: 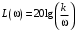 . .Для построения асимптотической ЛАЧХ (рис. 2.17, в) воспользуемся выражением вида: 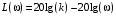 . .ФЧХ (рис. 2.17, г) определяется как: 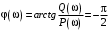 . .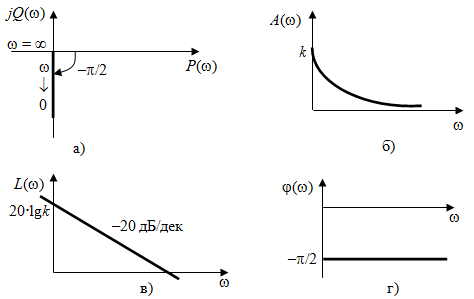 Рис. 2.17. Частотные характеристики: а) АФЧХ; б) АЧХ; в) ЛЧХ; г) ФЧХ 2.2.5. Дифференцирующее звено (Д-регулятор) Уравнение движения для дифференцирующего звена имеет вид 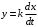 . .Выполнив преобразование Лапласа получим выражение для передаточной функции звена следующего вида: 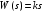 . .Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Переходная характеристика дифференцирующего звена (рис. 2.18, а) определяется как: 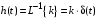 , ,весовая характеристика (рис. 2.18, б) запишется как: 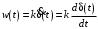 . . 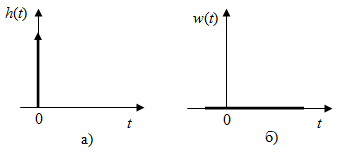 Рис. 2.18. Временные характеристики: а) переходная; б) весовая Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида: 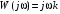 . .Вещественная 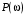 и мнимая и мнимая 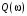 частотные характеристики звена (рис. 2.19, а) определяются как: частотные характеристики звена (рис. 2.19, а) определяются как: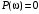 ; ;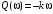 . .АЧХ звена (рис. 2.19, б) определяется как: 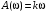 . .ЛАЧХ звена определяется как: 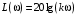 . .Для построения асимптотической ЛАЧХ (рис. 2.19, в) воспользуемся выражением вида: 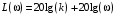 . .ФЧХ звена (рис. 2.19, г) определяется как: 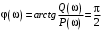 . .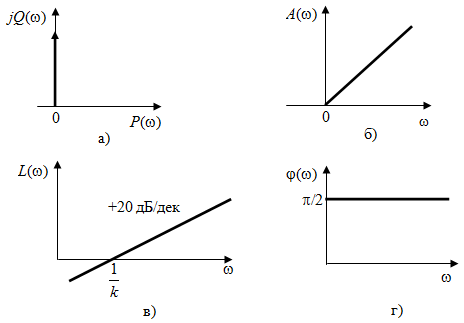 Рис. 2.19. Частотные характеристики: а) АФЧХ; б) АЧХ; в) ЛЧХ; г) ФЧХ 2.3. Структурные схемы Структурной схемой САУ называется графическая форма представления математической модели системы в виде соединения отдельных звеньев, каждое из которых задано каким-либо математическим оператором преобразования входного сигнала в выходной. Операторы преобразования могут быть заданы символами преобразования во временной области или в области изображений (передаточные функции) или с помощью статических и динамических характеристик. Звенья представляются на структурных схемах с помощью прямоугольников. Соединение их осуществляется стрелками, указывающими направления передачи сигналов управления. Прохождение сигналов управления против направления, указанного стрелками, невозможно. 2.3.1. Преобразование структурных схем Преобразование структурных схем линейных непрерывных систем управления базируется на выполнении двух важнейших принципов линейных преобразований: 1) аддитивности или суперпозиции (наложения) и 2) коммутативности (перестановки местами). Преобразование структурных схем формулируется в виде правил преобразований, поэтому далее будем рассмотрено совокупность таких правил. Последовательное соединение звеньев На структурной схеме (рис. 2.20) представлено последовательное соединение звеньев. 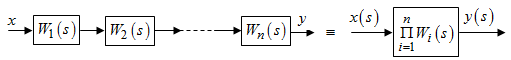 Рис. 2.20. Структурная схема последовательно соединенных звеньев Передаточная функция запишется в виде: 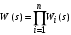 Правило: Передаточная функция последовательного соединения звеньев равна произведению передаточных функций отдельных звеньев. Параллельные соединения звеньев На структурной схеме (рис. 2.21) представлено параллельное соединение звеньев. 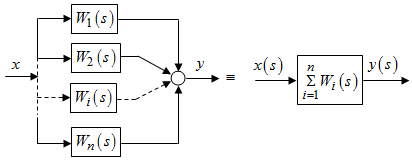 Рис. 2.21. Структурная схема параллельно соединенных звеньев Передаточная функция запишется в виде: 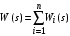 . .Правило: Передаточная функция параллельного соединения непрерывных звеньев равна сумме их передаточных функций. Соединение с обратной связью На структурной схеме (рис. 2.22) представлено соединение звеньев с обратной связью. 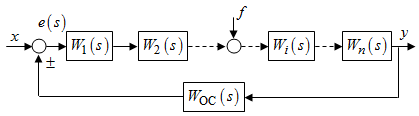 Рис. 2.22. Структурная схема соединенных звеньев с обратной связью Сигнал на выходе элемента сравнения:  Выходной сигнал соединения: 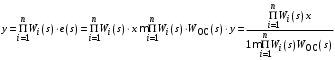 . .Передаточная функция замкнутого контура по управлению: 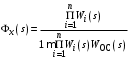 . .Если обратная связь единичная, тогда: 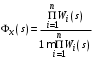 . .Передаточная функция замкнутого контура по возмущению: 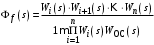 . .Перестановка местами звеньев структурной схемы - Перестановка местами динамических звеньев На рис. 2.23 показан варинт перестановки местами динамических звеньев. Рис. 2.23. Вариант перестановки местами динамических звеньев Правило: В любой последовательной цепи непрерывных динамических звеньев их можно менять местами в произвольном порядке. Перестановка местами узлов суммирования и динамических звеньев На рис. 2.24 показан варинт перестановки местами узлов суммирования и динамических звеньев. 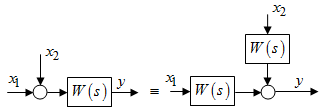 Рис. 2.24. Вариант перестановки местами узлов суммирования и динамических звеньев Правило: При переносе узла суммирования через динамическое звено необходимо включить в подходящее к узлу ветви звенья с передаточной функцией звена. Перестановка местами узлов разветвления и других звеньев структурной схемы Правило: при переносе узла разветвления сигналов через динамическое звено необходимо в отходящие от узла ветви добавить звенья с передаточной функцией звена, если перенос выполняется против направления передачи сигналов управления (рис. 2.25, а), и звенья с обратной передаточной функцией, если перенос происходит по направлению передачи сигналов управления (рис. 2.25, б).  Рис. 2.25. Варианты переноса узла разветвления через динамическое звено Инверсия направления прямого пути Правило: В любом непрерывном прямом пути можно поменять направление передачи сигналов управления, поменяв на обратные передаточные функции звеньев пути и поменяв на обратные знаки суммирования внешних сигналов (рис. 2.26).  Рис. 2.26. Инверсия направления прямого пути Инверсия замкнутого контура Правило: В любом замкнутом непрерывном контуре можно поменять местами прямой и обратный каналы, заменив их передаточные функции на обратные и заменив на обратные знаки суммирования внешних сигналов, кроме основного узла суммирования. Это правило получается после двукратного применения правила инверсии пути к прямому и обратному каналам контура. Рис. 2.27. иллюстрирует результат инвертирования контура. 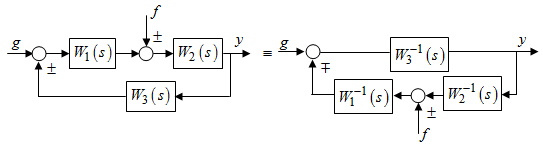 Рис. 2.27. Инверсия замкнутого контура 2.3.2. Детализированные структурные схемы Кроме общих структурных схем широко используются детализированные структурные схемы, состоящие только из безинерционных масштабных звеньев и идеальных интегрирующих звеньев с полностью вскрытыми связями между ними. Детализированная структурная схема (ДСС) составляется из исходной общей схемы путем преобразования звеньев с так называемыми «сложными» передаточными функциями. «Детализация» звена со «сложной» передаточной функцией осуществляется в следующей последовательности: записывается операторное уравнение звена по исходной передаточной функции. 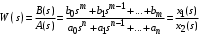 , m , m 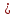 n. n.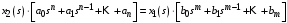 ; ; 2) Уравнение разрешается относительно старшей производной выходной величины 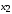 : :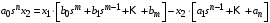 ; ;3) Обе части уравнения делятся на коэффициент при x2 в левой части с целью получить выражение для x2 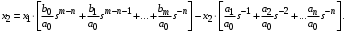 Пользуясь указанной последовательностью удается легко построить ДСС для звеньев с передаточными функциями невысокого порядка (n 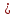 2). 2).В случае исходной передаточной функции с n > 2 целесообразно пользоваться процедурой, называемой непосредственной декомпозицией. Суть ее заключается в том, что вводится фиктивная переменная x(s) и на нее умножается числитель и знаменатель передаточной функции: 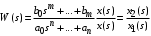 . .Приравнивание числителя и знаменателя дает
Последнее выражение используется для определения x(s) путем записи его относительно старшей производной с последующим делением на коэффициент при старшей производной: 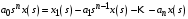 , ,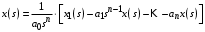 . .После определения 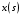 строится схема вычисления строится схема вычисления 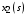 согласно выражения (2.10). Общая схема ДСС "сложного" звена представлена на рис. 2.28. согласно выражения (2.10). Общая схема ДСС "сложного" звена представлена на рис. 2.28.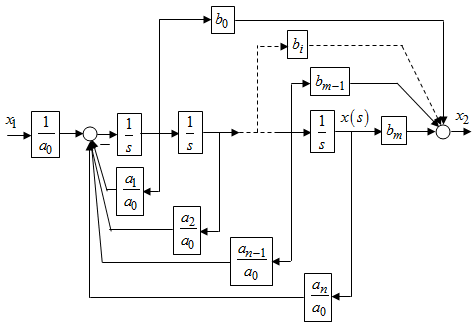 Рис. 2.28. Общая схема ДСС Проиллюстрируем на примерах. Пример 1: Построить ДСС звена с передаточной функцией 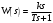 , иначе можно записать как , иначе можно записать как 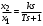 . .Выполнив последовательно преобразования: 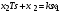 ; ; 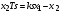 , ,получим в математическом виде: 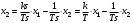 , ,или в графическом виде (рис. 2.29): 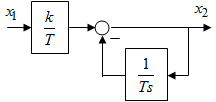 Рис. 2.29. ДСС звена 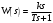 Пример 2: Построить ДСС стандартного звена 2-го порядка с передаточной функцией 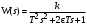 , иначе можно записать как , иначе можно записать как 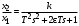 . .Выполнив последовательно преобразования: 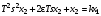 ; ;получим в математическом виде: 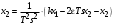 , ,или в графическом виде (рис. 2.30): 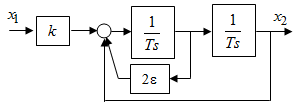 Рис. 2.30. ДСС звена 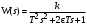 В заключении отметим, что ДСС непрерывных систем нашли широкое применение для составления уравнений состояния, а также для составления и расчета параметров модели при аналоговом моделировании. Вопросы для самопроверки Каково назначение математического описания систем? Что такое динамика системы? Чем отличается математическое описание динамики системы от описания ее статики? Что представляет собой условие физической реализуемости системы? Каким образом линеаризуются дифференциальные уравнения? Назовите формы записи линеаризованных уравнений. Каким образом перейти к первой форме записи дифференциального уравнения звена? Как в этом случае называются коэффициенты? Как перейти от дифференциального уравнения к операторному? Дайте определение передаточной функции. Как по дифференциальному уравнению звена найти его передаточную функцию? Что такое динамическое звено и его характеристика? Дайте определение основных характеристик. Какие частотные характеристики используются для исследования систем? Почему ЛЧХ нашли большое применение в инженерной практике? По каким признакам классифицируются типовые динамические звенья? Перечислите группы основных типов звеньев. Что представляет собой структурная схема системы управления? Какие способы соединений звеньев используются в системах? Как находятся передаточные функции смешанных соединений звеньев? Каким образом строятся логарифмические частотные характеристики разомкнутой цепи звеньев? Постройте ЛЧХ типовых звеньев. 3. АНАЛИЗ ЛИНЕЙНЫХ САУ 3.1. Устойчивость линейных непрерывных систем управленияУстойчивость систем автоматического управления является важнейшей характеристикой их работоспособности. Неустойчивая система является неработоспособной. Обеспечение устойчивой работы проектируемой или создаваемой системы управления является первоочередной задачей разработчика этой системы. Под устойчивостью линейной системы понимается свойство затухания переходных процессов во всех элементах системы с течением времени. Если представить реакцию системы на входной сигнал как сумму вынужденной (установившейся) составляющей и переходной (свободной) составляющей 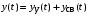 , ,то условие устойчивости формируется следующим образом: 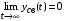 . .Если 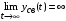 , то система неустойчива. , то система неустойчива. 3.1.1. Общее условие устойчивости Из анализа переходных составляющих выходной величины системы для различных корней характеристического уравнения системы следует, что условия устойчивости, сформулированные выше, выполняются, если все корни имеют отрицательные вещественные части. В частном случае вещественных корней они должны быть отрицательными. Только в этом случае все переходные составляющие будут стремиться с течением времени к нулю. Таким образом, для непрерывных систем общим условием устойчивости является нахождение всех корней характеристического уравнения замкнутой системы в левой полуплоскости плоскости корней (рис. 3.1). Е 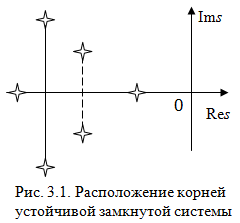 сли хотя бы один корень окажется в правой полуплоскости, система будет неустойчивой. Мнимая ось плоскости s является границей устойчивости. Причем, если сли хотя бы один корень окажется в правой полуплоскости, система будет неустойчивой. Мнимая ось плоскости s является границей устойчивости. Причем, если 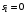 , граница устойчивости называется апериодической. Если , граница устойчивости называется апериодической. Если 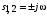 (чисто мнимые корни, равноудаленные от начала координат), то граница устойчивости называется колебательной, так как система в этом случае совершает незатухающие колебания, постоянной амплитуды и частоты, равной . (чисто мнимые корни, равноудаленные от начала координат), то граница устойчивости называется колебательной, так как система в этом случае совершает незатухающие колебания, постоянной амплитуды и частоты, равной .3.1.2. Критерии устойчивости Вычисление корней уравнения, особенно высокой степени, затруднительно. Поэтому были разработаны критерии, позволяющие делать заключение об устойчивости системы без определения корней характеристического уравнения. Различают два вида критериев устойчивости: 1) алгебраические; 2) частотные. Критерии первого вида формируют ограничения на коэффициенты характеристического уравнения. Критерии второго вида базируются на анализе прохождения частотных характеристик замкнутой или разомкнутой системы. 3.1.2.1. Алгебраические критерии устойчивости Среди алгебраических критериев непрерывных систем наибольшее применение получили критерии Гурвица и Рауса. Рассмотрим их в указанной последовательности. Критерий Гурвица Из коэффициентов характеристического уравнения замкнутой системы: 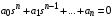 составляется таблица, называемая матрицей Гурвица по следующему правилу: 1) по диагонали сверху вниз записываются все коэффициенты, начиная с 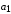 до до 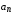 в порядке возрастания индексов; в порядке возрастания индексов;2) столбцы дополняются вверх коэффициентами с возрастающими индексами, вниз коэффициентами с убывающими индексами; 3) на месте коэффициентов с индексами больше n и меньше нуля проставляются нули.  Сам критерий формируется следующим образом: для устойчивости замкнутой системы необходимо и достаточно, чтобы при 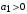 были положительными n главных диагональных определителя матрицы Гурвица. были положительными n главных диагональных определителя матрицы Гурвица.Главные определители матрицы Гурвица имеют вид: 1 = a1, 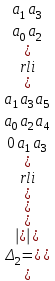 и так далее. и так далее.Частные случаи. 1. Система 1-го порядка, характеристическое уравнение которой 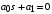 , устойчива, если , устойчива, если 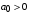 и и 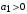 , т. е. Если оба коэффициента характеристического уравнения положительны. , т. е. Если оба коэффициента характеристического уравнения положительны.2. Система 2-го порядка (характеристическое уравнение 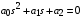 ) устойчива, если ) устойчива, если 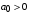 , , 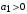 и и 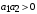 , т. е. Если все три коэффициента положительны. , т. е. Если все три коэффициента положительны.3. Положительность коэффициентов характеристического уравнения является необходимым, но недостаточным условием устойчивости системы любого порядка. 4. Наличие хотя бы одного отрицательного коэффициента является признаком неустойчивого состояния системы. 5. Равенство нулю свободного коэффициента 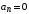 , означает, что система находится на границе устойчивости. , означает, что система находится на границе устойчивости.6. Равенство нулю любого другого коэффициента свидетельствует либо о неустойчивости системы, либо о нахождении ее на границе устойчивости. Критерий Гурвица удобен не только для проверки устойчивости замкнутой системы. С его помощью легко выясняется влияние того или иного параметра системы на ее устойчивость, а также легко определяются границы значений параметра, в которых система остается устойчивой. Критерий Рауса При использовании критерия Рауса для проверки устойчивости замкнутой системы составляется таблица Рауса (табл. 3.1). Она содержит n + 1 строк и число столбцов, равное числу четных коэффициентов характеристического уравнения. В первой строке записываются коэффициенты с четными индексами, начиная с 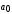 , во второй – коэффициенты с нечетными индексами, начиная с , во второй – коэффициенты с нечетными индексами, начиная с 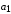 . Любой из остальных элементов таблицы определяется по выражению . Любой из остальных элементов таблицы определяется по выражению 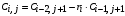 , где , где 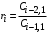 ; i – номер строки, j – номер столбца таблица Рауса. ; i – номер строки, j – номер столбца таблица Рауса. |

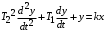 ,
,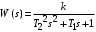 .
.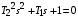 .
.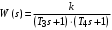 .
.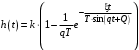 ,
,