Таблица 3.1.
Коэффициенты 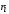
|
i
| Номер столбца |
1
|
2
|
3
|
|
–
|
1
|
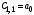
|
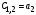
|
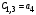
|
|
–
|
2
|
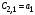
|
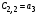
|
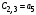
|
|
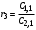
|
3
|
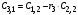
|
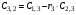
|
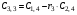
|
|
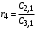
|
4
|
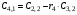
|
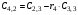
|
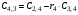
|
|
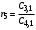
|
5
|
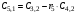
|
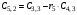
|
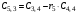
|
|
|
|
|
|
|
|
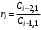
|
i
|
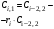
|
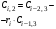
|
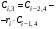
|
|
|
|
|
|
|
|
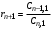
|
n+1
|
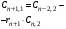
|
Не составляются
|
Критерий устойчивости Рауса формируется следующим образом.
Для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы элементы первого столбца таблицы Рауса были положительны.
При наличии отрицательных элементов в 1-ом столбце система будет неустойчивой. Число таких элементов равно числу корней характеристического уравнения, находящихся в правой полуплоскости плоскости s.
Если один из элементов первого столбца равен нулю, а остальные элементы положительны, то система будет находиться на границе устойчивости колебательного типа (характеристическое уравнение будет иметь пару чисто мнимых корней).
Если равен нулю (n +1)-элемент или равны нулю k последних элементов 1-го столбца, система также будет находиться на границе устойчивости, а характеристическое уравнение будет иметь один или kнулевых корней.
Таблица и критерий Рауса положены в основу алгоритма и программы проверки устойчивости в ряде компьютерных пакетов анализа моделей различных систем.
3.1.2.2. Частотные критерии устойчивости
Среди частотных критериев устойчивости, используемых в практике анализа устойчивости непрерывных и дискретных систем автоматического управления, наибольшее признание получили критерий годографа характеристического полинома замкнутой системы (известный в отечественной литературе как критерий Михайлова) и критерий Найквиста, обеспечивающий определение устойчивости по виду частотных характеристик разомкнутой системы.
В основу названных выше критериев положено следствие из известного в теории функции комплексной переменной принципа аргумента. Оно устанавливает соответствие между числом корней в левой и правой полуплоскости и суммарным приращением аргумента вектора характеристического полинома замкнутой системы, при изменении частоты в диапазоне 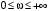 . Рассмотрим это соответствие. . Рассмотрим это соответствие.
Характеристическое уравнение замкнутой непрерывной системы:
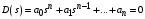 , ,
где левая часть уравнения 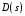 называется характеристическим полиномом. Его можно представить в соответствии с теоремой Безу следующим образом: называется характеристическим полиномом. Его можно представить в соответствии с теоремой Безу следующим образом: 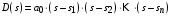 , ,
г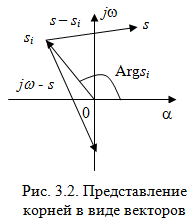 де де  ( ( ) – корни характеристического уравнения ) – корни характеристического уравнения 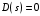 ; ; 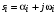 . На комплексной плоскости каждый корень может быть представлен вектором (рис. 3.2). Длина вектора . На комплексной плоскости каждый корень может быть представлен вектором (рис. 3.2). Длина вектора 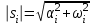 , угол поворота от положительной вещественной полуоси равен аргументу , угол поворота от положительной вещественной полуоси равен аргументу 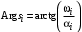 . Отдельные сомножители . Отдельные сомножители 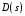 вида вида 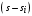 могут быть представлены векторами, проведенными из точек могут быть представлены векторами, проведенными из точек 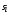 в точке в точке  . .
Положим 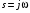 , тогда вектор , тогда вектор 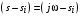 будет скользить своим концом по мнимой оси при изменении частоты будет скользить своим концом по мнимой оси при изменении частоты 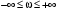 . .
Приращение аргумента
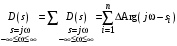 , ,
причем корень 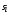 , расположенный в левой полуплоскости, обеспечивает приращение аргумента +(рис. 3.3, а), а корень, находящийся в правой полуплоскости, дает , расположенный в левой полуплоскости, обеспечивает приращение аргумента +(рис. 3.3, а), а корень, находящийся в правой полуплоскости, дает 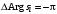 (рис. 3.3, б). (рис. 3.3, б).
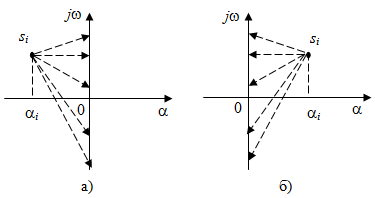
Рис. 3.3. Приращение аргумента в зависимости от расположения корней
Если общее число корней характеристического уравнения n, а в правой полуплоскости находится m корней, то суммарное приращение аргумента 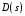 : :
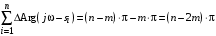 . .
Если изменять частоту только в положительном диапазоне 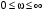 , то суммарное приращение аргумента , то суммарное приращение аргумента 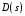 будет в 2 раза меньше: будет в 2 раза меньше:
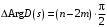 . .
Полученное соотношение положено в основу частотных критериев устойчивости непрерывных систем.
Критерий годографа характеристического полинома
На основании полученного в предыдущем параграфе соотношения для непрерывных систем и полагая, что в правой полуплоскости нет ни одного корня (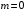 ), находим, что ), находим, что
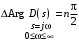 . .
Отсюда вытекает следующая формулировка критерия.
Для устойчивости замкнутой непрерывной системы необходимо и достаточно, чтобы при изменении частоты в диапазоне  годограф характеристического полинома начинался на положительной вещественной оси и обошел в положительном направлении (против часовой стрелки) последовательно n квадрантов, нигде не обращаясь в нуль и нигде не пересекаясь сам с собой. годограф характеристического полинома начинался на положительной вещественной оси и обошел в положительном направлении (против часовой стрелки) последовательно n квадрантов, нигде не обращаясь в нуль и нигде не пересекаясь сам с собой.
Годографы устойчивых систем показаны на рис. 3.4, а, для неустойчивых систем на рис. 3.4, б.
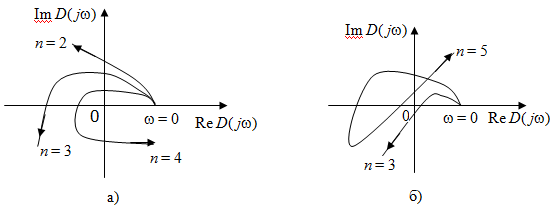
Рис. 3.4. Годографы: а) устойчивых систем; б) неустойчивых систем
Если систем находится на границе устойчивости, то годограф  проходит через начало координат. проходит через начало координат.
Критерий Найквиста
Критерий Найквиста позволяет оценивать устойчивость замкнутой системы автоматического управления по частотным характеристикам разомкнутой системы. В качестве частотных характеристик используется амплитудно-фазовая (АФХ) характеристика и ЛАФЧХ разомкнутой системы.
Рассмотрим сначала критерий Найквиста на базе АФХ разомкнутой системы.
Пусть передаточная функция разомкнутой системы
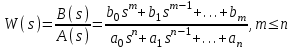 . .
Передаточная функция замкнутой системы
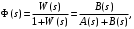
где 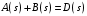 характеристический полином замкнутой системы. характеристический полином замкнутой системы.
Рассмотрим вспомогательную функцию
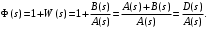
Заметим, что числитель 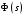 равен равен 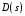 характеристическому полиному замкнутой системы, а знаменатель характеристическому полиному замкнутой системы, а знаменатель 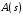 характеристический полином разомкнутой системы. Заметим также, что степени числителя и знаменателя равны, так как m n. характеристический полином разомкнутой системы. Заметим также, что степени числителя и знаменателя равны, так как m n.
Предположим, что разомкнутая система устойчива, т. е. все корни 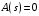 лежат в левой полуплоскости. Для того, чтобы и замкнутая система была устойчивой, необходимо, чтобы все корни лежат в левой полуплоскости. Для того, чтобы и замкнутая система была устойчивой, необходимо, чтобы все корни 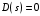 находились также в левой полуплоскости. находились также в левой полуплоскости.
Положим 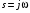 и будем изменять от 0 до . Согласно принципа аргумента и будем изменять от 0 до . Согласно принципа аргумента
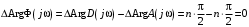 . .
Это значит, что годограф вспомогательной функции 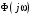 при при 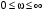 не будет охватывать начало координат (рис. 3.5, а). Заметим, что комплексная передаточная функция разомкнутой системы отличается от не будет охватывать начало координат (рис. 3.5, а). Заметим, что комплексная передаточная функция разомкнутой системы отличается от 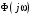 на единицу на единицу
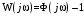 . .
Поэтому вместо 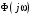 можно рассматривать можно рассматривать 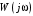 , но в координатах, где мнимая ось перенесена на (1) (рис. 3.5, б). , но в координатах, где мнимая ось перенесена на (1) (рис. 3.5, б).
Отсюда следует формулировка критерия Найквиста для случая устойчивой разомкнутой системы.
Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала критическую точку с координатами (1, j0).
Рис. 3.5. Годограф вспомогательной функции:
а) не охватывающей начало координат; б) охватывающей начало координат
На рис. 3.6 показаны различные случаи прохождения АФХ разомкнутой системы относительно критической точки 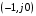 , штриховыми линиями показаны АФХ при уменьшении коэффициента усиления разомкнутых систем. , штриховыми линиями показаны АФХ при уменьшении коэффициента усиления разомкнутых систем.
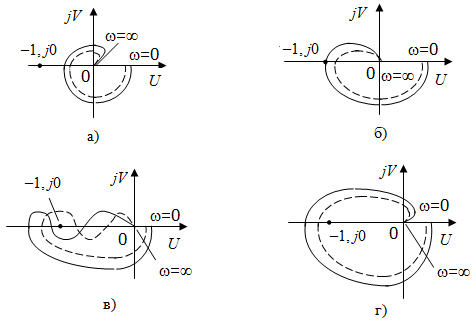
Рис. 3.6. Примеры прохождения АФХ: а) – абсолютно устойчивая система; б) – система на границе устойчивости; в) – условно устойчивая система, которая при уменьшении коэффициента усиления может стать неустойчивой; г) – неустойчивая система
Для астатических систем (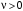 ) применение критерия Найквиста имеет свою особенность. Дело в том, что АФХ таких систем в области низких, частот приближаются к одной из осей комплексной плоскости. Поэтому для определения устойчивости по критерию Найквиста необходимо предварительно дополнять АФХ дугами ) применение критерия Найквиста имеет свою особенность. Дело в том, что АФХ таких систем в области низких, частот приближаются к одной из осей комплексной плоскости. Поэтому для определения устойчивости по критерию Найквиста необходимо предварительно дополнять АФХ дугами 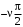 окружности бесконечно большого радиуса (рис. 3.7). окружности бесконечно большого радиуса (рис. 3.7).
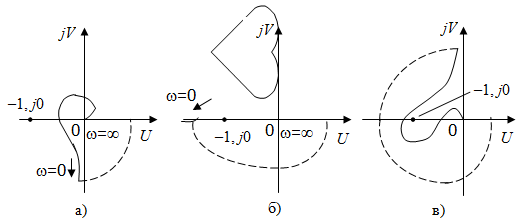
Рис. 3.7. Устойчивость системы: а) устойчивая; б) неустойчивая; в) условно устойчивая
Теперь предположим, что разомкнутая система не устойчива, т. е. l корней характеристического уравнения находятся в правой полуплоскости.
Тогда при изменении частоты от 0 до суммарное приращение аргумента будет:
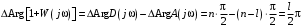 . .
Отсюда формулировка критерия Найквиста.
Е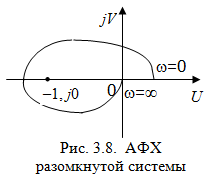 сли разомкнутая система неустойчива, то для того, чтобы была устойчивой замкнутая система, необходимо и достаточно, чтобы АФХ разомкнутой системы охватывала критическую точку в положительном направлении сли разомкнутая система неустойчива, то для того, чтобы была устойчивой замкнутая система, необходимо и достаточно, чтобы АФХ разомкнутой системы охватывала критическую точку в положительном направлении 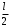 раз, где l – число корней характеристического уравнения разомкнутой системы в правой полуплоскости. раз, где l – число корней характеристического уравнения разомкнутой системы в правой полуплоскости.
На рис. 3.8 показана АФХ разомкнутой системы, имеющая два корня в правой полуплоскости. Система, имеющая такую АФХ, будет устойчивой в замкнутом состоянии.
При сложной форме АФХ определить число охватов критической точки (1, j0) затруднительно. В этом случае удобнее считать число переходов АФХ через отрезок (, 1) отрицательной вещественной оси. Переход сверху вниз считается положительным, снизу вверх – отрицательным. Если АФХ начинается на отрезке (, 1) при = 0 и заканчивается на нем при = , то считается, что она совершает 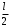 перехода. перехода.
Формулировка критерия Найквиста по числу переходов будет следующей.
Е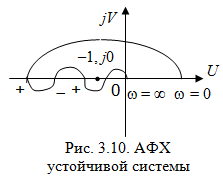 сли разомкнутая система неустойчива, то для того, чтобы разность между числами положительных и отрицательных переходов АФХ разомкнутой системы через отрезок вещественной оси (, 1) была равна сли разомкнутая система неустойчива, то для того, чтобы разность между числами положительных и отрицательных переходов АФХ разомкнутой системы через отрезок вещественной оси (, 1) была равна 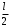 , где l – число корней разомкнутой системы в правой полуплоскости. , где l – число корней разомкнутой системы в правой полуплоскости.
Так система, АФХ которой показана на рис. 3.10, будет устойчивой, если число корней в правой полуплоскости l = 2.
Р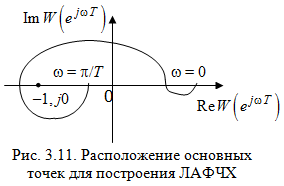 ассмотрим теперь, как будет формироваться критерий Найквиста с использованием логарифмических амплитудно-частотных фазочастотных характеристик. Прежде всего установим, где будет расположена критическая точка с координатами ассмотрим теперь, как будет формироваться критерий Найквиста с использованием логарифмических амплитудно-частотных фазочастотных характеристик. Прежде всего установим, где будет расположена критическая точка с координатами 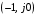 в плоскости АФХ разомкнутой системы. Отметим, что критической точке в плоскости АФХ разомкнутой системы. Отметим, что критической точке 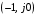 соответствует точка, в которой модуль вектора АФХ соответствует точка, в которой модуль вектора АФХ 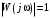 , а угол сдвига , а угол сдвига 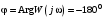 рис. 3.11. рис. 3.11.
В плоскости ЛАФЧХ этой точке соответствует частота, на которой 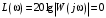 , т. е. график , т. е. график 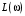 пересекает ось частот, и пересекает ось частот, и
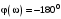 , т. е. график , т. е. график 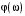 пересекает линию (180). Таким образом, если замкнутая система будет находиться на границе устойчивости, то ЛАЧХ и ЛФЧХ разомкнутой системы пересекают линии пересекает линию (180). Таким образом, если замкнутая система будет находиться на границе устойчивости, то ЛАЧХ и ЛФЧХ разомкнутой системы пересекают линии 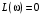 и и
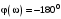 одновременно, на одной и той же частоте (рис. 3.12). одновременно, на одной и той же частоте (рис. 3.12).
Если же система устойчива в разомкнутом и замкнутом состояниях, то ее АФХ проходит справа от критической точки, т. е. 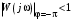 . .
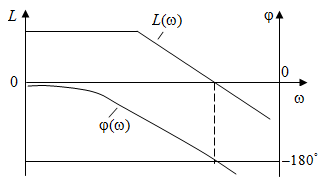
Рис. 3.12. ЛАЧХ системы, стоящей на границы устойчивости
Отсюда следует первая формулировка критерия Найквиста по ЛАФЧХ разомкнутой системы: если разомкнутая система устойчива, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы ЛАЧХ системы пересекала ось частот раньше, чем ЛФЧХ пересечет линию 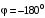 . .
Иллюстрация взаимного расположения ЛАЧХ и ЛФЧХ разомкнутой системы, устойчивой в замкнутом состоянии, показана на рис. 3.13.
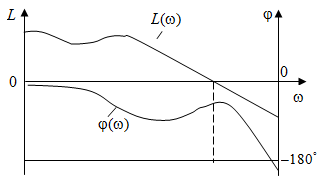
Рис. 3.13. ЛАЧХ и ЛФЧХ разомкнутой системы устойчивой в замкнутом состоянии
При сложной форме АФХ и ЛАФЧХ может иметь место неоднократное пересечение линии 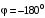 характеристикой характеристикой 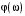 на участке частот, где на участке частот, где 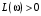 , т. е. до точки пересечения , т. е. до точки пересечения 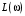 оси частот. То же явление может наблюдаться и в плоскости ЛАФЧХ системы, неустойчивой в разомкнутом состоянии. В этом случае проще делать заключение о том, устойчива система или нет в замкнутом состоянии по числу, переходов графика оси частот. То же явление может наблюдаться и в плоскости ЛАФЧХ системы, неустойчивой в разомкнутом состоянии. В этом случае проще делать заключение о том, устойчива система или нет в замкнутом состоянии по числу, переходов графика 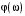 через линию через линию 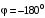 левее точки пересечения графиком левее точки пересечения графиком 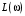 оси частот (рис. 3.14). оси частот (рис. 3.14).
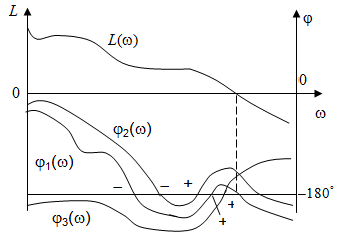
Рис. 3.14. Определение устойчивости по переходу графика ФЧХ
Формулировка критерия Найквиста в этом случае следующая: для –устойчивости замкнутой системы необходимо и достаточно, чтобы при положительных значениях ЛАЧХ разность между числом положительных и отрицательных переходов ФЧХ через линию 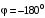 равнялась равнялась 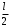 , где l – число корней, расположенных в правой полуплоскости. Положительным считается переход ФЧХ линии , где l – число корней, расположенных в правой полуплоскости. Положительным считается переход ФЧХ линии 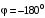 снизу вверх, отрицательным – сверху вниз. Характеристика снизу вверх, отрицательным – сверху вниз. Характеристика 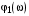 соответствует системе, устойчивой в разомкнутом состоянии и находящейся на границе устойчивости в замкнутом состоянии. Характеристика соответствует системе, устойчивой в разомкнутом состоянии и находящейся на границе устойчивости в замкнутом состоянии. Характеристика 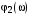 принадлежит системе устойчивой в разомкнутом и замкнутом состояниях. И, наконец, принадлежит системе устойчивой в разомкнутом и замкнутом состояниях. И, наконец, 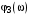 свидетельствует о неустойчивости в разомкнутом состоянии и устойчивости в замкнутом, если число неустойчивых корней l= 2. свидетельствует о неустойчивости в разомкнутом состоянии и устойчивости в замкнутом, если число неустойчивых корней l= 2.
Сформулированные выше правила определения (не) устойчивости замкнутой системы по ЛАФЧХ разомкнутой системы полностью применимы и для дискретных систем. Особенностью является лишь то, что ЛФЧХ дискретных систем строятся в функции псевдочастоты , а в случае формулировки устойчивости для неустойчивой в разомкнутом состоянии дискретной системы l означает число корней, по модулю больше единицы, т. е. находящихся вне круга единичного радиуса.
3.2. Анализ точности и качества процессов управления
3.2.1. Оценка точности САУ в установившихся режимах
3.2.1.1. Точность САУ в режиме стабилизации
Среди типовых режимов работы САУ простейшим, но и широко используемым в технике и технологии режимом является работа при постоянной величине управляющего воздействия или просто стабилизация. Основная задача системы стабилизации – поддержание регулируемой величины на заданном постоянном уровне в условиях существования возмущающих воздействий.
В этом параграфе мы оценим ошибки системы в режиме стабилизации, когда и управляющее и возмущающее воздействия имеют ступенчатую форму. В качестве объекта исследования примем одноконтурную систему с возмущающим воздействием f, приложенным в середине прямого канала системы (рис. 3.15).
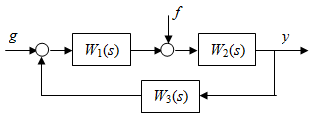
Рис. 3.15. Одноконтурная система с возмущающим воздействием
Рассмотрим три варианта состава звеньев в прямом канале системы:
1) все звенья являются позиционными;
2) в составе 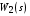 есть хотя бы одно интегрирующее звено; есть хотя бы одно интегрирующее звено;
3) в составе 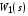 есть хотя бы одно интегрирующее звено. есть хотя бы одно интегрирующее звено.
Позиционными будем называть звенья безинерционные 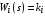 или динамические звенья 1-го и 2-го порядка, свободные члены передаточных функций которых равны единице. Например, или динамические звенья 1-го и 2-го порядка, свободные члены передаточных функций которых равны единице. Например,
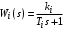 , , 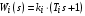 , , 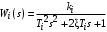 , ,
и их комбинации 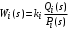 , ,
где Qi(s) и Pi(s) полиномы со свободными членами равными единице.
Первый вариант – все звенья прямого канала позиционные. Канал обратной связи во всех случаях будет приниматься позиционным. Тогда передаточная функция разомкнутой системы
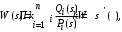
где 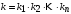 – общий коэффициент передачи разомкнутой системы; – общий коэффициент передачи разомкнутой системы;
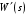 – рациональная дробь при – рациональная дробь при 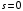 равная единице. равная единице.
Пусть на систему действует только управляющее воздействие 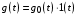 ступенчатой формы. Тогда установившееся значение ошибки от управляющего воздействия ступенчатой формы. Тогда установившееся значение ошибки от управляющего воздействия
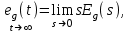
где 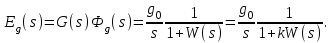
Окончательно
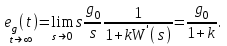
Таким образом, система, состоящая только из позиционных звеньев, отрабатывает ступенчатое управляющее воздействие с ошибкой, пропорциональной величине воздействия  и обратно пропорциональной (с точностью до единицы) общему коэффициенту передачи разомкнутой системы. и обратно пропорциональной (с точностью до единицы) общему коэффициенту передачи разомкнутой системы.
Пусть теперь на систему действует возмущение ступенчатой формы  . Установившееся значение ошибки от возмущения . Установившееся значение ошибки от возмущения
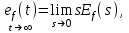
где 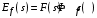 , , 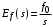 , ,
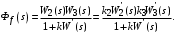
Подставляя в общую формулу, получим:
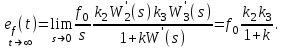
Таким образом, система, состоящая только из позиционных звеньев, имеет ошибки, определяемые как управляющим, так и возмущающим воздействием. Обе составляющие ошибки обратно пропорциональны (с точностью до единицы) общему коэффициенту передачи разомкнутой системы k.
Чем больше k, тем меньше ошибки. Увеличение k в рассматриваемой системе возможно только до определенного значения, называемого критическим, при котором система будет находиться на границе устойчивости (рис. 3.16).
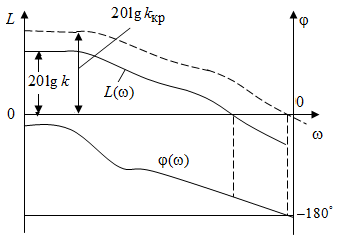
Рис. 3.16. Система на границе устойчивости
Второй вариант: в составе звеньев, описываемых передаточной функцией W2(s), есть интегрирующее звено
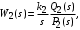
где 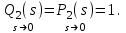
Передаточная функция разомкнутой системы
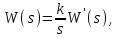
где 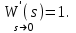
Передаточная функция замкнутой системы по ошибке от управляющего воздействия
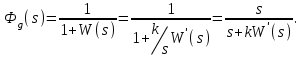
Передаточная функция замкнутой системы по ошибке от возмущающего воздействия
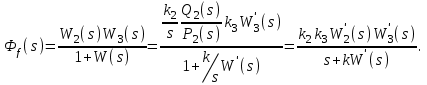
Ошибка установившегося режима по управляющему воздействию
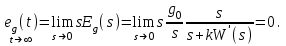
Ошибка установившегося режима по возмущающему воздействию
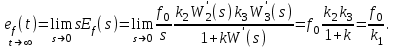
Таким образом, система, имеющая в прямом канале интегрирующее звено, расположенное после точки приложения возмущающего воздействия, обеспечивает отсутствие ошибки от ступенчатого управляющего воздействия и имеет постоянную ошибку, обусловленную ступенчатым возмущающим воздействием.
Третий вариант: интегрирующее звено включено в группу звеньев, описываемых передаточной функцией 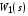 , т. е. , т. е. 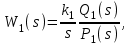 где где 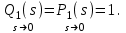
Тогда передаточная функция разомкнутой системы
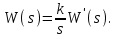
Передаточная функция замкнутой системы по ошибке от управляющего воздействия
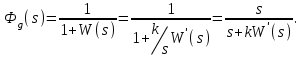
Передаточная функция замкнутой системы по ошибке от возмущающего воздействия
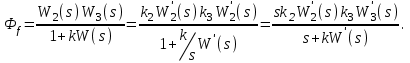
Ошибка установившегося режима по управляющему воздействию ступенчатой формы
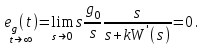
Ошибка установившегося режима по возмущающему воздействию ступенчатой формы
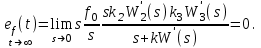
Таким образом, система, содержащая интегрирующее звено в прямом канале, расположенное до точки приложения возмущающего воздействия, не имеет ошибок как от управляющего, так и от возмущающего воздействий ступенчатой формы.
Система, имеющая интегрирующее звено в прямом канале, называется астатической системой 1-го порядка.
Астатическая система 1-го порядка воспроизводит ступенчатое управляющее воздействие без ошибки в установившемся режиме и полностью подавляет ступенчатое возмущающее воздействие, если оно действует в прямом канале после интегрирующего звена.
Вот почему интегральный или пропорционально-интегральные регуляторы ставятся всегда вначале прямого канала сразу после узла сравнения.
3.2.1.2. Установившиеся ошибки при отработке
медленно меняющихся внешних воздействий
Под медленно меняющимися внешними воздействиями будем понимать сигналы, описываемые степенными временными рядами
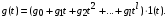
В эту группу воздействий входят почто все типовые воздействия, принятые в ТАУ для анализа и синтеза систем управления. В частности, первое слагаемое 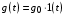 – ступенчатое воздействие; второе слагаемое – ступенчатое воздействие; второе слагаемое 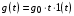 – скоростное (линейное) воздействие; третье слагаемое – скоростное (линейное) воздействие; третье слагаемое 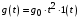 – параболическое (квадратичное) воздействие. – параболическое (квадратичное) воздействие.
Для установившейся ошибки воспроизведения медленно меняющихся воздействий было получено специальное выражение, имеющее для непрерывных систем следующую форму
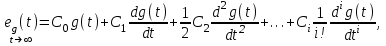
где 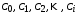 – коэффициенты ошибок, определяемые по выражению – коэффициенты ошибок, определяемые по выражению
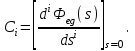
Так 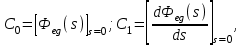 где где 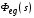 – передаточная функция замкнутой системы по ошибке от воздействия – передаточная функция замкнутой системы по ошибке от воздействия 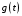 . На практике значения коэффициентов ошибок для . На практике значения коэффициентов ошибок для 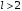 определяют по формулам, приведенным в справочнике. Для определяют по формулам, приведенным в справочнике. Для 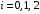 коэффициенты можно определять непосредственно по вышеприведенным формулам. коэффициенты можно определять непосредственно по вышеприведенным формулам.
Используя выражение для установившейся ошибки через коэффициенты ошибок, найдем значение коэффициентов ошибок при отработке непрерывной системой типовых воздействий: 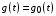 ; ; 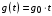 ; ; 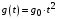 . .
1. Система статическая (порядок астатизма 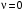 ), воздействие ступенчатое ), воздействие ступенчатое 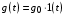 . .
Установившаяся ошибка при отработке ступенчатого воздействия
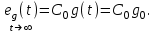
Заметим, что другие слагаемые выражения ошибки, содержащие производные от 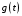 по времени будут равны нулю, так как по времени будут равны нулю, так как 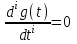 при при 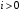 . .
Коэффициент ошибки
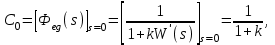
так как 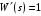 и значение установившейся ошибки и значение установившейся ошибки 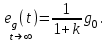
Отсюда следует, что:
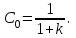
2. Система астатическая 1-го порядка (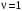 ). ).
Воздействие линейное 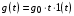 . .
Передаточная функция замкнутой системы по ошибке
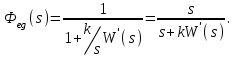
Установившаяся ошибка при отработке линейного воздействия
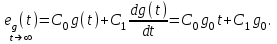
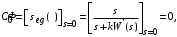
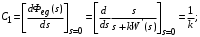
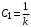 . .
Установившееся значение ошибки 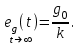 Ошибка при отработке линейного внешнего воздействия называется скоростной ошибкой. Она пропорциональна скорости изменения воздействия g0 и обратно пропорциональна общему коэффициенту усиления разомкнутой астатической системы 1-го порядка, который называется добротностью системы по скорости. Ошибка при отработке линейного внешнего воздействия называется скоростной ошибкой. Она пропорциональна скорости изменения воздействия g0 и обратно пропорциональна общему коэффициенту усиления разомкнутой астатической системы 1-го порядка, который называется добротностью системы по скорости.
3. Система астатическая 2-го порядка (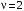 ). ).
Воздействие параболическое 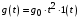 . .
Передаточная функция замкнутой системы по ошибке
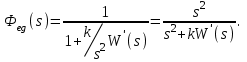
Установившаяся ошибка при отработке параболического воздействия:
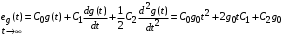 , ,
где коэффициенты ошибок равны:
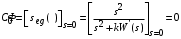 , ,
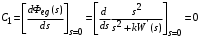 , ,
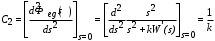 , ,
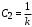 . .
Установившееся значение ошибки 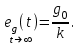
Ошибка при отработке параболического внешнего воздействия называ6ется ошибкой по ускорению. Она пропорциональна ускорению внешнего воздействия 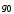 и обратно пропорциональна общему коэффициенту передачи разомкнутой астатической системы 2-го порядка, который называется добротностью системы по ускорению. и обратно пропорциональна общему коэффициенту передачи разомкнутой астатической системы 2-го порядка, который называется добротностью системы по ускорению.
3.2.1.3. Анализ влияния порядка астатизма
системы на установившиеся ошибки
при отработке типовых степенных воздействий
Обобщая приведенный анализ установившихся ошибок в системах различного порядка астатизма при отработке ступенчатых и медленно меняющихся воздействий, получим общие выражения установившихся ошибок в функции порядка астатизма и степени внешнего воздействия.
Пусть управляющее воздействие имеет форму 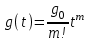 , и изображения по Лапласу , и изображения по Лапласу 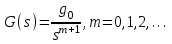
Изображение ошибки при таком воздействии будет
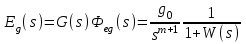 . .
Установившееся значение ошибки
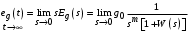 . .
Пусть передаточная функция разомкнутой системы имеет вид
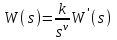 , ,
где k – общий коэффициент передачи системы; - порядок астатизма системы; 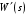 – передаточная функция, не содержащая нулевых полюсов. – передаточная функция, не содержащая нулевых полюсов.
Тогда установившееся значение ошибки
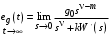 . .
Отсюда видно, что  только при только при 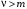 , т. е. порядок астатизма системы должен быть боше степени m воздействия. , т. е. порядок астатизма системы должен быть боше степени m воздействия.
При 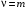 установившаяся ошибка имеет постоянную величину установившаяся ошибка имеет постоянную величину 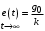 , что означает, что системы с астатизмом 1-го и 2-го порядка будут иметь постоянные ошибки при отработке линейного и квадратичного воздействий соответственно. , что означает, что системы с астатизмом 1-го и 2-го порядка будут иметь постоянные ошибки при отработке линейного и квадратичного воздействий соответственно.
При 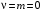 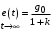 . Это ошибка системы с . Это ошибка системы с 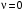 при отработке ступенчатого воздействия. при отработке ступенчатого воздействия.
И, наконец, при 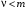 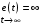 . Так система, не имеющая интеграторов, будет иметь бесконечную ошибку уже при воздействии . Так система, не имеющая интеграторов, будет иметь бесконечную ошибку уже при воздействии 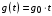 , т. е. при , т. е. при 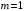 . .
В табл. 3.2 сведены установившиеся ошибки непрерывных систем различного порядка астатизма при отработке внешних воздействий степенной формы.
|
 Скачать 1.97 Mb.
Скачать 1.97 Mb. . Рассмотрим это соответствие.
. Рассмотрим это соответствие. 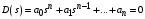 ,
,
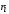
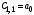
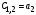
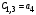
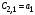
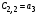
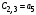
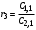
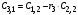
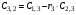
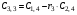
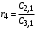
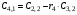
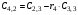
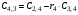
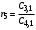
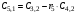
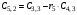
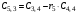
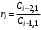
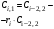
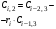
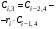
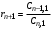
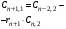
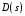 называется характеристическим полиномом. Его можно представить в соответствии с теоремой Безу следующим образом:
называется характеристическим полиномом. Его можно представить в соответствии с теоремой Безу следующим образом: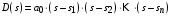
 де
де 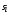 (
(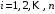 ) – корни характеристического уравнения
) – корни характеристического уравнения 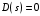 ;
; 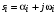 . На комплексной плоскости каждый корень может быть представлен вектором (рис. 3.2). Длина вектора
. На комплексной плоскости каждый корень может быть представлен вектором (рис. 3.2). Длина вектора 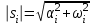 , угол поворота от положительной вещественной полуоси равен аргументу
, угол поворота от положительной вещественной полуоси равен аргументу 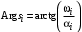 . Отдельные сомножители
. Отдельные сомножители  могут быть представлены векторами, проведенными из точек
могут быть представлены векторами, проведенными из точек  .
. , тогда вектор
, тогда вектор  будет скользить своим концом по мнимой оси при изменении частоты
будет скользить своим концом по мнимой оси при изменении частоты 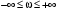 .
.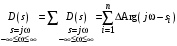 ,
,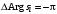 (рис. 3.3, б).
(рис. 3.3, б).
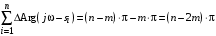 .
.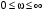 , то суммарное приращение аргумента
, то суммарное приращение аргумента 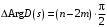 .
.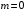 ), находим, что
), находим, что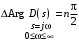 .
.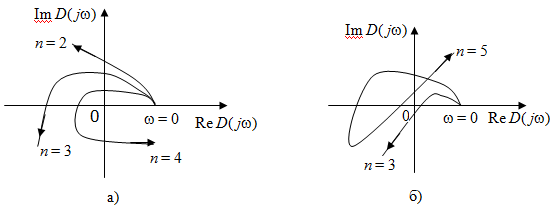
 проходит через начало координат.
проходит через начало координат.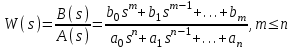 .
.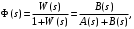
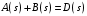 характеристический полином замкнутой системы.
характеристический полином замкнутой системы.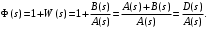
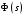 равен
равен 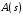 характеристический полином разомкнутой системы. Заметим также, что степени числителя и знаменателя равны, так как m n.
характеристический полином разомкнутой системы. Заметим также, что степени числителя и знаменателя равны, так как m n.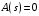 лежат в левой полуплоскости. Для того, чтобы и замкнутая система была устойчивой, необходимо, чтобы все корни
лежат в левой полуплоскости. Для того, чтобы и замкнутая система была устойчивой, необходимо, чтобы все корни 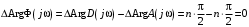 .
.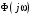 при
при 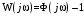 .
.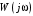 , но в координатах, где мнимая ось перенесена на (1) (рис. 3.5, б).
, но в координатах, где мнимая ось перенесена на (1) (рис. 3.5, б). 
 , штриховыми линиями показаны АФХ при уменьшении коэффициента усиления разомкнутых систем.
, штриховыми линиями показаны АФХ при уменьшении коэффициента усиления разомкнутых систем.
 ) применение критерия Найквиста имеет свою особенность. Дело в том, что АФХ таких систем в области низких, частот приближаются к одной из осей комплексной плоскости. Поэтому для определения устойчивости по критерию Найквиста необходимо предварительно дополнять АФХ дугами
) применение критерия Найквиста имеет свою особенность. Дело в том, что АФХ таких систем в области низких, частот приближаются к одной из осей комплексной плоскости. Поэтому для определения устойчивости по критерию Найквиста необходимо предварительно дополнять АФХ дугами 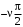 окружности бесконечно большого радиуса (рис. 3.7).
окружности бесконечно большого радиуса (рис. 3.7).
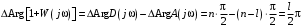 .
. сли разомкнутая система неустойчива, то для того, чтобы была устойчивой замкнутая система, необходимо и достаточно, чтобы АФХ разомкнутой системы охватывала критическую точку в положительном направлении
сли разомкнутая система неустойчива, то для того, чтобы была устойчивой замкнутая система, необходимо и достаточно, чтобы АФХ разомкнутой системы охватывала критическую точку в положительном направлении 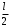 раз, где l – число корней характеристического уравнения разомкнутой системы в правой полуплоскости.
раз, где l – число корней характеристического уравнения разомкнутой системы в правой полуплоскости. сли разомкнутая система неустойчива, то для того, чтобы разность между числами положительных и отрицательных переходов АФХ разомкнутой системы через отрезок вещественной оси (, 1) была равна
сли разомкнутая система неустойчива, то для того, чтобы разность между числами положительных и отрицательных переходов АФХ разомкнутой системы через отрезок вещественной оси (, 1) была равна  ассмотрим теперь, как будет формироваться критерий Найквиста с использованием логарифмических амплитудно-частотных фазочастотных характеристик. Прежде всего установим, где будет расположена критическая точка с координатами
ассмотрим теперь, как будет формироваться критерий Найквиста с использованием логарифмических амплитудно-частотных фазочастотных характеристик. Прежде всего установим, где будет расположена критическая точка с координатами 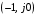 в плоскости АФХ разомкнутой системы. Отметим, что критической точке
в плоскости АФХ разомкнутой системы. Отметим, что критической точке 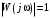 , а угол сдвига
, а угол сдвига 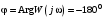 рис. 3.11.
рис. 3.11. 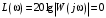 , т. е. график
, т. е. график 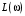 пересекает ось частот, и
пересекает ось частот, и 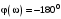 , т. е. график
, т. е. график 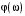 пересекает линию (180). Таким образом, если замкнутая система будет находиться на границе устойчивости, то ЛАЧХ и ЛФЧХ разомкнутой системы пересекают линии
пересекает линию (180). Таким образом, если замкнутая система будет находиться на границе устойчивости, то ЛАЧХ и ЛФЧХ разомкнутой системы пересекают линии 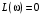 и
и 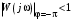 .
.
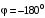 .
.
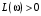 , т. е. до точки пересечения
, т. е. до точки пересечения 
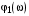 соответствует системе, устойчивой в разомкнутом состоянии и находящейся на границе устойчивости в замкнутом состоянии. Характеристика
соответствует системе, устойчивой в разомкнутом состоянии и находящейся на границе устойчивости в замкнутом состоянии. Характеристика 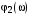 принадлежит системе устойчивой в разомкнутом и замкнутом состояниях. И, наконец,
принадлежит системе устойчивой в разомкнутом и замкнутом состояниях. И, наконец, 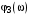 свидетельствует о неустойчивости в разомкнутом состоянии и устойчивости в замкнутом, если число неустойчивых корней l= 2.
свидетельствует о неустойчивости в разомкнутом состоянии и устойчивости в замкнутом, если число неустойчивых корней l= 2.
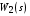 есть хотя бы одно интегрирующее звено;
есть хотя бы одно интегрирующее звено;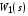 есть хотя бы одно интегрирующее звено.
есть хотя бы одно интегрирующее звено.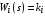 или динамические звенья 1-го и 2-го порядка, свободные члены передаточных функций которых равны единице. Например,
или динамические звенья 1-го и 2-го порядка, свободные члены передаточных функций которых равны единице. Например,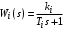 ,
, 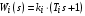 ,
, 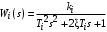 ,
,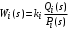 ,
, 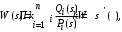
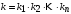 – общий коэффициент передачи разомкнутой системы;
– общий коэффициент передачи разомкнутой системы; 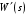 – рациональная дробь при
– рациональная дробь при 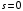 равная единице.
равная единице.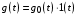 ступенчатой формы. Тогда установившееся значение ошибки от управляющего воздействия
ступенчатой формы. Тогда установившееся значение ошибки от управляющего воздействия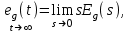
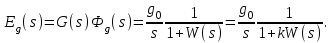
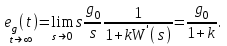
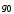 и обратно пропорциональной (с точностью до единицы) общему коэффициенту передачи разомкнутой системы.
и обратно пропорциональной (с точностью до единицы) общему коэффициенту передачи разомкнутой системы.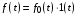 . Установившееся значение ошибки от возмущения
. Установившееся значение ошибки от возмущения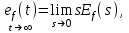
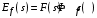 ,
, 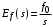 ,
,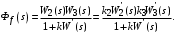
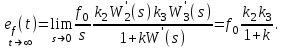

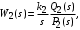
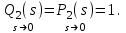
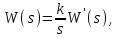
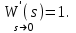
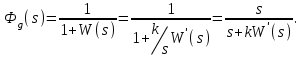
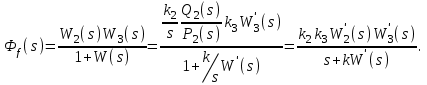
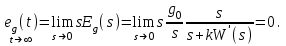
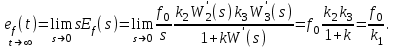
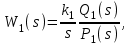 где
где 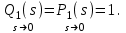
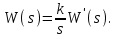
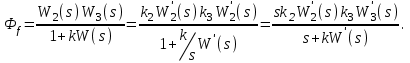
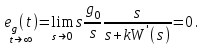
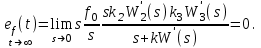
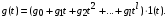
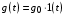 – ступенчатое воздействие; второе слагаемое
– ступенчатое воздействие; второе слагаемое 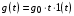 – скоростное (линейное) воздействие; третье слагаемое
– скоростное (линейное) воздействие; третье слагаемое 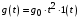 – параболическое (квадратичное) воздействие.
– параболическое (квадратичное) воздействие.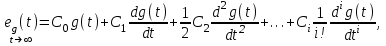
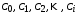 – коэффициенты ошибок, определяемые по выражению
– коэффициенты ошибок, определяемые по выражению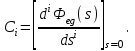
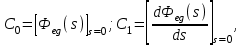 где
где 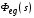 – передаточная функция замкнутой системы по ошибке от воздействия
– передаточная функция замкнутой системы по ошибке от воздействия 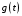 . На практике значения коэффициентов ошибок для
. На практике значения коэффициентов ошибок для 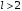 определяют по формулам, приведенным в справочнике. Для
определяют по формулам, приведенным в справочнике. Для 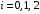 коэффициенты можно определять непосредственно по вышеприведенным формулам.
коэффициенты можно определять непосредственно по вышеприведенным формулам.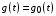 ;
; 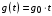 ;
; 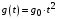 .
.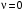 ), воздействие ступенчатое
), воздействие ступенчатое 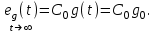
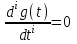 при
при 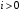 .
.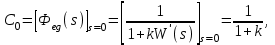
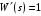 и значение установившейся ошибки
и значение установившейся ошибки 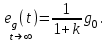
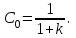
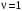 ).
).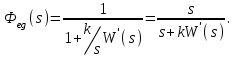
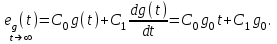
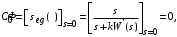
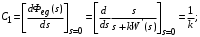
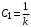 .
.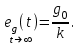 Ошибка при отработке линейного внешнего воздействия называется скоростной ошибкой. Она пропорциональна скорости изменения воздействия g0 и обратно пропорциональна общему коэффициенту усиления разомкнутой астатической системы 1-го порядка, который называется добротностью системы по скорости.
Ошибка при отработке линейного внешнего воздействия называется скоростной ошибкой. Она пропорциональна скорости изменения воздействия g0 и обратно пропорциональна общему коэффициенту усиления разомкнутой астатической системы 1-го порядка, который называется добротностью системы по скорости. ).
).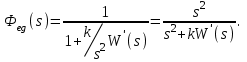
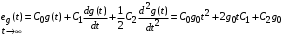 ,
,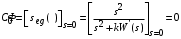 ,
,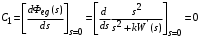 ,
,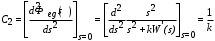 ,
,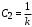 .
.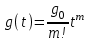 , и изображения по Лапласу
, и изображения по Лапласу 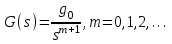
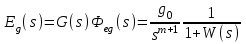 .
.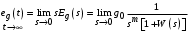 .
.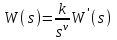 ,
,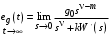 .
. только при
только при 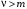 , т. е. порядок астатизма системы должен быть боше степени m воздействия.
, т. е. порядок астатизма системы должен быть боше степени m воздействия. 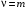 установившаяся ошибка имеет постоянную величину
установившаяся ошибка имеет постоянную величину 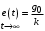 , что означает, что системы с астатизмом 1-го и 2-го порядка будут иметь постоянные ошибки при отработке линейного и квадратичного воздействий соответственно.
, что означает, что системы с астатизмом 1-го и 2-го порядка будут иметь постоянные ошибки при отработке линейного и квадратичного воздействий соответственно.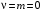
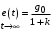 . Это ошибка системы с
. Это ошибка системы с 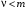
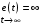 . Так система, не имеющая интеграторов, будет иметь бесконечную ошибку уже при воздействии
. Так система, не имеющая интеграторов, будет иметь бесконечную ошибку уже при воздействии 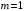 .
.