Учебное пособие санктпетербург 2016 удк 681. 5 (075. 8) Ббк 22. 161я73 к 59 Рецензенты
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
Приравнивая |
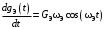 ; ; 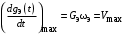 . . | (4.1) |
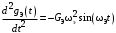 ; ; 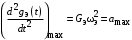 | (4.2) |
Разделив (4.2) на (4.1) и получим
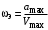 . . | (4.3) |
Подставим (4.3) в (4.1) и получим
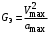 . . | (4.4) |
Определив параметры эквивалентного воздействия, находим максимальную ошибку
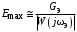 .
.Приравняв максимальную и допустимую ошибки
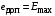 , получим:
, получим: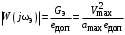 .
.З
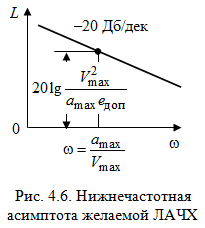 начит нижнечастотная асимптота желаемой ЛАЧХ (рис. 4.6) должна пройти через контрольную точку с координатами:
начит нижнечастотная асимптота желаемой ЛАЧХ (рис. 4.6) должна пройти через контрольную точку с координатами: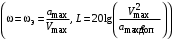
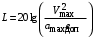 .
.Если в контрольной точке асимптоту претерпевает излом с наклона (20 дБ/дек) на наклон (40 дБ/дек), то ордината контрольной точки рассчитывается по формуле:
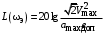 ,
,где
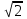 учитывает отличие действительной ЛАЧХ от асимптотической.
учитывает отличие действительной ЛАЧХ от асимптотической.4.2.2. Синтез желаемой ЛАЧХ в области средних частот
Как отмечалось выше, желаемая ЛАЧХ в области средних частот должна иметь наклон (20 дБ/дек). Поэтому задачей синтеза желаемой ЛАЧХ в области средних частот является определение местоположения участка с наклоном (20 дБ/дек), задаваемое, например, с помощью частоты среза
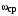 и его протяженность.
и его протяженность.Существует три метода определения
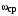 и протяженности участка с наклоном (20 дБ/дек): метод В.В. Солодовникова, метод В.А. Бесекерского и метод А.А. Вавилова.
и протяженности участка с наклоном (20 дБ/дек): метод В.В. Солодовникова, метод В.А. Бесекерского и метод А.А. Вавилова.В методе В.В. Солодовникова частота среза
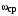 определяется по номограмме Солодовникова (рис. 4.7), для которой входными данными являются:
определяется по номограмме Солодовникова (рис. 4.7), для которой входными данными являются: 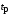 – время регулирования (до входа в зону 5 %
– время регулирования (до входа в зону 5 % 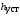 ) и
) и 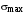 , % – максимальное перерегулирование переходной характеристики. Из номограммы определяется частота среза
, % – максимальное перерегулирование переходной характеристики. Из номограммы определяется частота среза 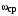 и значение
и значение 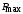 типовой вещественной характеристики замкнутой системы (рис. 4.8).
типовой вещественной характеристики замкнутой системы (рис. 4.8).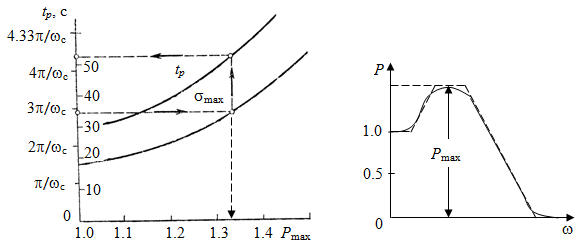
Рис. 4.7. Номограмма Рис. 4.8. Типовая вещественная
В.В. Солодовникова характеристика замкнутой системы
Из рис. 4.7 видно (штриховыми стрелками), что для заданных
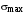 = 34% и времени регулирования
= 34% и времени регулирования 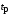 = 0.5 с значения
= 0.5 с значения 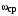 и
и 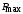 равны соответственно:
равны соответственно: 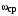 = 4.33/0.5 = 27.26 c1 , значение
= 4.33/0.5 = 27.26 c1 , значение 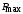 = 1.33.
= 1.33. Протяженность участка с наклоном (20 дБ/дек) определяется значением
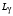 (рис. 4.9), котороенаходится из графика
(рис. 4.9), котороенаходится из графика 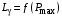 (рис. 4.10) по найденному выше значению
(рис. 4.10) по найденному выше значению 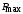 .
.Так для найденного из примера Pmax = 1.33 по графику (4.10) находим
L = 12.5 дБ.
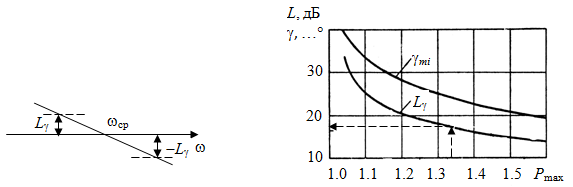
Рис. 4.9. Определение участка Рис. 4.10. График
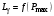
ЛАЧХ с наклоном (–20 дБ/дек) для определения значения
В методе Бесекерского по принятой величине показателя колебательности М рассчитываются значения частот, ограничивающих среднечастотный участок желаемой ЛАЧХ и задающих его местоположение (рис. 4.11).
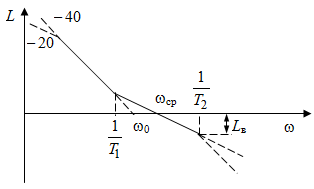
Рис. 4.11. Построение желаемой ЛАЧХ по методу Бессекерского
Слева от частоты среза участок ЛАЧХ с наклоном (20 дБ/дек) ограничивается точкой пересечения с низкочастотной асимптотой, имеющей наклон (40 дБ/дек) на частоте
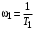 , где
, где 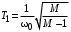 .
.Справа от частоты среза, среднечастотный участок ограничивается частотой
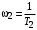 , где
, где 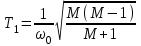 .
.После частоты
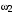 наклон желаемой ЛАЧХ может быть любым, но не положительным. Ограничением наклона в области высоких частот служит нулевой, при котором ЛАЧХ будет проходить параллельно оси частот на расстоянии
наклон желаемой ЛАЧХ может быть любым, но не положительным. Ограничением наклона в области высоких частот служит нулевой, при котором ЛАЧХ будет проходить параллельно оси частот на расстоянии  .
.Наконец, метод А.А. Вавилова предлагает использовать для построения среднечастотного участка желаемой ЛАЧХ специальные номограммы синтеза по критерию максимального быстродействия при заданном значении максимальной динамической ошибки (рис. 4.12, а и б). Метод используется для синтеза сложных систем с высоким порядком астатизма и оптимизирует переходные процессы по ошибке при степенных воздействиях.
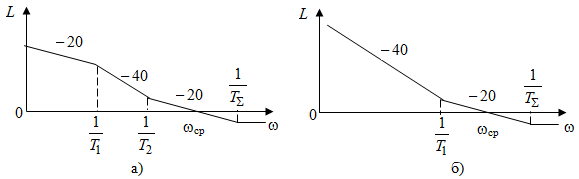
Рис. 4.12. Варианты построения желаемой ЛАЧХ методом А.А. Вавилова
Желаемая ЛАЧХ непрерывных систем в области низких частот
 совпадают с желаемыми ЛАЧХ (наклон ЛАЧХ и коэффициент передачи на контрольной частоте) определяется исходя из требований к точности в установившемся режиме.
совпадают с желаемыми ЛАЧХ (наклон ЛАЧХ и коэффициент передачи на контрольной частоте) определяется исходя из требований к точности в установившемся режиме.В области средних частот желаемые ЛАЧХ имеют наклон
(20 дБ/дек). Параметры ЛАЧХ в этой области определяют запас устойчивости, системы, вид и время затухания переходного процесса. Частота среза
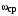 и протяженность участка с наклоном (20 дБ/дек) определяются или по заданным
и протяженность участка с наклоном (20 дБ/дек) определяются или по заданным 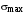 и
и 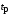 или по заданному показателю колебательности М. Заданный показатель будет достигаться, если выполняются условия:
или по заданному показателю колебательности М. Заданный показатель будет достигаться, если выполняются условия: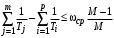 при
при 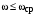 ;
;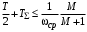 при
при 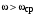 .
.4.3. Синтез корректирующих устройств
4.3.1. Схемы включения и классификация
корректирующих устройств
Корректирующим устройством, в общем случае, называется дополнительная часть системы, вводимая для улучшения ее динамических свойств.
Существует три способа включения корректирующих устройств в основную систему:
- последовательно в прямой канал передачи (рис. 4.13, а);
- в виде положительной или обратной связи, охватывающей часть элементов прямого канала (рис. 4.13, б);
- в виде параллельной прямой связи, включаемой параллельно участку прямого канала (рис. 4.13, в).
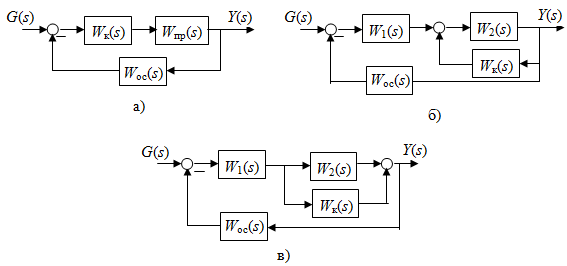
Рис. 4.13. Способы включения корректирующих устройств: а) последовательно
в прямой канал передачи; б) в виде положительной или обратной связи;
в) в виде параллельной прямой связи
В соответствии со способом включения корректирующего устройства называются последовательными, параллельными обратными и параллельными прямыми.
В соответствии с физической природой сигналов в системе управления корректирующие устройства могут быть механическими, гидравлическими, пневматическими, электрическими, электронными и, как разновидность электронных, программными, реализованными на интегральных схемах или микроконтроллерах.
Наконец, корректирующие устройства могут быть пассивными и активными в зависимости от того, использует ли корректирующее устройство энергию внешнего источника или не использует. Примерами пассивных корректирующих устройств являются электрические четырехполюсники, компонентами которых служат резисторы и конденсаторы. Примером активных корректирующих устройств являются операционные усилители и программно реализуемые корректирующие алгоритмы.
4.3.2. Определение передаточной функции
последовательного корректирующего звена
Если известны передаточные функции cкорректированной разомкнутой системы (Wск(s)) и некорректированной системы (Wнк(s)), то передаточная функция корректирующего устройства определяется просто как
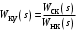 .
.Если желаемая передаточная функция неизвестна, и синтез корректирующего устройства выполняется совместно с синтезом желаемой ЛАЧХ, то определить ЛАЧХ корректирующего устройства можно графически (рис. 4.14), соблюдая условие получения наиболее простой реализуемой характеристики и передаточной функции корректирующего устройства:
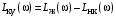 .
.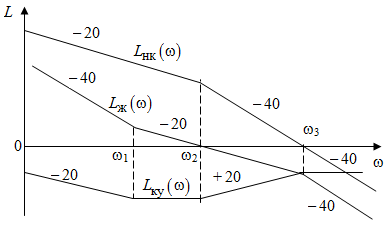
Рис. 4.14. Графическое определение желаемой ЛАЧХ корректирующего устройства
Согласно найденной ЛАЧХ корректирующего устройства
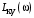 на рис. 4.14, передаточная функция запишется в виде:
на рис. 4.14, передаточная функция запишется в виде: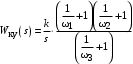 ,
,где kопределяется по
 на частоте = 1с1.
на частоте = 1с1.4.3.3. Определение передаточной функции
корректирующего устройства в виде отрицательной
местной обратной связи
Часто корректирующие устройства, включаемые в цепь обратной связи части некорректируемой системы, называют параллельными, подчеркивая их отличие от последовательных корректирующих устройств.
Параллельными корректирующими звеньями охватывают, как правило, звенья исходной системы, имеющие большие коэффициенты усиления и частично нелинейные характеристики. Включение параллельного корректирующего устройства сглаживает нелинейность характеристик и повышает степень стабильности контура.
О
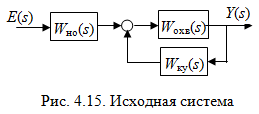 бозначим через
бозначим через 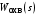 передаточную функцию звеньев, охваченных местной обратной связью и через
передаточную функцию звеньев, охваченных местной обратной связью и через 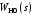 передаточную функцию остальных звеньев системы (рис. 4.15).
передаточную функцию остальных звеньев системы (рис. 4.15).Тогда передаточная функция разомкнутого контура
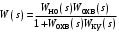
Принимая равенство
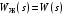 , получим:
, получим: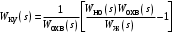 .
.Если принять во внимание свойство звеньев, охваченных местной обратной связью, т. е.
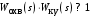 ,
,что практически выполняется, то передаточная функция корректирующего устройства может быть принята равной
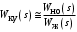 .
.Если формирование
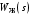 выполняется графически с помощью желаемой ЛАЧХ, то определение передаточной функции корректирующего устройства проще выполнить также графически через ЛАЧХ (рис. 4.14):
выполняется графически с помощью желаемой ЛАЧХ, то определение передаточной функции корректирующего устройства проще выполнить также графически через ЛАЧХ (рис. 4.14):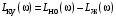 .
.В соответствии с характеристикой
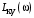 , полученной на рис. 4.15 графически, передаточная функция запишется в виде:
, полученной на рис. 4.15 графически, передаточная функция запишется в виде: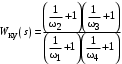 .
.
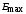 и
и 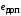 , имеем
, имеем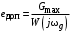 ,
, ткуда
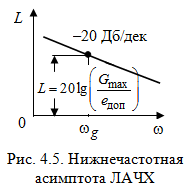
ткуда 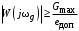 . Тогда нижнечастотная асимптота ЛАЧХ (рис.4.5) это прямая линия с наклоном (20 дБ/дек), проходящая через точку с координатами:
. Тогда нижнечастотная асимптота ЛАЧХ (рис.4.5) это прямая линия с наклоном (20 дБ/дек), проходящая через точку с координатами: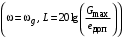 .
.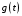 произвольной формы.
произвольной формы.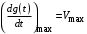 и максимальное ускорение
и максимальное ускорение 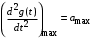 .
.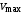 и
и 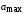 соответственно:
соответственно: 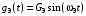 .
.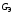 и
и 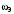 находим
находим 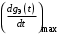 и
и 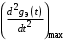 и приравниваем их
и приравниваем их