Учебное пособие санктпетербург 2016 удк 681. 5 (075. 8) Ббк 22. 161я73 к 59 Рецензенты
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
2.1.1. Дифференциальные и разностные уравнения Уравнения состояния САУ Пространство состояний САУ это бесконечная совокупность временных моментов состояния системы, описанная конечной совокупностью переменных состояния. Число переменных состояния обычно принимается равным порядку общего дифференцированного уравнения системы, т.е. числу дифференцированных уравнений 1-го порядка. Уравнения состояния записываются обычно в нормальной форме Коши и имеют вид: 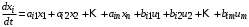 , , 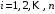 . .В левой части уравнения состояния всегда производная переменной состояния, а в правой части сумма всех переменных состояния и внешних воздействий со своими коэффициентами. Полное описание в пространстве состояния будет представлять систему из  дифференцированных уравнений 1-го порядка в форме Коши. дифференцированных уравнений 1-го порядка в форме Коши.Дифференциально-разностные уравнения САУ Дифференциальные (в частных случаях, алгебраические) уравнения непрерывных систем являются основной первичной формы математического описания любой САУ. Они могут использоваться самостоятельно для выполнения задач анализа и синтеза или служить основой для создания других форм математического описания. Дифференциальные и алгебраические уравнения непрерывных САУ составляются на основании изучения и осознания основных физических, химических и информационных процессов, происходящих в объекте управления и системе в целом. Часто для записи уравнений используются уже известные законы, устанавливающие связь между технологическими переменными величинами. Преобразование Лапласа Несмотря на неограниченные возможности компьютерных технологий по решению систем дифференциальных и разностных уравнений преобразование Лапласа остается по-прежнему широко используемым при решении задач анализа и синтеза САУ. Непрерывным преобразованием Лапласа непрерывной временной функции f(t) называется следующее преобразование 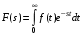 , ,где s = + j, и - постоянные, j = 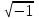 . Преобразуемая функция f(t) часто называется оригиналом, а F(s) – изображением функции f(t). К функции f(t) предъявляется требование, чтобы она была однозначной и удовлетворяла условию f(t) = 0 при t < 0. . Преобразуемая функция f(t) часто называется оригиналом, а F(s) – изображением функции f(t). К функции f(t) предъявляется требование, чтобы она была однозначной и удовлетворяла условию f(t) = 0 при t < 0.Приведем в качестве примеров непрерывного преобразования изображения единичной ступенчатой функции f(t) = 1(t). 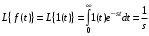 . .Основные свойства преобразования Лапласа Свойство линейности Непрерывное преобразование Лапласа являются линейным, т. е. изображение линейной комбинации функций равно линейной комбинации их изображений. Так если 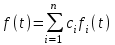 , то , то 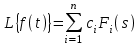 . .Изображение смещенной функции (теорема сдвига) Сдвигу функции оригинала на , т. е. 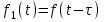 соответствует умножение непрерывного изображения на соответствует умножение непрерывного изображения на 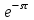 : :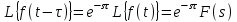 . .Изображение производной (конечной разности) n -порядка Если 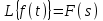 , то , то 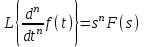 , при f(0) = 0 и всех , при f(0) = 0 и всех 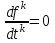 , k = 1, 2, …, n–1. Другими словами взятию производной n-го порядка соответствует при нулевых начальных условиях умножение изображения на sn. , k = 1, 2, …, n–1. Другими словами взятию производной n-го порядка соответствует при нулевых начальных условиях умножение изображения на sn.4. Изображение интеграла (конечной суммы) функции-оригинала Свойства изменения изображений функции после ее интегрирования или взятия конечной суммы в дискретном варианте является “обратными” по отношению к свойствам дифференцирования или взятия конечных разностей: 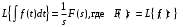 Резюмируя свойства 3 и 4 отметим, что s – оператор дифференцирования в непрерывной области; 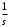 – оператор интегрирования в непрерывной области. – оператор интегрирования в непрерывной области.5. Свойство изображения свертываемых функций (теорема свертки) Сверткой двух непрерывных называется функция, значения которой вычисляются согласно 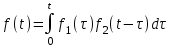 для непрерывного времени. для непрерывного времени.Формулировка свойства об изображении свертки для непрерывного времени: - изображение свертки равно произведению изображений свертываемых функций. Если 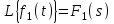 и и 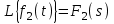 , то , то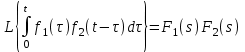 . .Определение начального значения функции оригинала по известному изображению Зная изображение F(s) можно сравнительно просто вычислить начальное и конечное значения функции-оригинала. Начальное значение непрерывной функции 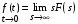 . .7. Конечное значение функции-оригинала В непрерывном времени 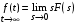 . .Преобразование дифференциальных и разностных уравнений. Пусть непрерывная система описывается уравнением 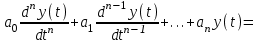 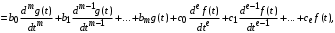 где y(t), g(t), f(t) – выходная управляемая величина, управляющее и возмущающее воздействие соответственно; a0, …, an; b0, …, bm; c0, …, ce – постоянные коэффициенты. Предположим, что система работает при нулевых начальных условиях, т. е. при t = 0 имеем 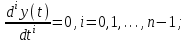 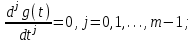 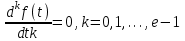 . Подвергнем заданное дифференциальное уравнение преобразованию Лапласа, используя свойства линейности и изображения производной, . Подвергнем заданное дифференциальное уравнение преобразованию Лапласа, используя свойства линейности и изображения производной,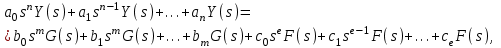 где Y(s), G(s),F(s) – изображения по Лапласу функций y(t), g(t), f(t). Запишем полученное уравнение в более сжатой форме 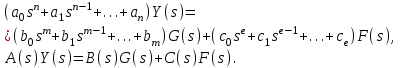 Сравнивая полученное уравнение с исходным, приходим к правилу преобразования по Лапласу любого дифференциального уравнения. Чтобы получить преобразованное по Лапласу уравнение, необходимо операторы дифференцирования 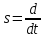 заменить комплексными операторами s = + j, а все временные функции заменить их изображением. заменить комплексными операторами s = + j, а все временные функции заменить их изображением.Отметим, что преобразование по Лапласу уравнение является алгебраическим, что в корне облегчает все математические операции при его использовании. Теперь возьмем отношения изображений присутствующих в уравнении величин, принимая одну из них (управление G(s) или возмущение F(s)) равной нулю: 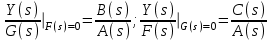 . .Полученные отношения представляют собой передаточные функции системы по управляющему и возмущающему воздействиям: 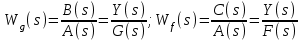 . .Передаточной функцией системы (элемента системы) называется отношение изображений по Лапласу выходной и входной величин при нулевых начальных условиях. Понятие передаточной функции является одним из фундаментальных в теории автоматического управления и широко используется на различных стадиях анализа и синтеза систем управления. 2.1.2. Векторно-матричное описание непрерывной системы Обобщая записанную в примере систему уравнений состояния, запишем ее для системы порядка  . .
Эту систему можно записать в векторно-матричной форме:
где А – матрица коэффициентов системы размерностью (nx n), называемая матрицей системы или матрицей состояния; X – действительный n-мерный вектор-столбец, компоненты которого переменные состояния; B – матрица коэффициентов системы при внешних воздействиях и поэтому называемая матрицей входа размерностью (n x m); U– действительный m-мерный вектор-столбец, содержащий в качестве своих элементов входные внешние воздействия (управляющие и возмущающие), называемый вектором входа. Значения этих матриц легко можно записать из системы уравнений (2.1): 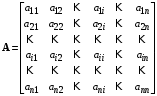 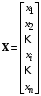 ; ;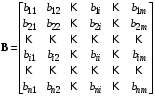 ; ; 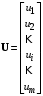 . .Если матрицы А и В постоянные, то система называется стационарной; если матрицы А и В – функции времени, то система называется нестационарной или системой с переменными коэффициентами. Основное матричное уравнение (2.2) обычно дополняется уравнением для вектора выходных переменных:
где C – матрица выхода системы, размерность которой зависит от размерности векторов X и Y; в одномерной системе, где y есть скалярная переменная, матрица С есть строка размерностью n; D – матрица связи с внешними воздействиями, ее размерность определяется размерностью векторов U и Y. Преобразование Лапласа матричного уравнения Запишем основное матричное уравнение системы:
Рассмотрим сначала однородное матричное уравнение системы при U(t) = 0. Тогда уравнение (2.4) запишется в виде: 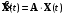 . .Выполнив преобразование Лапласа с учетом начальных условий, т.е. наличия вектора X(0), получим 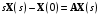 . .Объединяя члены, содержащие изображение вектора X(s), получим 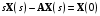 или или 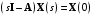 , откуда , откуда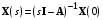 , ,где I– единичная матрица; матрица 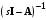 называется резольвентой матрицы А, которую можно записать следующим образом: называется резольвентой матрицы А, которую можно записать следующим образом: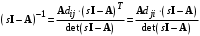 , ,где 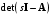 – определитель матрицы – определитель матрицы 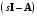 ; ; 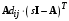 – квадратная матрица, элементами которой являются алгебраические дополнения элементов – квадратная матрица, элементами которой являются алгебраические дополнения элементов 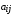 матрицы матрицы 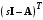 ; ; 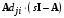 – матрица, элементами которой являются алгебраические дополнения элементов – матрица, элементами которой являются алгебраические дополнения элементов 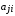 матрицы матрицы 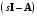 . . Матрица 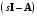 называется характеристической. называется характеристической. Ее определитель 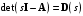 называется характеристическим полиномом. называется характеристическим полиномом. Уравнение 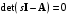 называется характеристическим уравнением. называется характеристическим уравнением. Рассмотрим неоднородное матричное уравнение системы: 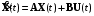 , , 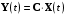 . .Выполнив преобразование Лапласа, принимая начальные условия 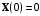 , получим: , получим: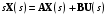 , , 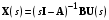 , ,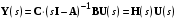 , ,где 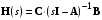 называется матричной передаточной функцией системы, которая вычисляется следующим образом: называется матричной передаточной функцией системы, которая вычисляется следующим образом: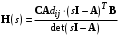 . .Заметим, что знаменатель H(s) это характеристический полином D(s) и корни характеристического уравнения D(s) = 0 являются одновременно полюсами передаточной функции системы H(s). Пример: Пусть уравнения состояния непрерывной части системы имеют вид: 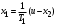 , , 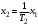 . .Тогда матрицы системы, входа и выхода запишется в виде соответственно: 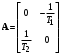 ; ; 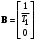 ; ; 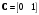 . .Определяем переходную матрицу 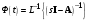 . .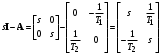 ; ; 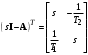 ; ;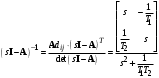 . .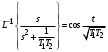 ; ; 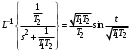 ; ;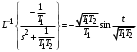 . .2.1.3. Временные характеристики систем и их элементов Временными характеристиками систем управления или их элементов называются реакции систем или элементов на входные сигналы, описываемые типовыми временными функциями. Их можно получить двумя способами: 1) экспериментальным, когда регистрируется выходная величина системы или элемента при подаче на их вход того или иного типового внешнего воздействия; 2) аналитическим, когда в правую часть дифференциального уравнения системы или элемента подставляется математическое выражение входного воздействия и решают уравнения при нулевых начальных условиях, т.е. получают аналитическое выражение временной характеристики, которое затем представляют в виде графика. Временные характеристики играют важную роль при решении задач анализа и синтеза систем управления, поэтому знание их совершенно необходимо как при проектировании, так и при эксплуатации систем управления. Различают две важнейшие временные характеристики систем управления или их элементов импульсная переходная характеристика (ИПХ) или функция веса; переходная характеристика (ПХ). 2.1.3.1. Импульсные переходные характеристики Импульсной переходной характеристикой (ИПХ) непрерывной системы называется реакция системы на импульсный сигнал, описываемый единичной 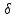 - функцией, при нулевых начальных условиях. - функцией, при нулевых начальных условиях.Определение единичной 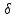 - функции: - функции: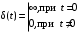 и и 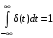 . .Изображение по Лапласу 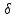 -функции: -функции: 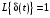 . Изображение . Изображение 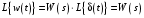 , поэтому ИПХ может быть найдена как , поэтому ИПХ может быть найдена как 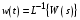 . . С помощью ИПХ может быть определена выходная величина системы при произвольном входном воздействием: 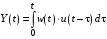 . . |

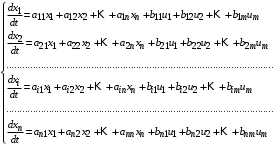 .
.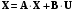 ,
,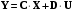 ,
,