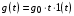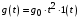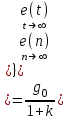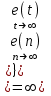Учебное пособие санктпетербург 2016 удк 681. 5 (075. 8) Ббк 22. 161я73 к 59 Рецензенты
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
Таблица 3.2
Таким образом, 1) Система с астатизмом 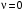 (статическая система) не способна воспроизводить линейные и квадратичные сигналы и поэтому не используются как следящая или программного управления; (статическая система) не способна воспроизводить линейные и квадратичные сигналы и поэтому не используются как следящая или программного управления;2) Система с астатизмом 1-го порядка ( 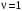 ) способна работать как СПУ; ) способна работать как СПУ;3) Система с астатизмом 2-го порядка ( 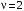 ) обеспечивает точное воспроизведение ступенчатых и линейных сигналов и может отрабатывать квадратичные воздействия с постоянной ошибкой; может работать в режиме слежения. ) обеспечивает точное воспроизведение ступенчатых и линейных сигналов и может отрабатывать квадратичные воздействия с постоянной ошибкой; может работать в режиме слежения.Значение установившейся ошибки от возмущающего воздействия степенной формы зависит не только от соотношения порядка астатизма системы и степени воздействия, но и от распределения интегрирующих звеньев между регулятором и объектом управления, т. е. зависит от точки приложения возмущающего воздействия в системе. Пусть регулятор содержит 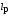 , а объект управления , а объект управления 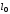 интеграторов. Тогда порядок астатизма системы интеграторов. Тогда порядок астатизма системы 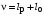 . .ПФ замкнутой системы по ошибке от возмущающего воздействия (рис. 3.15) 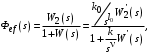 где 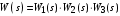 ; ; 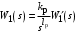 , , 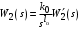 , , 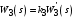 ; ; 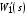 , , 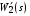 , , 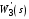 – передаточные функции, не имеющие нулевых полюсов. – передаточные функции, не имеющие нулевых полюсов.Тогда 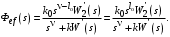 Установившееся значение ошибки от возмущающего воздействия степенной формы 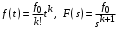 . .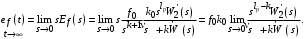 Из полученного выражения следует, что: 1. установившееся значение ошибки от возмущающего воздействия определяется соотношением числа интеграторов в регуляторе и степени воздействия и не зависит от числа интеграторов объекта управления; 2. отсутствие интеграторов в регуляторе вызывает ошибку: 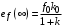 при при 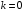 , , 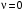 ; ;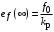 при при 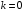 , , 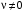 ; ;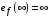 при при 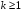 . .3. наличие интеграторов в регуляторе вызывает ошибку: 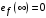 при при 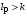 ; ;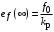 при при 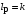 ; ;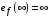 при при 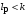 . .Таким образом, размещения интеграторов в регуляторе до точки приложения возмущения позволяет свести к нулю ошибки установившегося режима, выбирая число интеграторов больше степени возмущающего воздействия. 3.2.2. Оценка показателей качества работы САУ Для оценки качества переходных процессов в системах автоматического управления используются различные показатели, которые могут быть подразделены на четыре группы: 1) показатели переходной характеристики замкнутой системы; 2) частотные показатели качества; 3) корневые показатели; 4) интегральные оценки качества переходных процессов. 3.2.2.1. Показатели качества по переходной характеристике 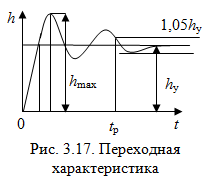 Показатели переходной характеристики непосредственно связаны с требованиями автоматизируемых процессов и поэтому называются прямыми показателями качества. К ним относятся (рис. 3.17): максимальное значение переходной характеристики hmax, время достижения максимального значения tmax, перерегулирование Показатели переходной характеристики непосредственно связаны с требованиями автоматизируемых процессов и поэтому называются прямыми показателями качества. К ним относятся (рис. 3.17): максимальное значение переходной характеристики hmax, время достижения максимального значения tmax, перерегулирование 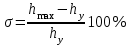 ; установившееся значение; время первого согласования (время подъема) ; установившееся значение; время первого согласования (время подъема) 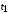 ; время регулирования ; время регулирования 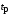 – время от начала переходной характеристики до момента ее входа в зону – время от начала переходной характеристики до момента ее входа в зону 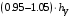 , после которого она остается в этой зоне. Величина зоны может быть иной, например 0.01hу, но в этом случае ее величина специально оговаривается. , после которого она остается в этой зоне. Величина зоны может быть иной, например 0.01hу, но в этом случае ее величина специально оговаривается.Такие же показатели определяются по переходной характеристике дискретно непрерывной или дискретной САУ. Разница состоит лишь в том, определение происходит по дискретным значениям переходной характеристики. При достаточно малом периоде квантования свойства дискретно непрерывной системы близки к свойствам непрерывной системы, поэтому дискретные значения переходной характеристики с большой долей уверенности могут быть соединены в плавную кривую. В ряде случаев получение переходной характеристики экспериментальным путем затруднительно как для непрерывной, так и для дискретной системы. Поэтому вместо прямых показателей качества используют косвенные показатели качества переходных процессов: частотные и корневые. Частотные показатели качества могут быть получены как экспериментальным, так и теоретическим путем. Они подразделяются на две группы: 1 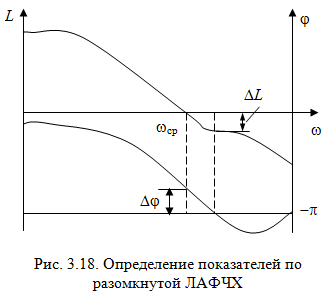 ) показатели, определяемые по ЛАФЧХ разомкнутой системы (рис. 3.18): частота среза ср, запас устойчивости по фазе и запас устойчивости по модулю L; наиболее информативны первые два показателя: частота среза с служит оценкой быстродействия замкнутой системы, запас по фазе тесно связан со степенью колебательности переходной характеристики; ) показатели, определяемые по ЛАФЧХ разомкнутой системы (рис. 3.18): частота среза ср, запас устойчивости по фазе и запас устойчивости по модулю L; наиболее информативны первые два показателя: частота среза с служит оценкой быстродействия замкнутой системы, запас по фазе тесно связан со степенью колебательности переходной характеристики;2) показатели, определяемые по амплитудно-частотной характеристике замкнутой системы (рис. 3.19). П 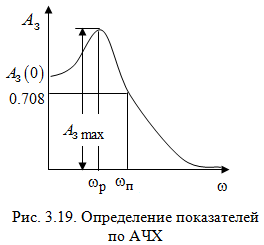 оказатель колебательности оказатель колебательности 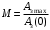 связан также со степенью колебательности замкнутой системы. Считаются удовлетворительными значения показателя колебательности в пределах связан также со степенью колебательности замкнутой системы. Считаются удовлетворительными значения показателя колебательности в пределах 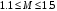 . .Резонансная частота системы 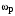 характеризует частоту колебаний, пропускаемую системой с наибольшим усилением. характеризует частоту колебаний, пропускаемую системой с наибольшим усилением.Полоса пропускания 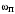 – частота, на которой – частота, на которой 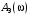 снижается на 3 дБ от начального значения снижается на 3 дБ от начального значения 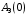 . . 3.2.2.2. Показатели качества по корневой плоскости К 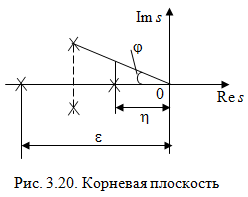 орневые оценки качества переходных процессов замкнутой непрерывной системы включает в себя следующие показатели (рис. 3.20): орневые оценки качества переходных процессов замкнутой непрерывной системы включает в себя следующие показатели (рис. 3.20): 1) показатель быстродействия (степень устойчивости) – определяется как расстояние от мнимой оси до ближайших вещественного или пары сопряженных комплексных корней; 2) колебательность 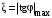 определяется как максимальный угол наклона к вещественной оси луча, проведенного из начала координат к одному из пары сопряженных комплексных корней; увеличение прямо пропорционально связано с перерегулированием и числом колебаний за время регулирования определяется как максимальный угол наклона к вещественной оси луча, проведенного из начала координат к одному из пары сопряженных комплексных корней; увеличение прямо пропорционально связано с перерегулированием и числом колебаний за время регулирования 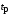 ; ;3) показатель затухания является характеристикой степени затухания переходных процессов и определяется как расстояние от мнимой оси до самых дальних вещественного или пары сопряженных комплексных корней. 3.2.2.3. Интегральные показатели качества Интегральные оценки качества широко используются для анализа и синтеза непрерывных систем. Различают простую интегральную и улучшенную интегральную оценки. Простая оценка (ИКО) определяется как 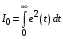 , ,где 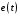 – ошибка переходного процесса. Улучшенные оценки определяются следующим образом: – ошибка переходного процесса. Улучшенные оценки определяются следующим образом: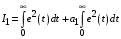 . .Чаще используются улучшенные оценки, так как минимуму простой ИКО соответствует слабо затухающий переходный процесс. 3.2.2.4. Связь частотных показателей с основными прямыми показателями качества Установить связь между частотными показателями (рис. 3.18) 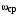 , , 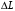 , , 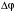 , M, , M, 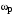 и прямыми показателями качества по переходной характеристике (рис. 3.17) и прямыми показателями качества по переходной характеристике (рис. 3.17) 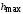 , ,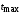 , , , , 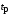 в общем случае невозможно, так как такая связь существует в конкретной форме для конкретной системы. Если речь идет о качественных показателях математической модели системы, то проблемы установления связи между различными показателями качества не существует. Имеющиеся в настоящее время компьютерные программы по моделированию для непрерывных САУ, позволяют быстро и с достаточной точностью определить значения всех известных показателей качества. Совсем по-другому ставится задача оценки показателей качества в процессе анализа и настройки существующей реальной САУ автоматизируемого объекта, на котором недопустимы эксперименты по снятию переходных характеристик. В связи с широким использованием в задачах анализа САУ частотных характеристик, особенно, логарифмических, которые часто могут быть получены экспериментальным путем, целесообразно иметь в распоряжении справочный материал в виде номограмм для определения основных показателей качества по параметрам ЛАЧХ разомкнутой системы. в общем случае невозможно, так как такая связь существует в конкретной форме для конкретной системы. Если речь идет о качественных показателях математической модели системы, то проблемы установления связи между различными показателями качества не существует. Имеющиеся в настоящее время компьютерные программы по моделированию для непрерывных САУ, позволяют быстро и с достаточной точностью определить значения всех известных показателей качества. Совсем по-другому ставится задача оценки показателей качества в процессе анализа и настройки существующей реальной САУ автоматизируемого объекта, на котором недопустимы эксперименты по снятию переходных характеристик. В связи с широким использованием в задачах анализа САУ частотных характеристик, особенно, логарифмических, которые часто могут быть получены экспериментальным путем, целесообразно иметь в распоряжении справочный материал в виде номограмм для определения основных показателей качества по параметрам ЛАЧХ разомкнутой системы.Установлена форма типовой логарифмической характеристики (рис. 3.21). Она характеризуется следующими параметрами: 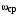 – частота среза ЛАЧХ разомкнутой системы; – частота среза ЛАЧХ разомкнутой системы; 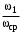 и и 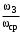 – относительные границы нижнечастотного и высокочастотного участков ЛАЧХ; – относительные границы нижнечастотного и высокочастотного участков ЛАЧХ; 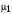 – усиление (в дБ) на частоте – усиление (в дБ) на частоте 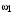 ; 40 дБ/дек, 60 дБ/дек – наклоны на участках ( ; 40 дБ/дек, 60 дБ/дек – наклоны на участках (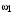 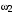 ) и ( ) и (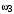 ). ).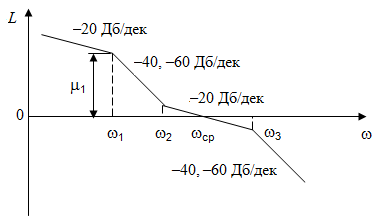 Рисунок 3.21. Типовая логарифмическая характеристика Вопросы для самопроверки Дайте определение устойчивости системы с физической и математической точек зрения. Какой характер имеет переходный процесс в устойчивой и неустойчивой системах? Сформулируйте необходимое условие устойчивости. Что такое критерии устойчивости? Что такое граница устойчивости? Каким образом при этом расположены корни характеристического уравнения системы на плоскости комплексного переменного? Сформулируйте критерий устойчивости Гурвица. Каким образом по критерию Гурвица определяются границы устойчивости? Сформулируйте критерий устойчивости Найквиста. Что такое запасы устойчивости? Каким образом они определяются по АФЧХ разомкнутой системы? Как определяются запасы устойчивости по ЛЧХ? Дайте понятие качества работы системы управления. Чем оно определяется? Что представляют собой критерии качества? Как производится оценка точности работы систем? Чему равны первые два коэффициента ошибок в системах с астатизмом первого и второго порядков? Определите показатели качества переходного процесса и частотные показатели, поясните их физический смысл. Поясните связь частотных показателей качества работы системы с частотными характеристиками разомкнутой цепи. Что представляют собой корневые оценки качества? В чем удобство и недостатки интегральных критериев качества? Каким образом экспериментальным путем можно оценить качество работы системы? 4. СИНТЕЗ ЛИНЕЙНЫХ САУ 4.1. Задачи и классификация методов синтеза Под синтезом САУ понимается выбор структуры и параметров системы управления, которые в соответствии с заданными техническими условиями обеспечивают наилучшие показатели по запасу устойчивости, по качеству переходных режимов и точности работы в установившихся режимах. В результате синтеза САУ решается одна из двух задач: 1) выбор структуры и параметров системы, если задано описание только объекта управления; 2) выбор количества и типа усилительных и корректирующих устройств, если заданы описания не только объекта управления, но и исполнительного органа системы управления, датчиков обратных связей и устройств сравнения. Параллельно с решением задач, перечисленных выше, рассматриваются и решаются вопросы, связанные с обеспечением надежности систем, весовых и стоимостных характеристик, экономичности и других подобных ограничений. Однако, решение подобного рода задач выходит за рамки теории автоматического управления и рассматривается в других технических дисциплинах. Следует отметить, что выполнение основных задач синтеза САУ: выбора структуры и параметров всей системы или ее части – представляет собой многовариантную и полностью неформализованную процедуру, что усложняет работу проектировщика, но в тоже время делает эту работу более творческой и привлекательной. В настоящее время известно множество методов синтеза линейных непрерывных и дискретных систем управления, которые различаются по: 1) математическому аппарату описания объекта и систем управления; 2) критериям качества работы САУ в установившихся и переходных режимах; 3) инструментальным средствам решения задач синтеза САУ. По используемому типу математической модели системы методы синтеза разделяются на: 1) методы, использующие описание в виде дифференциальных уравнений в обычной или матричной форме; 2) методы, использующие представление систем с помощью передаточных функций; 3) методы, базирующиеся на частотных характеристиках элементов и систем управления. По второму признаку методы синтеза разделяются, главным образом, по критериям качества в переходных режимах, так как определение параметров усилительных и регулирующих устройств, обеспечивающих заданные показатели точности работы в установившихся режимах, практически не отличается в различных методах синтеза. Таким образом, существуют следующие методы синтеза, использующие различные критерии качества в переходных режимах: метод В.В. Солодовникова, в котором критерием качества являются показатели переходной характеристики замкнутой скорректированной системы; метод В.А. Бесекерского, использующий в качестве критерия показатель колебательности замкнутой скорректированной системы; метод подчиненного управления, в котором настройки регуляторов рассчитываются по формулам, обеспечивающим приближение к единице амплитудно-частотной характеристики по управлению замкнутой синтезированной системы; метод модального управления, обеспечивающий достижение заданного распределения корней характеристического уравнения замкнутой синтезируемой системы управления. Следует заметить, что в рамках настоящей работы не упоминаются и не рассматриваются такие методы синтеза, как методы оптимального, экстремального и адаптивного управления, а также методы синтеза, например, по минимуму СКО (средне квадратичной ошибки), используемые для построения и расчета стохастических систем управления. Необходимые сведения по таким методам можно найти в специальных монографиях и пособиях по различным разделам теории автоматического управления. Отметим также, что первые два из перечисленных выше методов (Солодовникова и Бесекерского) считаются частотными, так как используют для синтеза понятие желаемой ЛАЧХ разомкнутой системы. Метод подчиненного управления оперирует с передаточными функциями, хотя часто для разъяснения и для большего понимания существа настройки оказывается необходимым привлечение аппарата частотных характеристик. Наконец, метод модального управления строится на использовании векторно-матричного описания синтезируемой системы. 4.2. Синтез желаемой ЛАЧХ разомкнутой системы В частотных методах синтеза по заданным показателям качества в переходных режимах (по переходной характеристике или по показателю колебательности) основным этапом синтеза является построение желаемой ЛАЧХ разомкнутой системы. Желаемой мы будем называть такую ЛАЧХ, достижение которой в системе обеспечит заданные в технических требованиях показатели по точности отработки оговоренных управляющих воздействий в установившихся и переходных режимах, а также степень подавления наиболее характерных для систем возмущающих воздействий. Отметим, что использование для синтеза САУ только ЛАЧХ без ФЧХ предполагает, что синтезируемая система является так называемой минимально-фазовой, т. е. 1) в системе отсутствуют звенья, передаточные функции которых имеют нули и полюса в правой полуплоскости; 2) для системы существует однозначная связь межу ЛАЧХ и ФЧХ. У ЛАЧХ разомкнутой системы, в том числе и у желаемой ЛАЧХ, принято различать три основные частотные области (рис. 4.1): область низких частот (НЧ) 0 1, область средних частот (СЧ) 2 3 и область высоких частот (ВЧ) 3 . 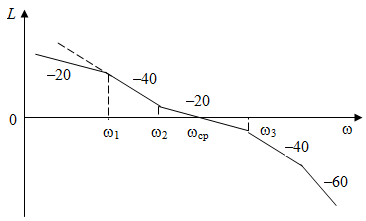 Рис. 4.1. Желаемая ЛАЧХ Как показали исследования, вид ЛАЧХ в области низких частот полностью определяет точность работы системы управления в установившихся режимах. Установившимися считаются режимы как при постоянном значении управляющего сигнала, так и при изменении его с постоянной скоростью или ускорением. Участок средних частот является определяющим для формы переходного процесса в системе, вызванного изменением параметра управляющего сигнала или приложением возмущающего воздействия. Для того чтобы обеспечить приемлемую по перерегулированию и по степени затухания переходную характеристику системы, участок средних частот должен иметь наклон –20 дБ/дек. Противоположность среднечастотного участка ЛАЧХ определяет степень затухания переходного процесса. Чем шире этот участок, тем более демпфирована система, меньше перерегулирование и время затухания переходного процесса. Наконец, участок высоких частот определяет степень подавления высокочастотных возмущений, действующих в системе, и с этой точки зрения значение ЛАЧХ в этой области должно быть как можно меньше. Переходные участки между областями, как правило, имеют наклон –40 дБ/дек, но иногда приходится допускать наклон –60 дБ/дек. 4.2.1. Синтез желаемой ЛАЧХ в области низких частот Как было отмечено выше, вид ЛАЧХ в области низких частот определяет точность замкнутой системы в установившихся режимах. Это значит, что для определения параметров нижнечастотного участка желаемой ЛАЧХ: наклона характеристики и коэффициента передачи разомкнутой системы на контрольной частоте, могут быть использованы результаты анализа установившихся ошибок при отработке различных типовых воздействий. Рассматрим порядок определения параметров нижнечастотного участка желаемой ЛАЧХ для систем различного порядка астатизма и различных управляющих и возмущающих воздействий. Статическая система (с астатизмом равным нулю) Статические системы в соответствии с результатами табл. 3.2 могут работать только со ступенчатыми управляющими сигналами и выдерживать только ступенчатые возмущения, поэтому параметры нижечастотной части желаемой ЛАЧХ должны определяться по ошибкам таких систем при отработке управляющих воздействий ступенчатой формы и ступенчатых возмущающих воздействий. Пусть задана ошибка при ступенчатом управлении 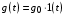 равная равная 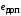 или в относительной форме или в относительной форме 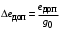 . Тогда, приравнивая допустимую ошибку ошибке установившегося режима . Тогда, приравнивая допустимую ошибку ошибке установившегося режима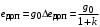 , ,и  меем меем 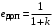 , откуда необходимый коэффициент разомкнутой системы , откуда необходимый коэффициент разомкнутой системы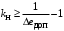 . . Нижнечастотный участок желаемой ЛАЧХ должен представлять прямую, параллельную оси частот (рис. 4.2) и удаленную от оси частот на 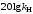 . . Следует заметить, что, если статическая система работает в режиме стабилизации с диапазоном 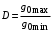 стабилизируемых значений, то необходимо использовать для расчета стабилизируемых значений, то необходимо использовать для расчета 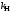 относительную ошибку относительную ошибку 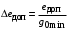 . .Теперь пусть задана относительная ошибка при отработке ступенчатого возмущающего воздействия 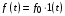 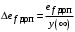 Приравняем 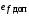 ошибке системы от возмущения ошибке системы от возмущения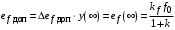 . .Кроме того примем 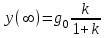 , что учитывает ошибку от управляющего сигнала. Тогда , что учитывает ошибку от управляющего сигнала. Тогда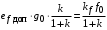 , ,откуда 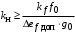 В этом случае 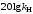 будет учитывать ошибки от управляющего и возмущающего воздействий, и, значит, нижнечастотный участок желаемой ЛАЧХ в виде прямой, удаленной от оси частот на будет учитывать ошибки от управляющего и возмущающего воздействий, и, значит, нижнечастотный участок желаемой ЛАЧХ в виде прямой, удаленной от оси частот на 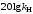 , будет построен с учетом необходимой точности при отработке и управляющего и возмущающего воздействий ступенчатой формы. , будет построен с учетом необходимой точности при отработке и управляющего и возмущающего воздействий ступенчатой формы.При расчете 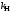 следует использовать следует использовать 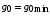 , если синтезируемая система будет работать в определенном диапазоне стабилизирующих значений , если синтезируемая система будет работать в определенном диапазоне стабилизирующих значений 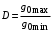 . .Астатическая система первого порядка Это наиболее распространенный тип систем управления, так как астатические системы первого порядка могут работать как следящие системы, системы программного управления, системы стабилизации. Поэтому целесообразно рассмотреть методику синтеза нижечастотного участка желаемой ЛАЧХ для различных типов управляющих воздействий. 1 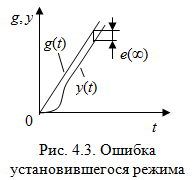 . Управляющее воздействие линейной формы . Управляющее воздействие линейной формы 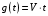 . Ошибка установившегося режима (рис. 4.3) . Ошибка установившегося режима (рис. 4.3) 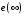 не должна превышать допустимую не должна превышать допустимую 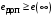 . .Известно, что 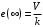 , где V – скорость изменения управляющего воздействия; k – общий коэффициент передачи разомкнутой системы, называемый добротностью по скорости. Тогда для опредения значения k необходимо чтобы ошибка , где V – скорость изменения управляющего воздействия; k – общий коэффициент передачи разомкнутой системы, называемый добротностью по скорости. Тогда для опредения значения k необходимо чтобы ошибка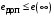 и и 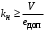 . .Н 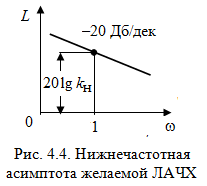 ижнечастотная асимптота желаемой ЛАЧХ (рис. 4.4) будет представлять собой прямую линию с наклоном ижнечастотная асимптота желаемой ЛАЧХ (рис. 4.4) будет представлять собой прямую линию с наклоном (20 дБ/дек) и проходящую через точку с координатами: 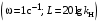 . .2. Управляющее воздействие синусоидальной формы 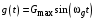 Ошибка установившегося режима 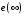 не должна превышать допустимого значения не должна превышать допустимого значения 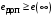 . .При синусоидальном управляющем сигнале ошибка также будет изменяться по синусоидальному закону 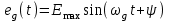 , ,где максимальное значение ошибки 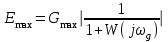 . .Полагая, что значение комплексной передаточной функции на частоте воздействия 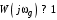 , получим , получим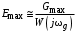 . . | |||||||||||||||||||