статитстика мухина. удмуртский государственный университет
 Скачать 313.62 Kb. Скачать 313.62 Kb.
|
|
Индекс структурных сдвигов отражает динамику среднего показателя лишь за счет изменения весов (при фиксировании индексируемой переменной на уровне базисного периода):
Между рассмотренными индексами существует следующая взаимосвязь: Ipпер.сост = Ipпост•Ipстр.сдв Задача № 5 составлена на вычисление уравнения взаимосвязи между исследуемыми признаками (факторным и результативным) и ее оценки при помощи парного (линейного) коэффициента корреляции, коэффициента детерминации и эмпирического корреляционного отношения. Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции 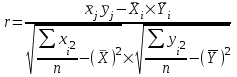 При линейной и нелинейной зависимости между признаками теснота связи между результативным и факторным признаками определяется с помощью эмпирического корреляционного отношения, которое рассчитывается по формуле  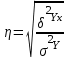 где 2Yx – вариация результативного признака под влиянием фактора Х (межгрупповая дисперсия); 2Y – вариация результативного признака под влиянием всех факторов (общая дисперсия). Эмпирическое корреляционное отношение может быть определено по формуле:   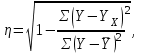 где Yх– теоретические значения результативного признака согласно полученному уравнению; Y – фактические значения факторного признака; 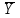 – средняя фактическая величина факторного признака. – средняя фактическая величина факторного признака.Чем ближе корреляционное отношение к 1, тем связь между признаками теснее, тем точнее полученная модель (уравнение регрессии) описывает эмпирические данные. Подкоренное выражение в теоретическом корреляционном отношении называется коэффициентом детерминации. Коэффициент детерминации показывает долю вариации результативного признака У под влиянием признака фактора Х. Вариант 1 Задача № 1 Имеются данные о числе зарегистрированных браков на 1000 чел населения и коэффициенте рождаемости в Удмуртской Республике в 2015 г.:
В целях изучения зависимости между коэффициентом браков и коэффициентом рождаемости произведите группировкуМО по коэффициенту браков, образовав пять групп районов с равными интервалами. По каждой группе подсчитайте: 1) число районов и городов; 2) средний размер коэффициент браков в расчете на один район; 3) средний размер коэффициента рождаемости в расчете на один район (МО). По данным коэффициента рождаемости определите общую дисперсию, межгрупповую и среднюю из групповых дисперсий, с помощью коэффициента детерминации определите влияние коэффициента браков на коэффициент рождаемости. Результаты представьте в виде групповой таблицы. Напишите краткие выводы. Задача № 2 Имеются следующие данные о товарообороте продовольственных магазинов розничной торговли:
Определите средний процент выполнения плана товарооборота: 1) в базисном году; 2) в отчетном году; 3) моду, средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение, коэффициент вариации данных отчетного года. Задача № 3 Имеются следующие количестве организаций в УР:
Для анализа динамики показателя количества организаций вычислите: 1) абсолютные приросты, темпы роста и темпы прироста по годам и к 2012 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в виде таблицы; 2) среднегодовые показатели: величину уровня ряда; абсолютный прирост, темп роста и прироста. Сделайте выводы. Постройте график динамики уровня ряда за период 2012-2016 гг., проведите аналитическое выравнивание ряда (постройте математическую модель и график), сделайте прогноз на 2017 и 2018 гг. Задача № 4 Имеются данные о потреблении населением товаров:
Определите: а) общий индекс стоимости потребления товаров населением; б) общий индекс физического объема потребления; в) общий индекс цен. Покажите взаимосвязь между индексами в абсолютном и относительном выражении. Задача № 5 Для изучения тесноты связи между коэффициентом рождаемости (результативный признак – у) и коэффициентом браков (факторный признак – х) вычислите по полученным средним показателям задачи №1 линейный коэффициент корреляции, коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение. Вариант 2 Задача № 1 Имеются следующие данные о стаже работы и средней месячной выработке рабочими ООО:
Для изучения зависимости между стажем работы и месячной выработкой продукции произведите группировку рабочих-сдельщиков по стажу, образовав пять групп рабочих с равными интервалами. По каждой группе подсчитайте: 1) число рабочих; 2) средний стаж работы; 3) среднюю месячную выработку продукции на одного рабочего. По данным месячной выработки определите общую дисперсию, межгрупповую и среднюю из групповых, с помощью коэффициента детерминации определите влияние стажа на выработку. Результаты представьте в виде групповой таблицы. Напишите краткие выводы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

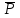 усл :
усл :