статитстика мухина. удмуртский государственный университет
 Скачать 313.62 Kb. Скачать 313.62 Kb.
|
Задача № 3 составлена на вычисление и усвоение аналитических показателей анализа динамических рядов. Для выражения изменений уровней ряда динамики в абсолютных величинах вычисляется показатель абсолютного прироста Y. Он показывает, на сколько единиц увеличился (или уменьшился) уровень по сравнению с базисным, то есть за определенный период времени. Абсолютный прирост определяется как разность между уровнем изучаемого периода Yi и уровнем, принимаемым за базу сравнения: Y = Yi – Yб . Абсолютные приросты могут быть цепными и базисными. При определении цепных абсолютных приростов Yu за базу сравнения принимается уровень предыдущего периода Yi–1, и расчет абсолютных приростов производится по формуле Yц = Yi –Yi – 1 . При определении базисных абсолютных приростов Yб за базу сравнения принимается постоянный уровень. Yб = Yi –Yб . Для суждения о среднем изменении абсолютных Yц приростов вычисляется средний абсолютный прирост 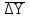 . Он может быть вычислен по цепным абсолютным приростам, базисным абсолютным приростам или уровнем ряда: . Он может быть вычислен по цепным абсолютным приростам, базисным абсолютным приростам или уровнем ряда:Yц 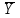 = ———, m = n – 1, = ———, m = n – 1,m где m – число интервалов в ряду динамики; YбnYn– Yб 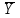 = ——, или = ——, или 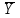 = ———, = ———,m m Относительными показателями динамики являются коэффициенты роста К и коэффициенты прироста К. Коэффициент роста показывает, во сколько раз увеличился уровень по сравнению с базисным или предыдущим уровнем. Он определяется как отношение уровня изучаемого периода к уровню, принятому за базу сравнения: Yi К = ––– . Yб Темп роста вычисляется в процентах и представляет собой произведение коэффициента роста на 100%, все преобразования коэффициентов роста сохраняются и для темпов роста. При вычислении цепных коэффициентов роста за базу сравнения принимается уровень предыдущего периода: Yi К ц = ––––– . Yi– 1 При вычислении базисных коэффициентов роста за базу сравнения принимают постоянный уровень (как правило, уровень самого раннего периода). Yi К б = ––– . Yб Между цепными и базисными коэффициентами роста существует определенная взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь соответствующий период: ПК ц = Кб, где П – знак произведения. Соблюдается связь (через коэффициенты). Для определения среднегодового коэффициента роста используется формула средней геометрической: 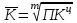 , ,где ПКц – произведение цепных темпов роста в коэффициентах; m – число цепных темпов роста (n– 1). Если при определении темпов прироста К предварительно были исчислены темпы роста Тр, то темпы прироста можно рассчитать по формуле: К = К – 1 или Тпр % = Тр% – 100%. Для средних темпов роста и прироста сохраняет силу та же взаимосвязь, имеющая место между обычными темпами роста и прироста: 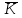 = = 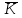 – 1 и – 1 и 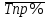 = = 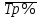 – 100%. – 100%.Показатель абсолютного значения одного процента прироста А% определяется как отношение в каждом периоде абсолютного прироста Yц к темпу прироста Кц. Расчет этого показателя имеет экономический смысл только на цепной основе: А%= Yц / К ц %. При разных уровнях явления абсолютное значение 1% является разной величиной. Аналитическое выравнивание рядасостоит в отыскании аналитической формулы кривой, которая наиболее точно отражала бы основную тенденцию изменения уровней в течение периода. Уравнение, выражающее уровни ряда динамики в виде некоторой функции времени, называют трендом. Аналитическое выравнивание ряда динамики позволяет выявить более четким направление основной тенденции. Рассмотрим технику выравнивания ряда по уравнению прямой. Параметры а0 и а1 искомой прямой определяются по методу наименьших квадратов. Составляется система нормальных уравнений:  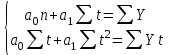 где t – порядковый номер интервала или момента времени. Расчет параметров а0и а1 упрощается, если за начало отсчета t = 0 принять центральный интервал или момент. Тогда t = 0, и система уравнений примет следующий вид: 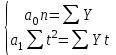
Аналитическое выравнивание ряда динамики позволяет выявить более четким направление основной тенденции. Для расчета параметров уравнения и проверки надежности уравнения необходимо построить вспомогательную таблицу: Исходные данные для расчета параметров линейной зависимости
Абсолютным показателем отклонения фактических уровней от тренда является среднее квадратическое отклонение (Y – Yt)2 = ————— . n Относительной мерой колеблемости служит модифицированный коэффициент вариации = —— • 100% . 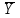 Показателем надежности полученных теоретических уровней Yt является эмпирическое корреляционное отношение 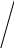   (Y – Yt )2 (Y – Yt )2 = 1 – —————, (Y – 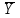 )2 )2где Yt – теоретические уровни ряда, согласно полученному тренду; Y – фактические значения уровня динамического ряда; 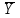 – средний уровень фактического динамического ряда. – средний уровень фактического динамического ряда.Чем ближе эмпирическое корреляционное отношение к 1, тем надежнее рассчитанное уравнение, и в этом случае его можно использовать для получения значения уровня будущего периода динамического ряда (экстраполировать). Задача № 4 составлена на усвоение индексного анализа динамики статистических показателей, состоящих из элементов, непосредственно не поддающихся суммированию и представляющих сложные социально-экономические явления. Общий агрегатный индекс состоит из: 1) индексируемой величины, характер изменения которой определяется; 2) соизмерителя, который называется весом. Для исчисления общих индексов необходимо привести их составные части к сопоставимому виду, когда веса в числителе и знаменателе берутся одинаковыми. Общий индекс цен p1q1 Ip = ——— , p0q1 где p1 и p0 – цена единицы продукции в отчетном и базисном периодах. Применение следующего индекса дает возможность оценить изменения физического объема продаж при сохранении цен неизменными, то есть не оказывающими влияния на динамику объема продаж. Общий индекс физического объема товарооборота q1p0 Iq = ——— . q0p0 Необходимо уяснить правило выбора веса для качественных (себестоимость, цена, урожайность и т.д.) и количественных (количество произведенной, проданной продукции, посевная площадь и т.д.) признаков при построении агрегатной формы общих индексов. Индексы объемных показателей рассчитываются по весам качественных показателей базисного периода. Индексы качественных показателей – по весам объемных показателей отчетного периода. В общем индексе стоимости товарооборота сопоставляются два стоимостных показателя: товарообороты отчетного и базисного периодов, поэтому индексируются оба элемента показателя. Общий индекс стоимости товарооборота p1q1 Ipq = ——– . p0q0 Между индексами существует взаимосвязь: Ipq = Ip•Iq . Средний арифметический и средний гармонический индексы Практическое их применение зависит от исходной статистической информации. Если у исходного агрегатного индекса условная величина в числителе дроби, то преобразуем в среднеарифметическую форму. Преобразование происходит за счет индивидуального индекса исследуемого показателя. Например, в индексе цен в знаменателе находится условная величина товарооборота отчетного периода по ценам базисного периода, поэтому в результате получаем среднегармонический индекс:
Агрегатный индекс физического объема содержит в числителе условный товарооборот отчетного периода в ценах базисного периода, поэтому можно преобразовать его в среднеарифметический индекс:
Применение индексов переменного, постоянного состава и структурных сдвигов служит для анализа динамики среднего уровня качественного показателя. Необходимость расчета этих индексов возникает в том случае, когда динамика средних показателей отражает не только изменение усредняемого признака, но и изменение структуры совокупности. Индекс переменного состава – это отношение средних величин качественного показателя. Например, индекс переменного состава имеет следующий вид:
Индекс переменного состава отражает динамику среднего показателя как за счет индексируемой величины, так и за счет изменения весов, по которым взвешивается средняя. Чтобы исключить влияние изменения структуры совокупности на динамику средних величин, можно для двух периодов рассчитать средние по одной и той же структуре. Такие средние называются стандартизованными, а их отношение представляет собой индекс постоянного (фиксированного) состава:
Этот индекс отражает динамику среднего показателя только за счет изменения индексируемой величины (при фиксировании весов на уровне отчетного периода). |

 1
1