Конспекты Алгебра 7 класс Мордкович. Урок 1 Числовые и алгебраические выражения

• Название: Урок 1 Числовые и алгебраические выражения
• Дата: 10.03.2023
• Размер: 0.64 Mb.
• Имя файла: Конспекты Алгебра 7 класс Мордкович.doc
• Тип: Урок; #978335
• страница: 1 из 8

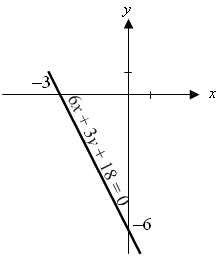
У р о к 1

Числовые и алгебраические выражения

Цель: повторяя материал курса математики 5–6 классов, ввести термины: математический язык, математическая модель, не давая им строгого обоснования; дать учащимся возможность привыкнуть к этим терминам и включить их в свой рабочий словарь, то есть заложить фундамент математического языка.

I. Актуализация опорных знаний учащихся.

1. Познакомить учащихся с основной идеей, объектами изучения, методами познания реальной действительности, возможностями нового учебного предмета – алгебры.

2. Познакомить учащихся с новым учебником, его концепцией, стилем изложения, со знаками, которые используются в учебнике.

3. Повторяя материал курса математики 5–6 классов, вспомнить определения и привести примеры:

а) числовых выражений;

б) алгебраических выражений;

в) порядка выполнения действий в числовых выражениях;

г) переместительного и сочетательного законов сложения и умножения;

д) понятия обыкновенной дроби, десятичной дроби, отрицательного числа;

е) арифметических операций с обыкновенными и десятичными дробями;

ж) основного свойства обыкновенной дроби;

з) правил действий с положительными и отрицательными числами.

4. Теоретический материал на тему «Числовые и алгебраические выражения» п. 1

Ведение конспекта.

II. Отработка практических знаний и навыков.

Устно № 1.1; 1.2; 1.4; 1.5.

Письменно № 1.6; 1.7; 1.10; 1.12, 1.13, 1.15-1.17

III. Задание на дом: § 1 вопросы, № 1.8; 1.9; 1.14.

У р о к 2

Числовые и алгебраические выражения

I. Организационный момент урока.

1. Опрос по теоретическому материалу предыдущего урока из п. 1.

2. Вспомнить с учащимися понятия:

а) значения числового выражения,

б) свойства нуля при выполнении различных арифметических действий.

II. Закрепление практических умений учащихся.

№ 1.19-1.22; 1.27, 1.30

Индивидуально в тетрадях №1.24, 1.25, 1.29, 1.32. С последующей проверкой друг друга.

III. Задание на дом: § 1 основные понятия, № 1.23; 1.26, 1.28.

У р о к 3

Числовые и алгебраические выражения

I. Актуализация опорных знаний учащихся.
1. Опрос по теоретическому материалу предыдущего урока из п. 1.
2. Работа у доски № 1.34, 1.38.
II. Самостоятельная работа.

III. Домашнее задание. № 1.36, 1.43 (б), 1.44 (б).

Самостоятельная работа

Числовые и алгебраические выражения

Вариант 1

1. Запишите в виде выражения :

а) сумму чисел 67,5 и 12,1;

б) произведение числа 5,2 и разности чисел 7,8 и 15,6.

2. Найдите значение выражения:

а) 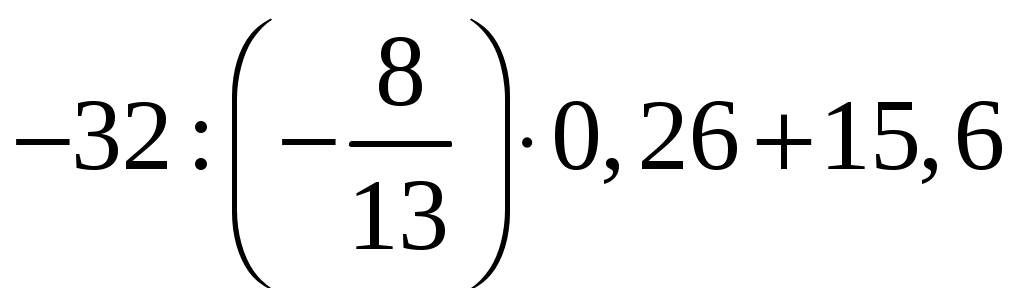; б) .

3. Найдите значение выражения .

4. Куплено 8 тетрадей по х рублей и 3 учебника по у рублей. Сколько стоит вся покупка? Составьте выражение.
Самостоятельная работа

Числовые и алгебраические выражения

Вариант 2
1. Запишите в виде выражения :

а) разность чисел 7,5 и 32,5;

б) произведение числа 15,3 и суммы чисел 9,8 и 1,5.

2. Найдите значение выражения:

а) 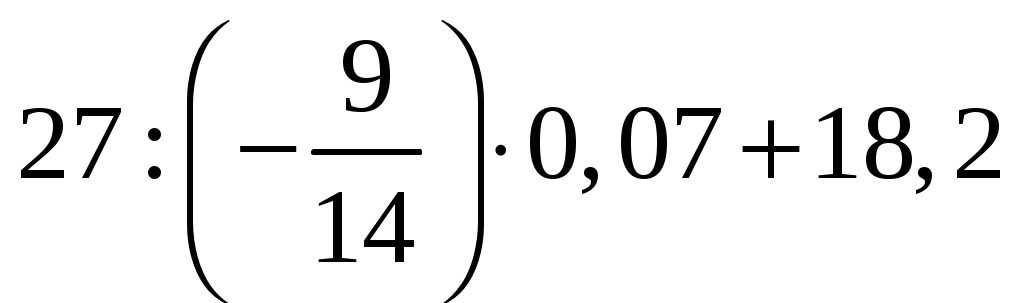; б) .

3. Найдите значение выражения .

4. Куплено 9 блокнотов по х рублей и 12 карандашей по у рублей. Сколько стоит вся покупка? Составьте выражение.

________

У р о к 4

Что такое математический язык

Цель: сформировать понимание учащимися того, что математика – предмет, позволяющий правильно ориентироваться в окружающей действительности; предмет, который реальные процессы описывает на особом математическом языке. Познакомить учащихся с некоторыми символами, правилами математического языка.
I. Опрос по теоретическому материалу предыдущего урока из п. 1.
II. Читать Параграф 2. Ведение конспекта. Основные понятия.

1. Выяснить, из чего состоит письменная и устная речь математического языка.

2. Вспомнить, с какими символами математического языка уже встречались учащиеся.

3. Познакомить учащихся с основами математического языка, которые будут ими изучаться в главах 1–5.

4. Обобщая новые сведения, попытаться сделать с учащимися вывод, что главное назначение математического языка – способствовать организации деятельности.

II. Отработка практических умений учащихся.

Устно: № 2.7; 2.8; 2.9; 2.10.

Письменно: № 2.4; 2.5; 2.6.

№ 2.11 – самостоятельно (один человек за доской для последующей проверки правильности выполнения задания).

III. Задание на дом: § 2. №2.11-2.13, 2.23. Основные понятия.

У р о к 5

Что такое математическая модель

Цель: сформировать понимание учащимися сути термина «математическое моделирование». Привести примеры, показывающие, как может математика описывать реальные процессы на особом математическом языке в виде математических моделей. Познакомить учащихся с тремя этапами математического моделирования и выработать умение применять полученные знания на практике.

I. Опрос по теоретическому материалу предыдущего урока из п. 2.

II. Изучение нового материала.

1.  Читать параграф 3. Вести конспект.

2. Для получения ответа на вопрос, зачем нужна математическая модель реальной ситуации, разобрать пример 1 из учебника.

3. Подвести итоги: выделить три этапа математического моделирования.

4. Для знакомства с еще одним видом математического моделирования разобрать пример 2 из учебника.

5. Повторить уже известные учащимся виды моделирования:

а) словесная модель;

б) алгебраическая модель;

в) графическая модель;

г) геометрическая модель.

II. Закрепление изученного материала.

Письменно у доски: № 3.1; 3.2; 3.3; 3.4; 3.7-3.17

III. Домашнее задание. п. 3 основные понятия, №3.6, 3.24, 3.30


У р о к 6

Что такое математическая модель

I. Опрос по теоретическому материалу предыдущего урока из п. 3.
II. Письменно у доски: № 3.41; 3.42.
III. Провести самостоятельную работу.

I в а р и а н т II в а р и а н т

№ 3.11; 3.17; 3.31(а) № 3.12; 3.15; 3.31 (в)

IV. Задание на дом: § 3. №3.41, 3.40, 3.47.

Линейное уравнение с одной переменной

Урок 7

Цель: повторить известные из курса 5–6 класса линейные уравнения с одной переменной, отработать алгоритм решения линейного уравнения.

I. Изучение нового материала.

1. Повторить алгоритм решения простых линейных уравнений. Рассмотреть реальную ситуацию (задача из задачника), позволяющую закрепить навыки решения уравнений с одной переменной.

2. Изучить, что называют решением уравнения и что значит решить уравнение.

II. Закрепление изученного материала.

Устно: № 4.1; 4.2; 4.11.

Письменно: № 4.2; 4.3; 4.7 (а, б); 4.9; 4.17.

III. Задание на дом: § 4, № 4.7 (в, г); 4.10; 4.4; 4.18.

Координатная прямая

Цель: повторить понятие координатной прямой (координатной оси), правило нахождения точки по заданной координате и правило отыскания координаты заданной точки. Познакомить учащихся с видами числовых промежутков. Обучить умению непринужденно связывать геометрическую и аналитическую модели промежутка и выбирать адекватное обозначение и символическую запись.

I. Изучение нового материала.

1. Повторить определение координатной прямой (координатной оси) и составляющих ее элементов (начало отсчета, масштаб; положительное направление).

2. На конкретных примерах с использованием таблиц, заготовленных заранее на плакатах, доске или кодопозитивах вспомнить правило нахождения точки по заданной координате и правило отыскания координаты заданной точки.

3. Используя таблицы на основе рисунков 10–19 учебника, изучить с учащимися виды числовых промежутков.

4. Результаты изучения видов числовых промежутков оформить в сводную таблицу, которую можно будет использовать при закреплении.

II. Закрепление изученного материала.

На первом уроке:

№ 5.1.

Устно: № 5.2; 5.3.

Самостоятельно (один человек за доской для последующей проверки правильности выполнения задания) № 5.5; 5.6.

№ 5.7–5.14 – буквы (в, г) в каждом из заданий.

№ 5.15; 5.16.

На втором уроке:

№ 5.17–5.19 буквы (в) в каждом из заданий.

Устно: № 5.20–5.25.

№ 5.28; 5.29.

Устно: № 5.30–5.35.

III. Задание на дом: § 21.

Урок 1: № 5.7–5.14; 5.4 – буквы (а, б) в каждом из заданий.

Урок 2: № 5.17–5.19 (буквы а, б); 5.26.

КООРДИНАТНАЯ ПЛОСКОСТЬ

Цель: повторить все термины, связанные с декартовыми прямоугольными координатами на плоскости. Изучить алгоритмы нахождения координат точки на плоскости и отыскания точки по ее координатам. Выработать умение пользоваться изученными алгоритмами.

I. Изучение нового материала.

1. Вспомнить с учащимися все изученные ранее термины, связанные с декартовыми прямоугольными координатами на плоскости: прямоугольная система координат; абсцисса, ордината, ось абсцисс, ось ординат; начало координат; координатные углы.

2. Изучить алгоритм отыскания координат точки М, заданной в прямоугольной системе координат.

3. Подробно и наглядно рассмотреть все возможные случаи расположения точек в координатной плоскости (в каждом из координатных углов и на каждой оси координат).

4. Изучить с учащимися особенности уравнений х = а и у = b и их графическое изображение.

5. Изучить алгоритм построения точки М (а; в) в прямоугольной системе координат.

II. Закрепление изученного материала.

На первом уроке:

Устно: № 6.1–6.3.

Письменно: № 6.9; 6.10; 6.12.

Самостоятельно № 6.13.

Устно: № 6.14–6.16.

Письменно: № 6.22; 6.28.

На втором уроке:

1) Устно: № 6.4–6.6.

Письменно: № 6.21.

№ 6.24 (в, г); 6.39 (а).

2) Провести самостоятельную работу.

I в а р и а н т II в а р и а н т

№ 6.32 (в) № 6.32 (г)

№ 6.40 (б) № 6.40 (а)

III. Задание на дом: § 6.

Урок 1: № 6.7; 6.8; 6.11.

Урок 2: № 6.23; 6.28; 6.31; 6.39 (б).

Линейное уравнение
с двумя переменными и его график

Цель: познакомить учащихся с линейным уравнением с двумя переменными. Выяснить, что является решением уравнения, что значит решить уравнение. Обучить учащихся строить график линейного уравнения с двумя переменными. Изучить алгоритм построения графика уравнения ax + by + c = 0. Обеспечить овладение основными алгоритмическими приемами построения графика уравнения ax + by + c = 0 и решения задач с помощью уравнений с двумя переменными.

I. Изучение нового материала.

1. Ввести понятие линейного уравнения с двумя переменными.

2. Рассмотреть реальную ситуацию (задача из учебника), позволяющую познакомить учащихся с линейным уравнением с двумя переменными.

3. Изучить, что называют решением уравнения и что значит найти его корни.

4. Акцентировать внимание учащихся на том, что не все решения линейного уравнения являются решениями задачи, по условию которой было составлено данное уравнение.

5. Разобрать пример 1 из учебника, с. 36.

6. Ввести понятие графика линейного уравнения ax + by + c = 0 и геометрической модели уравнения.

7. Разобрать и подробно оформить в тетрадях решение примера 2 из учебника.

8. Изучить и отработать алгоритм построения графика уравнения
ax + by + c = 0.

9. Выполнить пример 3 из учебника.

II. Закрепление изученного материала.

На первом уроке:

Устно: № 7.1; 7.5; 7.6.

Письменно: № 7.11; 7.14; 7.18 (в, г).

в)

1) если х = 0, то

;

3у = –18;

y = –6.

2) если у = 0, то ; x = –3. 3) построить на координатной плоскости хОу две точки (0; –6) и (– 3; 0). На втором уроке: Устная работа. 1. Является ли линейным уравнением с двумя переменными: а) ; б) у – x = 13; в) ; г) ?

2. Составьте какое-либо линейное уравнение с двумя переменными, решением которого служит пара чисел (5; – 2).

3. Решите уравнение:

а) ; б) 2,5x = 0;

в) 0x = 5; г) 0,1x = –2;

д) 0x = 0.

4. Устно: № 7.7.

Письменно: № 7.19; 7.20; 7.24.

б) 7s + 9t – 63 = 0

1) 7s = 63 – 9t; 2) 9t = 63 – 7s;

. .

№ 7.25; 7.27; 7.21.

На третьем уроке:

Устная работа.

1. Является ли решением уравнения x – 2y = 6 пара чисел:

а) (0;0); б) (2; –2); в) (8; 1);

г) (0; 3); д) (15; 4); е) (6; 0);

ж) (–5; 5,5)?

2. Выразите переменную у через переменную х из уравнения:

а) x + y = 1; б) 3x – y = 2; в) 2x + 5y = 10.

3. Точки А (…; 9), В (0; …), С (1; …), D (…; – 3) принадлежат графику уравнения 3x – y = 6.

Найдите пропущенные координаты.

III. Отработка практических умений.

1. Разобрать и оформить в тетрадях решение примера 4 из учебника.

2. Решить задачи.

№ 7.34; 7.22; 7.29.

IV. Задание на дом: § 7.

Урок 1: № 7.8; 7.10; 7.13; 7.17.

Урок 2: № 7.16; 7.23; 7.26.

Урок 3: № 7.31; 7.35.

Линейная функция и ее график

Цель: ознакомить учащихся с линейной функцией и ее графиком. Выработать у учащихся умение строить и читать график функции y = kx + b.

I. Изучение нового материала.

1. Повторить алгоритм построения графика уравнения ax + by + c = 0.

2. Помочь учащимся увидеть, что если это уравнение преобразовать к виду , а введя обозначения , , – к виду y = kx + m, то найти координаты точек соответствующей прямой удается легче и быстрее.

3. Изучить определение линейной функции.

4. Познакомить учащихся с понятиями независимая переменная и зависимая переменная.

5. Выяснить с учащимися, что является графиком линейной функции.

6. Разобрать пример 1, c. 44.

7. Разобрать три математические ситуации, приведенные в учебнике, и сделать вывод, что во многих случаях недостаточно составить математическую модель ситуации, необходимо еще очертить границы применимости модели.

8. Разобрать пример 2 из учебника и подробно оформить его решение в тетрадях.

9. Разобрать и оформить решение примера 3.

10. Ввести понятия наибольшее значение функции и наименьшее значение функции.

11. Разобрать пример 4 из учебника.

12. Разобрать пример 5 и ввести понятия и условия возрастания и убывания функции.