Конспекты Алгебра 7 класс Мордкович. Урок 1 Числовые и алгебраические выражения
 Скачать 0.64 Mb.
|
|
III. Задание на дом: § 39. Урок 1: № 39.11; 39.14. Урок 2: № 39.20; 39.29 (а); 39.31. Урок 3: № 39.35 (а, б); 39.33; 39.39. КОНТРОЛЬНАЯ РАБОТА Математический язык. Математическая модель Цель: проверить практические умения и навыки учащихся по изученной теме. (В а р и а н т) 1.  а)  б)  в)  .2. а) Если a = 3, b = 8, то (a + 2b)(2a – b) = (3 + 2 8)(2 3 – 8) = = 19 (–2) = –38. б) Если m = 15, k = 3, то  .3. x2 + a b. 4. (7x + 1) – (6x + 3) = 5. 7x + 1 – 6x – 3 = 5 x = 7 (7 7 + 1 ) – (6 7 + 3) = 50 – 45 = 5 Ответ: 7. 5. 0,6(x + 7) = 0,5(x – 3) + 6,8 0,6x + 4,2 = 0,5x – 1,3 + 6,8 0,6x – 0,5x = –4,2 – 1,3 + 6,8 0,1 = 1,3 x = 13 Ответ: 13. 6. а) (U + 2,4) t = 46. б)  ,если U = 20,6, то  .Ответ: а) (U + 2,4) t = 46; б) 2 часа. КОНТРОЛЬНАЯ РАБОТА Линейная функция Цель: проверка усвоения практических умений и навыков учащихся по темам «Линейная функция» и «Сокращение дробей». (В а р и а н т) 1. Сократите дробь: а)  ;б)  ;в)  .2. Построить график уравнения 5x + y – 4 = 0. Принадлежит ли ему точка С (–1,2; –10)? 1) Если x = 0, то y = 4. y = 0, то x = 0,8. 2) Так как 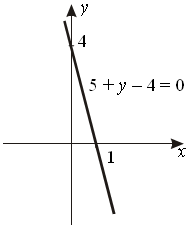 , то точка С (–1,2; –10) не принадлежит графику уравнения. 3. 5x + y – 4 = 0. а) y = –5x + 4; б) k = –5; b = 4. 4. Выделим на построенной прямой часть, соответствующую значениям х из отрезка [–1; 2]. С помощью рисунка делаем вывод: 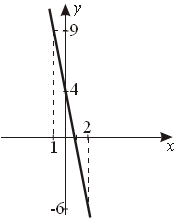 yнаиб = 9; yнаим = –6. 5. y = 3x – 2 y = –2x + 3 а)
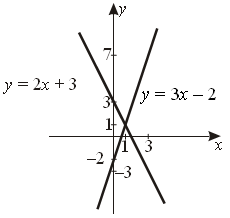 б) y = 3x – 2 y = –2x + 3   1 = 1 1 = 1 Ответ: (1; 1). 6. а) m = –3; б)  ;  .КОНТРОЛЬНАЯ РАБОТА Системы двух линейных уравнений с двумя переменными (В а р и а н т) 1. Решите систему уравнений методом подстановки:  Р е ш е н и е:  Ответ: (2; – 4). 2. Решите систему уравнений методом алгебраического сложения:  Р е ш е н и е:  Ответ: (– 3,5; – 3). 3. Решите графически систему уравнений:  Р е ш е н и е: y = 3x; y = 4x – 3
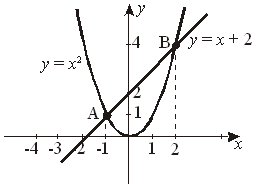
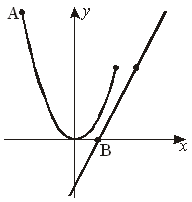
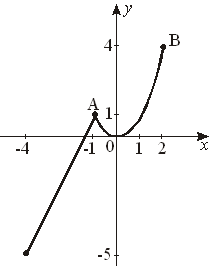
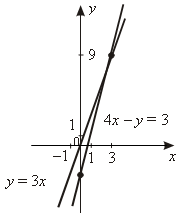 Ответ: (3; 9).4. Решите задачу, выделяя три этапа математического моделирования. Пусть в одной сетке было х баскетбольных мячей и у волейбольных мячей. В первый раз привезли 5х баскетбольных мячей и 2у волейбольных мячей, то есть всего 5x + 2y = 23. Во второй раз привезли 3х баскетбольных мячей и у волейбольных мячей. При этом баскетбольных мячей на 5 больше, чем волейбольных, то есть 3x – y = 5. Р е ш е н и е: Первый этап. Составим математическую модель ситуации:  Второй этап.  Третий этап. В каждой сетке было 3 баскетбольных и 4 волейбольных мяча. Ответ: 3 мяча баскетбольных; 4 мяча волейбольных. 5.  Ответ: –8; 5. КОНТРОЛЬНАЯ РАБОТА Степень с натуральным показателем и её свойства Цель: проверка практических умений и навыков учащихся по теме «Степень с натуральным показателем и ее свойства». (В а р и а н т) 1. Если x = –4, то  .2. а)  ; б)  ;в)  ; г)  ; д)  .3. а)  ;б)  ;в)  .4.  ; 5.  .6.  , т. е. m = 5, k = 2.КОНТРОЛЬНАЯ РАБОТА Одночлены. Арифметические операции над одночленами Цель: проверка умений и навыков учащихся по теме «Одночлены». (В а р и а н т) 1. а)  ;б)   .2. а)  ;б)  .3. а)  ; б)  .4.  .Если a =1,5, то  .5. Первый этап – составление математической модели. Пусть первый мальчик уничтожил на экране х ракет, тогда второй уничтожил (х + 3) ракеты, а третий – 2х ракет. Так как по условию всего они уничтожили 23 ракеты, то составим математическую модель задачи. x + x + 3 + 2x = 23. Второй этап – работа с составленной моделью. 4х + 3 = 23; 4х = 20; х = 5. Третий этап – ответ на вопрос задачи. Первый мальчик уничтожил 5 ракет, второй 5 + 3 = 8 ракет, а третий  ракет.Ответ: 5 ракет; 8 ракет; 10 ракет. КОНТРОЛЬНАЯ РАБОТА Многочлены. Арифметические операции над многочленами Цель: проверка знаний и практических умений и навыков учащихся по выполнению арифметических операций над многочленами. (В а р и а н т) 1. Если  и  , то а)   .б)   .2. а)  ;б)  ;3.  ; Ответ: 1. 4.  + 15 = a + 13. Если  , то a + 13 = –0,5 + 13 = 12,5.Ответ: а + 13; 12,5. 5. Пусть длина прямоугольника х см, тогда ширина (x – 3) см. После увеличения размеров прямоугольника его длина стала (x + 2) см, а ширина (x – 2) см. Так как по условию известно, что площадь прямоугольника увеличилась на 20 см3, то получим уравнение:  Получили x = 8, значит длина данного прямоугольника равна 8 см, а ширина – 5 см. Ответ: 8 см; 5 см КОНТРОЛЬНАЯ РАБОТА Формулы сокращенного умножения Цель: проверить практические навыки и умения учащихся по теме: «Формулы сокращенного умножения». (В а р и а н т) 1. а)  ;б)  ;в)  ;2. а)  3c – 7;б)  6ac == 3a2 + 3c2; в)  .3.  .Если а = –2, b = 10, то 4a2 – ab = 4 (–2)2 – (–2) 10 = 16 + 20 = 36. 4. I. Пусть первое натуральное число равное х, тогда второе равно (x + 1), а третье – (x + 2). Нам известно из условия, что квадрат большего из этих чисел на 37 больше произведения двух других чисел, значит получим уравнение: II. (x + 2)2 – x(x + 1) = 37; x2 + 4x + 4 – x2 – x = 37; x = 11. III. Мы получили x = 11, значит первое из чисел равно 11, второе – 12, а третье – 13. Ответ: 11, 12, 13 КОНТРОЛЬНАЯ РАБОТА Разложение многочленов на множители Цель: проверка усвоения изученного материала и умения выполнять разложение многочленов на множители различными способами. (В а р и а н т) Разложить на множители: 1. а)  ;б)  ;в)  .2. а)  ;б)  .3. а)  ;б)  ;в)  .4. Решить уравнение:   Ответ: –2; 2. 5. Вычислить:   КОНТРОЛЬНАЯ РАБОТА Функция у = х2 Цель: проверить усвоение учащимися практических умений сокращения дробей, навыков работы с графическими моделями. (В а р и а н т) 1. а)  .б)  .2. Решить графически уравнение x2 = x + 2. Р е ш е н и е: 1) y = x2 y = x + 2
Ответ: x1 = –1; x2 = 2. 3) а) А = В.
4. а) f(x + 1) = (x + 1)2 = x2 + 2x + 1; f(x + 3) = (x + 3)2 = x2 + 6x + 9; б) f(x + 1) = f(x + 3), если x2 + 2x + 1 = x2 + 6x + 9; 4x = –8; x = –2. Ответ: при х = –2.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
