Конспекты Алгебра 7 класс Мордкович. Урок 1 Числовые и алгебраические выражения

• Название: Урок 1 Числовые и алгебраические выражения
• Дата: 10.03.2023
• Размер: 0.64 Mb.
• Имя файла: Конспекты Алгебра 7 класс Мордкович.doc
• Тип: Урок; #978335
• страница: 2 из 8

II. Закрепление изученного материала.

На первом уроке:

Устно: № 8.1; 8.2; 8.9; 8.14 (в, г).

Письменно: № 8.15; 8.19.

На втором уроке:

Устно: № 8.4; 8.27.

Письменно: № 8.29; 8.32; 8.48; 8.52.

На третьем уроке:

Устная работа.

1. Является ли линейной функция, заданная формулой:

а) ; б) ;

в) ; г) ;

д) ?

Для этих формул укажите коэффициенты k и b.

2. Найдите координаты точки пересечения графика функции, заданной формулой y = 7x – 14, с: а) осью х; б) осью у.

Устно: № 8.62; 8.63.

Письменно: № 8.46; 8.50; 8.54; 8.57; 8.58; 8.61.

III. Задание на дом: § 8.

Урок 1: № 8.10; 8.14 (а, б); 8.17; 8.18.

Урок 2: № 8.28; 8.34; 8.47.

Урок 3: № 8.45; 8.53; 8.56; 8.60.

Линейная функция y = kx

Цель: ознакомить учащихся с прямой пропорциональностью, ее графиком и свойствами. Выработать у учащихся умение строить и читать график функции y = kx.

I. Изучение нового материала.

1. Ознакомить учащихся с прямой пропорциональностью.

2. Ввести понятие коэффициент пропорциональности.

3. Сформулировать и доказать теорему о графике прямой пропорциональности.

4. Обучить учащихся умению переходить от аналитической модели y = kx к геометрической и от геометрической к аналитической.

5. Выяснить с учащимися: как коэффициент пропорциональности влияет на угол, который прямая y = kx образует с положительным направлением оси х.

6. Ввести понятие угловой коэффициент.

7. Изучить теорему 4.

II. Закрепление изученного материала.

На первом уроке:

Устно: № 9.1; 92.

Письменно: № 9.3.

Самостоятельно № 9.4; 9.9; 9.11; 9.14.

На втором уроке:

Устно: № 9.5; 9.13.

Письменно: № 9.17; 9.15; 9.19.

III. Задание на дом: § 9.

Урок 1: 9.8; 9.10; 9.15.

Урок 2: № 9.12; 9.16; 9.18.

Взаимное расположение
графиков линейных функций

Цель: изучить, от чего зависит взаимное расположение графиков линейных функций. Выработать умение определять взаимное расположение графиков линейных функций.

I. Изучение нового материала.

1. Изучить теорему 5, c. 55.

2. Разобрать и оформить в тетрадях решение примеров 1 и 2 из учебника.

3. Изучить алгебраическое условие и геометрический вывод о взаимном расположении графиков линейных функций.

II. Закрепление изученного материала.

На первом уроке:

Устная работа.

1. Среди функций, заданных формулами y = x + 0,5; y = –0,5x + 4; y = 5x – 1; y = 0,5x + 1; , выделите те, графики которых параллельны графику функции y = 0,5x + 4.

2. № 10.1; 10.2.

Самостоятельно № 10.5; 10.6; 10.9.

На втором уроке:

Устная работа.

1. Задайте формулой линейную функцию, график которой параллелен графику функции y = 1,3x –7 и проходит:

а) через начало координат;

б) через точку С (0; 10).

2. График линейной функции – прямая, параллельная оси х. Задайте эту функцию формулой, если известно, что ее график проходит через точку:

а) А (1; –4); б) В (–5; 5); в) С (0; 3,5).

3. Устно: № 10.3.

Письменно: № 10.11; 10.12 (в, г); 10.19; 10.23.

III. Задание на дом: § 10.

Урок 1: № 10.4; 10.7; 10.8.

Урок 2: № 10.10; 10.12 (а, б); 10.18.

Основные понятия

Цель: сформировать представление о математической модели система уравнений. Изучить графический метод решения систем уравнений.

I. Актуализация опорных знаний учащихся.

Повторить с учащимися:

1) Понятие линейного уравнения с двумя переменными.

2) Привести примеры линейных уравнений с двумя переменными.

3) Что называют решением линейного уравнения с двумя переменными.

4) Является ли решением уравнения 2x – y = 3 пара чисел:

а) (0; – 3); б) (– 1; 1);

в) (4; 5); г) (1,5; 0).

5) Что является графиком линейного уравнения с двумя переменными, сколько решений может иметь уравнение ax + by + c = 0?

II. Изучение нового материала.

1. Сформировать у учащихся представление о математической модели система уравнений.

2. Познакомить учащихся с формой записи систем уравнений.

3. Изучить, что называют решением системы уравнений.

4. Изучить графический метод решения системы линейных уравнений, разобрать и оформить решения примеров 1, 2 и 3 из учебника.

5. Обобщить результаты решений этих примеров и сделать выводы о графическом методе решения систем уравнений:

а) что собой представляют графики обоих уравнений системы?

б) в каком случае система имеет единственное решение?

в) какая система является несовместимой?

г) о какой системе говорят, что она несовместима?

6. Подвести учащихся к пониманию того, что графический метод не всегда надежен и удобен, а значит, необходим алгебраический метод решения систем.

III. Закрепление изученного материала.

На первом уроке:

Устно: № 11.1; 11.2.

Самостоятельно № 11.3; 11.4; 11.6; 11.12; 11.13.

На втором уроке:

Устная работа.

1. При каком значении с график уравнения y = 3x + c проходит через точку:

А (– 4; 0); В (0;0); М (– 3; 1); К (0; – 8)?

2. Каково взаимное расположение на координатной плоскости графиков линейных функций:

а) y = –3x + 1 и y = 5x + 2;

б) y = 6x – 5 и y = 6x + 7?

Ответ обоснуйте.

3. Устно: № 11.8; 11.9.

Письменно: № 11.16; 11.17; 11.18; 11.20; 11.21.



Так как первое уравнение обращается в верное равенство при х = 5 и у = –3, можно найти значение а из соотношения .

Теперь можем решить систему уравнений.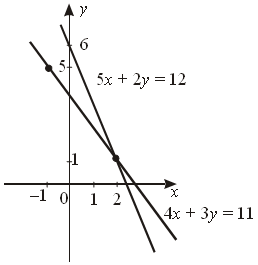





Ответ: (2; 1).

IV. Задание на дом: § 11.

Урок 1: № 11.7; 11.10.

Урок 2: № 11.15; 11.19.

Метод подстановки

Цель: сформировать у учащихся умение решать системы двух линейных уравнений методом подстановки. Обеспечить овладение всех учащихся основными алгоритмическими приемами этого метода.

I. Изучение нового материала.

1. Повторить этапы графического метода решения систем уравнений.

2. Вспомнить, какие выводы были сделаны на предыдущих уроках по этому методу.

3. Показать учащимся алгебраический метод решения примера 2 из предыдущего параграфа.

4. Изучить алгоритм решения системы двух уравнений с двумя переменными методом подстановки.

5. Разобрать и оформить в тетрадях решение примеров 1 и 2 из учебника.

II. Закрепление изученного материала.

На первом уроке:

Устная работа.

1. Является ли решением системы пара чисел:

а) (– 1; 1); б) (2; –1); в) (6; 2,5)?

2. Приведите пример уравнения с переменными х и у, равносильного линейному уравнению:

а) x – y = 3; б) ; в) .

3. Назовите три решения уравнения:

а) y = 2x + 5; б) xy = 0; в) x – y = 1;

г) ; д) .

4. № 12.5.

Письменная работа № 12.8; 12.9.

в)

1) Из первого уравнения x = 35 – 5y;

2) Подставим найденное выражение вместо х во второе уравнение системы и решим его:



3) ;

x = 5.

Ответ: (5; 6).

№ 12.9 (в, г).

На втором уроке:

I. Устная работа.

1. Решить систему уравнений

а)

б)

в)

2. Пересекает ли ось х график уравнения:

а) 7x – 9y = 1; б) y – x² = 9;

в) 3x – 0y = 5; г) 1,5y + 0x = 6;

д) 4x – y = 0?

3. № 12.6.

Письменно: № 12.14 (в, г); 12.15 (б, в, г); 12.16 (в, г).

Провести обучающую самостоятельную работу на III варианта по степени сложности.

I в а р и а н т

1. Выразите у через х:

а) x + y = 2; б) y – 6x = 1;

в) x – y = 4; г) 2y – x = 3.

2. Выразите х через у:

а) x + y = 6; б) x – 2y = 4;

в) 2y – x = 1; г) 3x – y = 2.

3. Выразите одну какую-либо переменную через другую:

а) x – 2y = 3;

б) 3x + y = 5;

в) 2y – x = 10.

4. Закончите решение системы:



y = 13 – 3x



II в а р и а н т

1. Выразите из уравнения одну переменную через другую:

а) 3x + y = 217; б) 5x – y = 17;

в) x + 6y = 4; г) 3x + 2y = 1.

2. Решая систему уравнений



ученик нашел, что х = 3, у = –2. Подставив вместо х и у найденные значения, проверьте, правильно ли решена система.

3. Решите способом подстановки систему уравнений:



Решение: x = y + 10.

2(y + 10) + 3y = 0 (закончите решение).

4. Решите систему уравнений способом подстановки и сделайте проверку:

а) б)

III в а р и а н т

1. Является ли пара чисел (– 3; 4) решением системы уравнений:

а)

б)

в)

2. Приведите уравнение к виду ax + by = c и выразите одну переменную через другую:

а) ;

б) .

3. Имеет ли данная система уравнений решения, и если имеет, то сколько:

а)

б)

в)

На третьем уроке:

I. Устная работа.

1. Являются ли системы линейных уравнений равносильными:

а) и

б) и

2. В какой точке прямая 7y – 4x = 28 пересекает:

а) ось х; б) ось у?

3. № 12.7

II. Решение систем уравнений.

1. Провести анализ результатов самостоятельной работы.

2. Выполнить № 12.19 (а, б).

г)









Ответ: (2; – 1).

№ 12.20 (в, г)

в)



Ответ: (– 6; 4).

На четвертом уроке:

1. № 12.21 (б, в, г); 12.22 (б, в, г).

2. Самостоятельная работа.

I в а р и а н т

Решите систему уравнений:

а) б)

в) г)

д) е)

Ответы: а) (2; 9); б) (– 2; 2); в) (7; – 3); г) (5; 8); д) (– 1; –1); е) (– 3; 0).

II в а р и а н т

Решите систему уравнений:

а) б)

в) г)

III в а р и а н т

Решите систему уравнений

а) б)

в) г)

Найдите координаты точек пересечения прямых:

y = 3,73x + 0,01 и y = 2,23x – 0,04.