Конспекты Алгебра 7 класс Мордкович. Урок 1 Числовые и алгебраические выражения
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
III. Задание на дом: § 33, № 33.6; 33.22; 33.29; 33.33 (а, б). У р о к 5 I. Устные упражнения. 1. Разложите на множители: а) a2x – a5x3; б) в) 25a2 – 10a + 1; г) a2 – ab – ac + a; д) 3(a + 2b) – a(a + 2b); е) 7x – 7y + a(y – x); ж) 3c2 + 15ac – 2c – 10a. 2. Найдите значение выражения 2ab + b2 + a2 при следующих парах значений переменных (a; b): а) (–2; 12); б) (5; –4); в) (4; 4); г) (3; –3). 3. Вычислите: а) 852 – 152; б) 882 – 122; в)  ; г) 61 59; ; г) 61 59;д) 2,1 1,9. II. Отработка практических умений. № 33.42 (в). в)  . .№ 33.44 (г). г) № 33.45 (б). б)   . .№ 33.49; 33.50. III. Задание на дом: § 33, № 33.32 (а, б); 33.40. У р о к 6 I. Устные упражнения. 1. Разложите на множители: а) x2 – 16y2; б) 4a2 + 12ab + 9b2; в) 2. Докажите, что при любом у значение выражения (y + 2)(y – 2) + 5 положительно. 3. Решите уравнение: а) x2 – 36 = 0; б) в) x2 – 0,6x + 0,09 = 0; г) x4 – 4x2 = 0. II. Отработка практических умений и навыков. № 33.43. № 33.47 (б, в). б)  в) № 33.48; 33.51. III. Задание на дом: § 33, № 33.8; 33.41; 33.52. Разложение многочленов на множители с помощью комбинации различных приемов Цель: выработать умение выполнять разложение многочленов на множители различными способами. На первом уроке: I. Актуализация опорных знаний учащихся. 1. Повторить формулы сокращенного умножения. 2. Вспомнить приемы разложения многочлена на множители, изученные в пятой главе. II. Отработка практических умений. 1. Разобрать и оформить в тетрадях решение примера 1 из учебника, с. 134. 2. Устно: № 34.1. 3. Письменно: № 34.3; 34.6; 34.8. № 34.9 (а, б). а) б) На втором уроке: I. Устная работа. 1. Разложите на множители: а) a2x – a5x3; б) в) 25a2 – 10a + 1; г) a2 – ab – ac + a; д) 3(a + 2b) – a(a + 2b); е) 7x – 7y + a(y – x); ж) 3c2 + 15ac – 2c – 10a. 2. Найдите значение выражения 2ab + b2 + a2 при следующих парах значений переменных (a; b): а) (–2; 12); б) (5; –4); в) (4; 4); г) (3; –3). II. Отработка практических умений. 1. Разобрать и оформить в тетрадях решение примера 2 из учебника. 2. Выполнить задания. № 34.12 (г). г) № 34.13 (в). в) – d)(c + 3 + d). № 34.24 (б). б) На третьем уроке: I. Устная работа. 1. Разложите на множители: а) x2 – 16y2; б) в) 4a2 + 12ab + 9b2. 2. Вычислите:  . .3. Докажите, что при любом значении у значение выражения (y + 2)(y – – 2) + 5 положительно. II. Отработка практических умений. 1. Разобрать и оформить в тетрадях решение примеров 3 и 4 из учебника. 2. Выполнить задания. № 34.14 (а). а) № 34.18 (а, б). а) б) № 34.19 (а). а) № 34.22 (в). в) На четвертом уроке: I. Устная работа. 1. В выражении a6 – вместо назовите такой одночлен, чтобы полученный двучлен можно было разложить: а) на два множителя; б) три множителя; в) четыре множителя. 2. Найдите все значения m, при которых верно равенство: (m – 6)2 = m – 6. II. Отработка практических умений. 1. Разобрать и оформить в тетрадях решение примеров 6 и 7 из учебника. 2. Выполнить задания. № 34.26 (в). в) 9z + 9 – z3 – z2 = 0;  Ответ: –3; –1; 3. № 34.28. Пусть а) в) г) № 34.14. III. Задание на дом: § 34. Урок 1: № 34.5; 34.7. Урок 2: № 34.10; 34.11; 34.23. Урок 3: 34.15; 34.17; 34.21. Урок 4: № 34.25. Домашняя контрольная работа I в а р и а н т II в а р и а н т Разложите на множители: 1) b(b + 1) – 3(b + 1); 1) y(a – b) + 2(a – b); 2) ca – cb + 2a – 2b; 2) 3x – 3y + ax – ay; 3) c2 – 0,25; 3) 4) x2 – 8x + 16; 4) b2 + 10b + 25; 5) 25x – x3; 5) y3 – 49y; 6) 2x2 – 20xy + 50. 6) –3a2 – 6ab – 3b2. Функция y = x2 и её график Цель: расширить знания учащихся о функциях. Продолжить совершенствование навыков чтения графиков на примере нелинейных функций. Научить строить и читать график функции y = x2. I. Изучение нового материала. 1. Познакомить учащихся с графическими моделями, отличными от линейной функции. 2. Построить график функции y = x2. 3. Исследовать свойства функции и особенности её графика. 4. Обратить внимание учащихся на вид графика вблизи начала координат и добиваться, чтобы учащиеся правильно выполняли построение графика (для значений х, близких к нулю, график практически сливается с прямой Ох). 5. Выработать у учащихся умение находить наибольшие и наименьшие значения функции на заданных промежутках. 6. Разобрать примеры 1 и 2 из учебника. 7. Познакомить учащихся с практическим применением свойств «фокуса параболы». II. Закрепление изученного материала. На первом уроке: Устно: № 37.1; 37.4. Устно с использованием таблицы, на которой изображен график функции y = x2. Устно: № 37.7; 37.8. Письменно: № 37.12; 37.13. Устно: № 37.14; 37.15; 37.18; 37.19. Письменно: № 37.24; 37.26 (а, б). На втором уроке: Устная работа. 1. Назовите координаты точек, симметричных точкам (2; 6); (–1; 4); (0;0); (–3;–5): а) относительно оси у; б) относительно начала координат. 2. Принадлежит ли точка (–2; 4) графику функции: а) y = x + 6; б) y = 2 – x; в) y = 3x + 2; г) y = x2; д) y = x2 + 4? 3. Определите без вычислений, какие из точек не принадлежат графику функции y = x2: (–1; 1); (–2; – 4); (0;8); (3; –9); (1,7; 2,89); (16; 0). Ответ обоснуйте. 4. Сколько общих точек могут иметь прямая и график функции y = x2? 5. Точка A(k; 6) принадлежит графику функции y = x2. Принадлежит ли этому графику точка: B(k; –6); C(–k; 6); M(–k; –6)? Ответ обоснуйте. Письменно: № 37.16; 37.17; 37.19. Найдите наибольшее и наименьшее значения функции y = x2 на заданном промежутке: 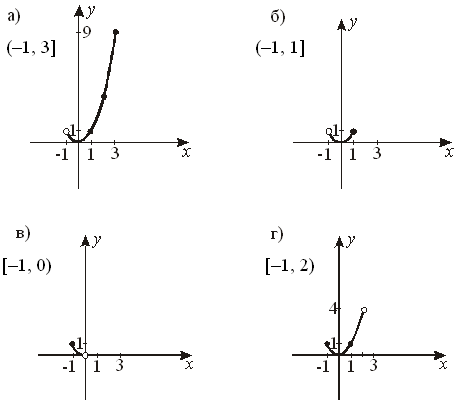 № 37,36; 37,38. № 37,42; 37,45; 37,48. III. Задание на дом: § 37. Урок 1: № 37,25; 37,26 (в, г); 37,32. Урок 2: № 37,33; 37,35; 37,41. Графическое решение уравнений Цель: обеспечить овладение учащихся основными алгоритмическими приемами графического решения уравнений. I. Изучение нового материала. 1. Вспомнить с учащимися, какие функции были изучены ранее, что представляют собой их графики. 2. Разобрать и оформить в тетрадях решение примера 1 из учебника. 3. Предложить учащимся сформулировать алгоритм графического решения уравнения, затем сравнить его с приведенным в учебнике. 4. Выполнить пример 2 из учебника. II. Закрепление изученного материала. На первом уроке: № 38.2; 38.3; 38.6. На втором уроке: № 38.9 (в, г); 38.10; 38.11. Решите графически уравнение: x2 = 1,5x – 6 1) y = x2; y = 1,5x – 6. 2) 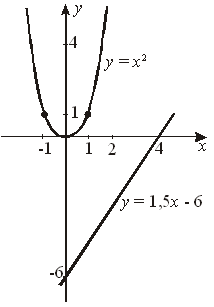 3) Точек пересечения у построенных парабол и прямой нет. Ответ: уравнение не имеет корней. III. Задание на дом: § 38. Урок 1: № 37.47; 38.1; 38.4. Урок 2: № 38.5; 38.7; 38.9 (а, б). Что означает в математике запись y = f(x) Цель: разъяснить смысл записи y = f(x), понятий: кусочные функции; область определения функции; непрерывность функции. Обеспечить овладение учащихся функциональной символикой и основными алгоритмическими приемами чтения графика. I. Изучение нового материала. 1. Познакомить учащихся с записью y = f(x) и ее смыслом. 2. Разобрать примеры 1 и 2 из учебника, с. 152. 3. Разобрав пример 3, познакомить учащихся с кусочными функциями. 4. Выполняя вычисления и построение графика кусочной функции (пример 4), сформировать у учащихся первые понятия об области определения функции и представление о чтении графика на наглядно-интуитивном уровне. 5. Изучить еще одно из свойств функции: непрерывность и разрыв графика функции. 6. Разобрать пример 5 из учебника. II. Закрепление изученного материала. На первом уроке: Устно: № 39.1. Письменно: № 39.2 (а); 39.6. f(x) = x2 а) f(–x) = (–x)2 = x2; б) f(x + 2) = (x + 2)2 = x2 + 4x + 4; в) f(5 – x) = (5 – x)2 = 25 – 10x + x2; г) f(2x + 3) – 9 = (2x + 3)2 – 9 = 4x2 + 12x + 9 – 9 = 4x2 + 12x. № 39.12. а) x = –5 удовлетворяет условию x < –1,3, значит f(x) = x + 5,7, следовательно f(–5) = –5 + 5,7 = 0,7. в) x = 0 удовлетворяет условию x ≥ –1,3, значит f(x) = –5, следовательно f(0) = –5. № 39.15. а)  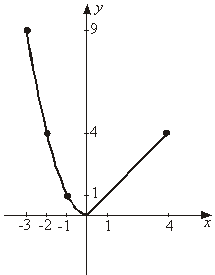
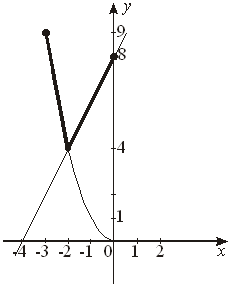 № 39.21. № 39.29 (б); 39.32; 39.36. Провести самостоятельную работу: I в а р и а н т: № 39.16 (а); 39.2 (в). II в а р и а н т: № 39.16 (б); 39.2 (г). На третьем уроке: № 39.34. а) 1. Область определения функции (–∞ ; +∞); 2. унаим. = 0 (достигается при х = 0); yнаиб. не существует. 3. Функция является непрерывной; 4. y = 0, если x = 0; y > 0, если x 5. Функция возрастает на луче [0; +∞); убывает на луче (–∞; 0]. № 39.36. № 39.40.  а) f(–1) = (–1)2 = 1; f(2) = 4; f(1) = 4 1 = 4; f(1,5) = 4; f(–2) = (–2)2 = 4. б) 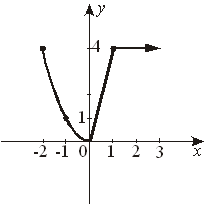 в) 1. Область определения функции [–2; 3]; 2. унаим. = 0 (достигается при х = 0); yнаиб. = 4 (достигается при х = – 2 и в любой точке полуинтервала [1; 3); 3. Функция является непрерывной; 4. y = 0, если x = 0; 5. y > 0, если x 6. Функция убывает на отрезке [–2; 0], возрастает на отрезке [0; 1] и постоянна в полуинтервале [1; 3). |