Урок 1 Числовые выражения

Название	Урок 1 Числовые выражения
Дата	09.03.2021
Размер	1.93 Mb.
Формат файла
Имя файла	1-63.doc
Тип	Урок #183094
страница	2 из 22

1 2 3 4 5 6 7 8 9 ... 22

Тема: Выражения с переменными.

Дата: 7.09.18 г

Цели: продолжить формировать умение находить значение выражения с переменными; формировать умение составлять выражение с переменными по условию задачи, в том числе формулы, и находить их значение.

Ход урока

I. Устная работа.

1. Назовите выражения, не имеющие смысла.

а) 2 · 4 – 8; б) 3 · 2 : (6 – 1,5 · 4); в)

;

г) 3 : 3 – 7 · 2; д)

; е)

;

ж) 2 : 4 – 2; з) 3 :

.

2. Найдите значение выражения 3а – b, если:

а) а = 2 и b = –4; б) а = 0 и b =

;

в) а = –4 и b = 5; г) а = –

и b =

.

3. Сколько процентов составляет:

а) 50 от 200; б) 13 от 260;

в) 1,5 от 20; г) 240 от 80?

II. Объяснение нового материала.

Вводится понятие формулы.Приведу примеры различных формул, применяемых на практике (вычисление площадей, объемов, числовые формулы и т. п.). Также следует объясняю что есть стабильные формулы, которые уже выведены и могут использоваться для расчетов. А есть задачи, для решения которых необходимо самостоятельно выявить закономерности (зависимости), описанные в условии, ввести переменные, составить выражение с переменными (формулу) и использовать его для вычисления искомого задачи при конкретных исходных данных.

III. Формирование умений и навыков.

1. № 29.

Решение:

Если площадь первого участка а га, а с каждого га собрали 32 ц пшеницы, то со всего участка собрали 32а ц пшеницы. Аналогично получаем для второго участка урожай 40b ц пшеницы. Тогда с обоих участков был собран урожай 32а + 40b (ц). Если а = 120 и b = 80, то 32а + + 40b = 32 · 120 + 40 · 80 = 3840 + 3200 = 7040.

Ответ: 32а + 40b (ц); 7040 ц.

2. № 31.

Решение:

Фигура состоит из отдельных частей. её площадь можно найти двумя способами:

1-й способ. «Разбить» фигуру на отдельные фигуры, для которых можно легко найти площадь, и, сложив полученные результаты, получить общую площадь.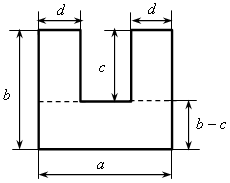

Площадь состоит из суммы площадей трех прямоугольников со сторонами: d и с; d и с; а и b – с. Их площади соответственно равны: сd; сd; а (b – с). Значит, площадь искомой фигуры составляет:

сd + сd + а (b – с) или 2сd + а (b – с).

Ответ: 2сd + а (b – с) (см²) или аb – с (а – 2d) (см²).

3. № 33.

Решение:

После добавления 5 г соли в раствор масса его стала равна 255 г. Масса чистой соли в растворе также увеличилась на 5 г и стала составлять (х + 5) г. Концентрация соли, таким образом, составляет

∙ 100 %.

Ответ:

∙ 100 %.

4. № 35 (устно); № 36 (устно).

.

iV. Итоги урока.

– Что называется значением выражения с переменными?

– В каком случае выражение с переменными не имеет смысла? Назовите выражение, которое содержит переменную х и которое не имеет смысла при х = –3,5.

– Назовите выражение, имеющее смысл при любых значениях входящей в него переменной у.

– Что представляет собой формула? Назовите формулу четного числа, нечетного числа.

Домашнее задание: 1. № 30, № 32, № 34, № 43.

Предмет: Алгебра

Класс: 7

Тема: Сравнение значений выражений

Дата: 7.09.18 г

Цели: формировать умение сравнивать значения числовых выражений, а также буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами при нахождении значений числовых выражений; ввести понятие двойного неравенства; формировать умение записывать результат сравнения выражений в виде двойного неравенства.

Ход урока

I. Организационный момент

Устная работа.

Опрос таблицы умножения.

II. Объяснение нового материала.

Рассмотрим задачу со с. 10 учебника. Она носит чисто практический характер, и её решение служит мотивацией изучения темы. Показываем учащимся, что при записи неравенства слева или справа (или в обеих частях) может стоять числовое выражение. Просим назвать неравенства.

Здесь следует напомнить, что неравенства бывают верные или неверные.

Задание. Определите, верно ли неравенство.

а) 3 · 15 > 8 : 2; б) 14 : 2 < –3 · 2;

в) 1,7 · 10 > 7 : 10; г)

< –2,5 ∙ 2.

Показываем на конкретных примерах, что если выражения содержат переменные, то для разных значений переменных результат сравнения значений этих выражений может оказаться различным.

Рассматриваем пример со с. 10 учебника. Также целесообразно попросить учащихся подобрать несколько значений переменной а, при которых будут верны либо не верны неравенства 2а > а + 4 и 2а < а + 4.

Вводим понятие двойного неравенства. Обращаем внимание на различные формулировки прочтения двойного неравенства.

III. Формирование умений и навыков.

1. Сравните значение выражений:

а)

; б)

;

в) 0,5 и

; г)

и –1,6;

д) 3,2 · 6,01 и 77,2 : 4; е) 38,4 : 6 и 12 – 5,6.

2. № 50.

3. № 48 (а; в); № 49 (а; б).

1. № 51; № 52 (устно).

2. Сравните значения выражений:

а) 2х + 5 при х = 0 и х = –1

;

б) 3 – 3а при а = 1 и а = –1;

в) 3х + 5у при х = –0,3, у = 0,6 и х = 1,2, у = –0,3;

г) 7а + b – 2c при а = 2, b = –4, с = 3 и а = –1,2, b = 0,4, с = 1.

3. Для выражений 25х + 1 и 800 : х – 99 составьте таблицу значений при х = 1; 2; 4; 5; 8. При каких из этих значений х:

а) первое выражение меньше второго;

б) первое выражение равно второму;

в) первое выражение больше второго?

Решение:

х	1	2	4	5	8
25х + 1	26	51	101	126	201
800 : х – 99	701	301	101	61	1

Ответ: а) 1; 2; б) 4; в) 5; 8.

1. № 56, № 57.

2. Какие числа, кратные 5, удовлетворяют неравенству:

а) 64 < х < 78; б) 405 < у < 450?

3. Запишите все числа х, у которых знаменатель дробной части 10, если

.

4. № 59.

IV. Итоги урока.

– В каком отношении могут находиться числовые выражения?

– Каким образом сравниваются выражения, содержащие переменные?

– Прочитайте неравенство:

а) –5 < х < –8; б) 15,7 < 15,9 < 16,2; в) –1 < 3

< 5,85.

Домашнее задание: № 47; № 48 (б; г); № 49 (в; г); № 53; № 54; № 58.

Урок №5
Сравнение значений выражений

Цели: продолжить формировать умение сравнивать значения числовых выражений, а также выражений с переменными при заданных значениях входящих в них переменных; ввести понятие строгого и нестрогого неравенства; формировать умение составлять выражения по условию задачи и сравнивать их значения.

Ход урока

I. Организационный момент

Устная работа.

1. Сколько процентов составляет: а) число 8 от числа 200; б) число 15 от числа 1500; в) число 24 от числа 12; г) число

от

?

2. Замените звездочку знаком: >, < или =.

а)

* 3; г) 32,5 – 12 * 4,01; б)

* 5 – 2,5; д) (5 – 2) · 7,5 * 5 – 2 · 7,5;

в) (–2) ∙

∙ 7 * – 3,5; е) –3,7 – 2,4 * –6,2.

3. Прочитайте неравенство:

а) 3,7 < 3,8 < 3,95; в) –b < –a < – c; б) k < p < 2k; г)

.

II. Проверочная работа.

Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите в виде двойного неравенства: t положительно и меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.

III. Объяснение нового материала.

Вводится понятие строгого и нестрогого неравенства на конкретных примерах (число дней в месяце, количество пассажиров в автобусе, предельные температуры и т. п.).

Определение. Неравенства, составленные с помощью знаков > и <, называют строгими неравенствами, а неравенства, составленные с помощью знаков ≥ и ≤, называют нестрогими.

Необходимо подчеркнуть, что нестрогое неравенство является верным, если выполняется хотя бы одно соотношение:

18 ≥ 14 – верно (выполняется 18 > 14);

–35 ≤ –35 – верно (выполняется –35 = –35).

Если не выполняется ни одно из соотношений, то неравенство является неверным:

–35 ≥ –34.

Двойные неравенства также могут быть записаны с помощью знаков ≥ и ≤:

18 ≤ х ≤ 19; 1,7 < п ≤ 1,8;

.

IV. Формирование умений и навыков.

1. № 60 (устно); № 61 (устно).

2. Задание по вариантам.

Запишите каждое предложение с помощью знаков неравенства. Подберите три значения переменной, при которых данное неравенство верно, и три, при которых неверно.

Вариант 1

1) а) t меньше 5;

б) р больше или равно –11,3;

в) т – неотрицательное число;

2) а) х меньше 5 и больше или равно 4;

б) а больше 0,01 и меньше 0,02;

в) с больше или равно –0,7 и отрицательно.

Вариант 2

1) а) t больше 7;

б) υ меньше или равно –1,17;

в) р – неположительное число;

2) а) b меньше 8 и больше или равно –7;

б) а меньше 0,07 и больше 0,06;

в) q меньше или равно 0,1 и положительно.

3. Расположите числа в порядке возрастания.

.

4. Расположите числа в порядке убывания.

(0,3)²; 0,3; (0,3)³.

1. Один сплав состоит из 5 кг олова и 15 кг меди, другой – из 3 кг олова и 7 кг меди. В каком из сплавов процентное содержание меди больше?

При решении задач на проценты нужно использовать наглядное изображение данных, что в дальнейшем позволит учащимся грамотно выполнять анализ условия текстовых задач, решаемых алгебраическим методом.

Решение: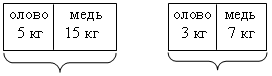

20 кг 10 кг

1) Масса первого сплава равна 20 кг, второго – 10 кг.

2) Выразим процентное содержание меди в первом и во втором сплавах:

∙ 100 % = 75 % и

∙ 100 % = 70 %.

3) 75 > 70, значит, в первом сплаве процентное содержание меди больше.

Ответ: в первом сплаве.

2. № 65.

Решение:

Средняя скорость автомобиля «Жигули» равна

км/ч, а автомобиля «Москвич» –

км/ч. Сравним средние скорости автомобилей:

а) Если х = 12,5, у =10,5, то

= 56, а

= 60. То есть при данных значениях переменных верно неравенство

.

б) Если х = у = 14, то

= 50, а

= 45. То есть при данных значениях переменных верно неравенство

.

Ответ: а) Средняя скорость автомобиля «Жигули» меньше. б) Средняя скорость автомобиля «Жигули» больше.

V. Итоги урока.

– Какое неравенство называется строгим? Приведите примеры.

– Какое неравенство называется нестрогим? Приведите примеры.

– Когда верно нестрогое неравенство? Когда оно не верно? Приведите примеры.

Домашнее задание: 1. № 62, № 63, № 64.

Вариант 1

1) а) t меньше 5;

б) р больше или равно –11,3;

в) т – неотрицательное число;

2) а) х меньше 5 и больше или равно 4;

б) а больше 0,01 и меньше 0,02;

в) с больше или равно –0,7 и отрицательно.

Вариант 2

1) а) t больше 7;

б) υ меньше или равно –1,17;

в) р – неположительное число;

2) а) b меньше 8 и больше или равно –7;

б) а меньше 0,07 и больше 0,06;

в) q меньше или равно 0,1 и положительно.

Вариант 1

1) а) t меньше 5;

б) р больше или равно –11,3;

в) т – неотрицательное число;

2) а) х меньше 5 и больше или равно 4;

б) а больше 0,01 и меньше 0,02;

в) с больше или равно –0,7 и отрицательно.
Вариант 2

1) а) t больше 7;

б) υ меньше или равно –1,17;

в) р – неположительное число;

2) а) b меньше 8 и больше или равно –7;

б) а меньше 0,07 и больше 0,06;

в) q меньше или равно 0,1 и положительно.

Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите в виде двойного неравенства: t положительно и меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.

Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите в виде двойного неравенства: t положительно и меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.

Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите в виде двойного неравенства: t положительно и меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.
Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите в виде двойного неравенства: t положительно и меньше 45.

Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.
Вариант 1

1. Сравните значения выражений:

1) 3х – 6,2 и 2х – 1,8 при х = –4; х = 4,4;

2) 2a – 3b и 3a – 2b при а = –2 и b = 3.

2. Запишите в виде двойного неравенства: t положительно и меньше 45.
Вариант 2

1. Сравните значения выражений:

1) 5х + 11 и 3х – 6 при х = 2; х = –8,5;

2) 3a + 2b и 2a – 3b при а = –2 и b = 4.

2. Запишите в виде двойного неравенства: р отрицательно и больше –18.

Урок №6

Предмет: Алгебра

Класс: 7

1 2 3 4 5 6 7 8 9 ... 22