Урок 1 Числовые выражения
 Скачать 1.93 Mb. Скачать 1.93 Mb.
|
|
Тема: ЧТО ТАКОЕ ФУНКЦИЯ? Дата: 05.10.19 г Цели: ввести понятие функциональной зависимости; дать определения независимой переменной (аргумента), зависимой переменной, области определения функции, области значений функции. Ход урока Организационный момент I. Анализ контрольной работы. 1. Решите уравнение. а) б) 6x – 10,2 = 0; г) 2x – (6x – 5) = 45. 2. Таня в школу сначала едет на автобусе, а потом идет пешком. Вся дорога у неё занимает 26 мин. Идет она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе? 3. На одном участке было в 5 раз больше саженцев смородины, чем на другом. После того как с первого участка увезли 50 саженцев, а на второй посадили еще 90, на обоих участках саженцев стало поровну. Сколько всего саженцев было на двух участках первоначально? 4. Решите уравнение 6x – (2x – 5) = 2(2x + 4). II. Объяснение нового материала. 1. Основная задача первого занятия: показать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами. Функция имеет общекультурное, мировоззренческое значение. При её изучении учащиеся знакомятся с идеей всеобщей связи, идеей непрерывности, бесконечности, интерполяции. 2. Объяснение проводить согласно пункту 12 учебника. Необходимо привести достаточно примеров функциональной зависимости (учебник, с. 51–53). Также нужно не только показывать зависимости, но и сразу обсуждать, в какой области человеческой деятельности применяются такие функциональные зависимости. 3. Вводим понятия независимой и зависимой переменных и определение функции как зависимости одной переменной от другой. На примерах показываем, что область определения функции может быть бесконечным и конечным множеством чисел. III. Формирование умений и навыков. Все задания, решаемые на этом уроке, направлены на усвоение как самого понятия функции, так и различных способов её задания (словесный, с помощью формулы, табличный, графический). Ученики должны уметь переходить от одного вида задания к другому и находить значения функции при каждом способе задания. 1. № 258, № 260. 2. Функция задана формулой у = 2 – 5х, верны ли равенства: а) у = 12 при х = –2; б) у = 3 при х = в) у = 20 при х = 4; г) у = –0,5 при х = 3. № 261. 4. Функция задана графиком: 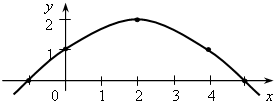 а) Найти значения функции при х = 0; 2; 3,5; –1. б) При каком значении х значение функции равно 1; 2; 0? в) Назвать несколько значений х, при которых значение функции положительно. г) Назвать несколько значений х, при которых значение функции отрицательно. 5. Устно. Результаты измерений температуры воздуха за сутки даны в следующей таблице:
а) Назовите температуру в 6 ч, 8 ч, 24 ч. б) В какое время температура была равна +1°, –4°, 11°? в) Почему эту зависимость можно назвать функцией? IV. Итоги урока. – Что называется функцией? – Что называется аргументом? – Какими способами можно задать функцию? Назовите преимущества каждого из них. Домашнее задание: № 259; № 262; № 264. Предмет: Алгебра Класс: 7 Тема: Вычисление значений функции по формуле Цели: продолжить работу по усвоению понятия функции и связанных с функцией понятий (область определения функции, область значений функции и др.); формировать умение находить значения функций, заданных аналитически (с помощью формулы). Ход урока I.Организационный момент Устная работа. Опрос таблицы умножения; таблицы квадратов II. Объяснение нового материала. Цель этого и последующих занятий – в упорядочении имеющихся представлений о функции, развертывании системы понятий, характерных для функциональной линии. Значительное место должно быть отведено усвоению важного представления – однозначности соответствия аргумента и определенного по нему значения функции. Для рассмотрения этого вопроса привлекаются различные способы задания функции. Чаще других в математике и её приложениях применяется задание функции формулой. Все другие способы играют подчиненную роль. Однако сопоставление разных способов задания выполняет важную роль: 1) и таблицы, и графики служат для удобного в определенных обстоятельствах представления функции, имеющей аналитическую форму записи; 2) необходимо для усвоения всего многообразия аспектов понятия функции. Объяснение проводить согласно пункту 13 учебника. Разбираем пример № 1 со с. 55 учебника. Показываем, что для того, чтобы найти значение функции, необходимо подставить некоторое значение аргумента в формулу. Также объясняем, что в случае, когда область определения функции явно не задана, считают, что она состоит из всех значений независимой переменной, при которых эта формула имеет смысл. III. Формирование умений и навыков. 1. № 267. 2. Вычислить значение следующих функций при х, равном –2; –1; 0; 1; 2. а) у = 3х; б) у = –2х; в) у = –х – 3; г) у = 20х + 4. 2-я группа. 1. № 270. 2. № 271.Решение: у = х (х – 3,5)
1. Найдите область определения функции, заданной формулой: а) у = 3х + 2; б) у = г) у = Физминутка для рук. 2. № 351.Решение: а) у = Область определения функции – все числа, кроме тех, при которых х – 4 = 0, то есть х2 = 4. Значит, не входят в ООФ х = 2 и х = –2. б) у = Область определения функции – все числа, кроме тех, при которых х2 + 4 = 0, то есть х2 = –4. Уравнение не имеет решения, значит, ООФ – любое число. Ответ: а) любое число, кроме 2 и –2; б) любое число. 3. Дополнительные задания (для сильных учащихся). 3.1. Найдите область определения функции. а) у =  б) у =  3.2. Задайте формулой какую-нибудь функцию, область определения которой: а) все действительные числа; б) все действительные числа, кроме –11; в) все действительные числа, кроме 3 и 5; г) все неотрицательные действительные числа; д) все неположительные действительные числа.; е) только одно число. IV. Итоги урока. - Какую тему мы проходим; - Что означает найти область определения. Домашнее задание: 1. № 268; № 269; № 272. Предмет: Алгебра Класс: 7 Тема: Вычисление значений функции по формуле Цели: продолжить формировать умение находить значение функции по формуле, а также формировать умение находить значение аргумента, соответствующее заданному значению функцию, умение решать практические задачи с использованием функциональной терминологии. Ход урока I. Организационный момент Устная работа. 1. Найдите значение функции у = 2х – 1 для значений аргумента, равного 0; 1; 2; –1. 2. Найдите область определения функции: а) у = 3х – 7; б) у = II. Формирование умений и навыков. 1. № 273, № 274. 2. Функция задана формулой у = 2х – 1. а) Какое значение у соответствует х, равному 10; –4,5; 15; 251; 600? б) При каком значении х соответствующее значение у равно: –19; –57; 205; –3 Решение: а) Если х = 10, то у = 2 · 10 – 1 = 19; если х = –4,5, то у = 2 · (–4,5) – 1 = –10; если х = 15, то у = 2 · 15 – 1 = 29; если х = 251, то у = 2 · 251 – 1 = 501; если х = 600, то у = 2 · 600 – 1 = 1199. б) Если у = –19, то 2х – 1 = –19; 2х = –19 + 1; 2х = –18; х = –9; то есть у = –19, при х = –9. Если у = –57, то 2х – 1 = –57; 2х = –57 + 1; 2х = –56; х = – 28, то есть у = –57 при х = – 28. Если у = 205, то 2х – 1 = 205; 2х = 205 + 1; 2х = 206; х = 103, то есть у = 205 при х = 103. Если у = –3 2х = –3,5 + 1; 2х = –2,5; х = –1,25, то есть у = –3 1. Из формулы равномерного движения s = υt выразить скорость υ как функцию пути s и времени t. Вычислить по этой формуле среднюю скорость полета пули, если s = 3 км, t = 6 с. 2. № 276.Решение: Обозначим за т массу пробки в граммах, а за V – объем в см3. Тогда зависимость массы куска пробки от объема можно выразить формулой т = 0,18 · V. а) Если V = 240, то т = 0,18 · 240 = 43,2 (г); б) если т = 64,8, то 0,18 · V = 64,18; V = 64,18 : 0,18; V = 360 (см3). Ответ: а) 43,2 г; б) 360 см3. 3. № 278.Решение: Анализ условия: 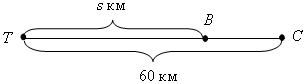 s = 12 · t. а) Если t = 3,5, то s = 12 · 3,5 = 42 (км); б) если s = 30, то 12 · t = 30; t = 30 : 12; t = 2,5 (ч). Ответ: а) 42 км; б) 2,5 ч. 4. № 352.Решение: Анализ условия: у = 1,5х + 150. а) если х = 10, то у = 1,5 · 10 + 150 = 15 + 150 = 165; б) если у = 180, то 1,5х + 150 = 180; 1,5х = 180 – 150; 1,5х = 30; х = 30 : 1,5; х = 20, значит, у = 180 при х = 20. Ответ: а) у = 165; б) х = 20. III. Проверочная работа. Вариант 1 1. Функция задана формулой у = 3х – 7. Найдите значение аргумента, при котором значение функции равно нулю. 2. Найдите значение аргумента, при котором функция у = –3х – 2 принимает значение 0,3. 3. Запишите область определения функции, заданной формулой у = Вариант 2 1. Функция задана формулой у = 5 + 2х. Найдите значение аргумента, при котором значение функции равно нулю. 2. Найдите значение аргумента, при котором функция у = –5х + 11 принимает значение 0,2. 3. Запишите область определения функции, заданной формулой у = IV. Итоги урока. – Дайте определение функции. Что называется аргументом, значением функции? – Объясните на примере функции, заданной формулой у = 3х + 18 Домашнее задание: № 275; № 277; № 279; № 353. Предмет: Алгебра Класс: 7 Тема: График функции. Цели: продолжить формировать умения строить график функции и находить значение функции по заданному аргументу с помощью графика; формировать умение интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы практической задачи. Ход урока I. Проверочная работа. Вариант 1 1. Найдите значения функции, заданной формулой у = 2. Найдите значение аргумента, при котором функция у = 4х + 3 принимает значение, равное Вариант 2 1. Найдите значения функции, заданной формулой у = 2. Найдите значение аргумента, при котором функция у = 5х + 4 принимает значение, равное 1,5. II. Устная работа. На рисунке изображен график зависимости некоторой величины у от некоторой величины х. 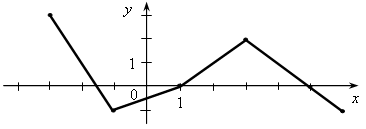 Ответьте на вопросы: а) Чему равное значение у, если х = –3; –1; 2; 5? б) Чему равны значения х, если у = 3; 0; 1? в) Какое минимальное и какое максимальное значения принимает величина у? III. Формирование умений и навыков. 1. № 283. Можно задать учащимся дополнительные вопросы: а) Сколько точек пересечения с осью х имеет график? Каково значение у в этих точках? б) Сколько точек пересечения с осью у имеет график? Каково значение х в этой точке? в) Сравните значения функции в точках –2 и 1. г) Назовите координаты какой-нибудь точки графика, у которой значения аргумента и функции положительны; значение аргумента положительно, а функции – отрицательно и т. д. Физминутка зарядка для кистей рук. 2. № 284, № 285. 3. Используя график функции, заполните таблицу значений функции для –2 ≤ х ≤ 3 с шагом 0,5.  IV. Итоги урока. – Что называется графиком функции? – Как построить график функции, заданной формулой? – Как по графику найти значение функции, соответствующее данному значению аргумента? – Как по графику функции найти значение аргумента, которому соответствует данное значение функции? – Как по графику зависимости определить, является ли она функцией? Домашнее задание: № 355; № 356 Предмет: Алгебра Класс: 7 |
