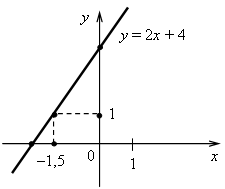Урок 1 Числовые выражения

Название	Урок 1 Числовые выражения
Дата	09.03.2021
Размер	1.93 Mb.
Формат файла
Имя файла	1-63.doc
Тип	Урок #183094
страница	11 из 22

1 ... 7 8 9 10 11 12 13 14 ... 22

Тема: линейная функция и её график

Дата: 06.11.18 г

Цели: обобщить и систематизировать знания по теме «Линейная функция»; подготовиться к написанию контрольной работы.

Ход урока

I. Игра-слалом.

Класс разбивается на 3 команды. Игра состоит из теоретического и практического конкурсов. Задания выполняются на время. Побеждает команда, получившая наибольшее число правильных ответов за наименьшее время.

1. Теоретический конкурс

1. Какую зависимость называют функциональной или функцией?

2. Что такое аргумент и что такое функция?

3. Что называют областью определения функции?

4. Что такое график функции?

5. Какую функцию называют линейной?

6. Что является графиком линейной функции?

7. Что является графиком прямой пропорциональности?

8. В чём их сходство и различие?

9. От чего зависит расположение графика линейной функции?

10. Сколько точек необходимо для построения графика линейной функции?

11. А для графика прямой пропорциональности? Почему?

12. Что такое угловой коэффициент?

13. Как расположен график функции y = kx при k > 0 и k < 0?

14. Как найти координаты точки пересечения графиков двух линейных функций?

15. В каком случае графики двух линейных функций являются параллельными прямыми?

2. Практический конкурс

1. Функция задана формулой у = 5х + 18. Определите:

а) значение у, если х = 0,4;

б) значение х, при котором у = 3;

в) проходит ли график функции через точку С (–6; –12).

2. а) Постройте график функции у = 2х + 4.

б) Укажите с помощью графика, чему равно значение у при х = –1,5.

3. В одной и той же системе координат постройте графики функций:

а) у = –0,5х; б) у = 5.

4. Найдите координаты точки пересечения графиков функций
у = –14х + 32 и у = 26х – 8.

5. Задайте формулой линейную функцию, график которой параллелен прямой у = 2х + 9 и проходит через начало координат.

1. у = 5х + 18.

а) Если х = 0,4, то у = 5 · 0,4 + 18 = 2 + 18 = 20;

б) если у = 3, то 5х + 18 = 3;

5х = 3 – 18;

5х = –15;

х = –15 : 5;

х = –3;

в) –12 = 5 · (–6) + 18;

–12 = –30 + 18;

–12 = –12 – верно, значит, график функции проходит через точку
С (–6; –12).

Ответ: а) 20; б) –3; в) проходит.

2. а) у = 2х + 4.

Построим две точки, принадлежащие графику.

Если х = 0, то у = 2 · 0 + 4 = 4;

если х = –2, то 2 · (–2) + 4 = 0.

(0; 4), (–2; 0)

б) Если х = –1,5, то у = 1.

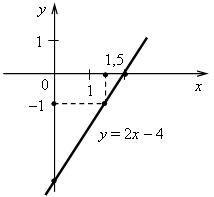
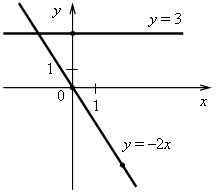
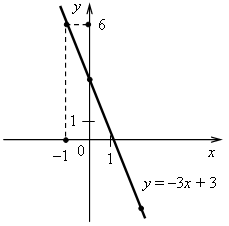
3. а) у = –0,5х. Графиком является прямая, проходящая через начало координат и точку (4; –2).

б) у = 5. Графиком является прямая, проходящая через точку (0; 5) и параллельная оси х.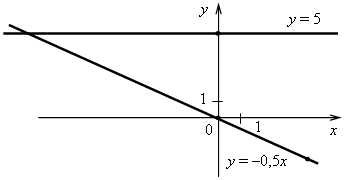

4. Решим уравнение:

–14х + 32 = 26х – 8;

–14х – 26х = –8 – 32;

–40х = –40;

х = 1, значит, абсцисса точки пересечения графиков равна 1. Найдем соответствующее значение ординаты:

если х = 1, то у = –14 · 1 + 32 = 18.

Точка пересечения имеет координаты (1; 18).

Ответ: (1; 18).

5. График параллелен прямой у = 2х + 9, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 2х.

Ответ: у = 2х.

II. Итоги урока.

Домашнее задание: повторить п. 15, п. 16. № 360; № 363; № 372.

Урок 40

Контрольная работа № 3

Вариант 1

1. Функция задана формулой у = 6х + 19. Определите:

а) значение у, если х = 0,5;

б) значение х, при котором у = 1;

в) проходит ли график функции через точку А (–2; 7).

2. а) Постройте график функции у = 2х – 4.

б) Укажите с помощью графика, чему равно значение у при х = 1,5.

3. В одной и той же системе координат постройте графики функций:

а) у = –2х; б) у = 3.

4. Найдите координаты точки пересечения графиков функций
у = 47х – 37 и у = –13х + 23.

5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат.

Вариант 2

1. Функция задана формулой у = 4х – 30. Определите:

а) значение у, если х = –2,5;

б) значение х, при котором у = –6;

в) проходит ли график функции через точку В (7; –3).

2. а) Постройте график функции у = –3х + 3.

б) Укажите с помощью графика, при каком значении х значение у равно 6.

3. В одной и той же системе координат постройте графики функций:

а) у = 0,5х; б) у = –4.

4. Найдите координаты точки пересечения графиков функций
у = –38х + 15 и у = –21х – 36.

5. Задайте формулой линейную функцию, график которой параллелен прямой у = –5х + 8 и проходит через начало координат.

Вариант 3

1. Функция задана формулой у = 5х + 18. Определите:

а) значение у, если х = 0,4;

б) значение х, при котором у = 3;

в) проходит ли график функции через точку С (–6; –12).

2. а) Постройте график функции у = 2х + 4.

б) Укажите с помощью графика, чему равно значение у при х = –1,5.

3. В одной и той же системе координат постройте графики функций:

а) у = –0,5х; б) у = 5.

4. Найдите координаты точки пересечения графиков функций
у = –14х + 32 и у = 26х – 8.

5. Задайте формулой линейную функцию, график которой параллелен прямой у = 2х + 9 и проходит через начало координат.

Вариант 4

1. Функция задана формулой у = 2х – 15. Определите:

а) значение у, если х = –3,5;

б) значение х, при котором у = –5;

в) проходит ли график функции через точку K (10; –5).

2. а) Постройте график функции у = –3х – 3.

б) Укажите с помощью графика, при каком значении х значение у равно –6.

3. В одной и той же системе координат постройте график функций:

а) у = 2х; б) у = –4.

4. Найдите координаты точки пересечения графиков функций
у = –10х – 9 и у = –24х + 19.

5. Задайте формулой линейную функцию, график которой параллелен прямой у = –8х + 11 и проходит через начало координат.

Рекомендации по оцениванию.

Задания 1–3 относятся к базовому уровню знаний по теме. Верное выполнение любых трех заданий оценивается отметкой «3». Для получения отметки «5» необходимо выполнить верно все пять заданий.

Решение заданий контрольной работы

Вариант 1

1. у = 6х + 19.

а) Если х = 0,5, то у = 6 · 0,5 + 19 = 3 + 19 = 22;

б) если у = 1, то 6х + 19 = 1;

6х = 1 – 19;

6х = –18;

х = –18 : 6;

х = –3;

в) 7 = 6 · (–2) + 19;

7 = –12 + 19;

7 = 7 – верно, значит, график функции проходит через точку
А (–2; 7).

Ответ: а) 22; б) –3; в) проходит.

2. а) у = 2х – 4. Построим две точки, принадлежащие графику. Если х = 0, то у = 2 · 0 – 4 = –4; если х = 2, то у = 2 · 2 – 4 = 0. (0; –4), (2; 0). б) При х = 1,5 у = –1.
3. а) у = –2х. Графиком является прямая, проходящая через начало координат и точку (2; –4). б) у = 3. Графиком является прямая, проходящая через точку (0; 3) и параллельная оси х. 4. Решим уравнение: 47х – 37 = –13х + 23. 47х + 13х = 23 + 37;

60х = 60;

х = 1, значит, абсцисса точки пересечения графиков функций равна 1. Найдем соответствующее значение ординаты:

если х = 1, то у = 47 · 1 – 37 = 10.

Точка пересечения имеет координаты (1; 10).

Ответ: (1; 10).

5. График параллелен прямой у = 3х – 7, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 3х.

Ответ: у = 3х.

Вариант 2

1. у = 4х – 30.

а) Если х = –2,5, то у = 4 · (–2,5) – 30 = –10 – 30 = –40;

б) если у = –6, то 4х – 30 = –6;

4х = –6 + 30;

4х = 24;

х = 24 : 4;

х = 6;

в) –3 = 4 · 7 – 30;

–3 = 28 – 30;

–3 = –2 – неверно, значит, график функции не проходит через точку В (7; –3).

Ответ: а) –40; б) 6; в) не проходит.

2. а) у = –3х + 3.

Построим две точки, принадлежащие графику.

Если х = 0, то у = –3 · 0 + 3 = 3;

если х = 2, то у = –3 · 2 + 3 = –3;

(0; 3), (2; –3)
б) Если у = 6, то х = –1.

3. а) у = 0,5х. Графиком является прямая, проходящая через начало координат и точку (4; 2).

б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.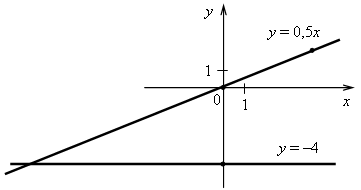

4. Решим уравнение:

–38х + 15 = –21х – 36;

–38х + 21х = –36 – 15;

–17х = –51;

х = (–51) : (–17);

х = 3, значит, абсцисса точки пересечения графиков функций равна 3.

Найдем соответствующее значение ординаты:

если х = 3, то у = –38 · 3 + 15 = –99.

Точка пересечения имеет координаты (3; –99).

Ответ: (3; –99).

5. График параллелен прямой у = –5х + 8, значит, угловые координаты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = –5х.

Ответ: у = –5х.

Вариант 3

1. у = 5х + 18.

а) Если х = 0,4, то у = 5 · 0,4 + 18 = 2 + 18 = 20;

б) если у = 3, то 5х + 18 = 3;

5х = 3 – 18;

5х = –15;

х = –15 : 5;

х = –3;

в) –12 = 5 · (–6) + 18;

–12 = –30 + 18;

–12 = –12 – верно, значит, график функции проходит через точку
С (–6; –12).

Ответ: а) 20; б) –3; в) проходит.

2. а) у = –3х – 3. Построим две точки, принадлежащие графику: если х = 0, то у = –3 · 0 – 3 = –3; если х = –2, то у = (–3) · (–2) – 3 = 3. (0; –3), (–2; 3). б) Если у = –6, то х = 1.
3. а) у = 2х. Графиком является прямая, проходящая через начало координат и точку (2; 4). б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.

4. Решим уравнение:

–10х – 9 = –24х + 19;

–10х + 24х = 19 + 9;

14х = 28;

х = 28 : 14;

х = 2, значит, абсцисса точки пересечения графиков равна 2. Найдем соответствующее значение ординаты:

если х = 2, то у = –10 · 2 – 9 = –29.

Точка пересечения имеет координаты (2; –29).

Ответ: (2; –29).

5. График параллелен прямой у = –8х + 11, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это – прямая пропорциональность. Значит, у = –8х.

Ответ: у = –8х.
Урок №39

Предмет: Алгебра

Класс: 7

Тема: Определение степени с натуральным показателем

Дата: 09.11.18 г

Цели: ввести понятие степени числа а с натуральным показателем п; определить значение степени с натуральным показателем положительного и отрицательного числа в зависимости от четности / нечетности показателя степени; формировать умение вычислять значение степени и представлять число в виде степени с натуральным показателем.

Ход урока

I. Организационный момент

Устная работа.

Вычислите.

а) 3 · 45; б)

· 120; в)

;

г)

; д)

· 49; е) –3 · (–16);

ж) –(–3) · 12; з) –(2 · (–9)); и)

;

к) 18 ·

+ 11; л)

· (11 – 6); м)

.

II. Объяснение нового материала.

1. Объяснение проводить согласно пункту 18 учебника. Напоминаем, что вместо длинной записи произведения 5 · 5 · 5 · 5 · 5 · 5 · 5 можно записать выражение 5⁷, где 5 – основание степени (повторяющийся множитель), а 7 – показатель степени (число повторяющихся множителей).

Понятие степени определяем для любого числа а в качестве основания и любого натурального показателя (аналитическая запись).

На доску выносится запись:

Степенью числа а с натуральным показателем п, большим 1, называется выражение а^п, равное произведению п множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а.

Проговариваем с учащимися правило чтения степени, приводим примеры.

2. Мини-лабораторная работа.

Найдите значение степени.

3³; 3⁴; 3⁵; 3⁶; 0¹;

; 0²;

(0,1)²; (0,1)³; (0,1)⁴; (0,1)⁵; 0³;

(–2)²; (–2)³; (–2)⁴; (–2)⁵; 0⁴;

; 0⁵;

(–0,1)²; (–0,1)³; (–0,1)⁴; (–0,1)⁵; 0⁶.

Задания разбиваем либо по группам, либо раздаем индивидуально. Затем «по цепочке» ученики выходят к доске и записывают результаты.

После анализа полученных результатов на доску выносятся следующие правила:

При возведении в степень положительного числа получается положительное число.

При возведении в степень нуля получается нуль.

Степень отрицательного числа с четным показателем – положительное число.

Степень отрицательного числа с нечетным показателем – отрицательное число.

Обособленно выносим правило для квадратов чисел (пропедевтика изучения решения квадратных уравнений):

Квадрат любого числа есть положительное число либо нуль (а² ≥ 0 при любом а).

3. Рассматриваем примеры 1–3 со с. 88–89 учебника.

III. Формирование умений и навыков.

№ 374, № 375 (устно), № 376, № 378, № 380.

При выполнении этих заданий учащиеся должны четко называть степень, можно просить назвать их основание и показатель степени.

1. № 382, № 381 (а, б).

2. Не выполняя вычислений, сравните значение данного выражения с нулем:

а) (–4,1) · (–5,6)⁶; б) (–3,3)³ : (–5,7);

в) –(4,8)² · (–1,2)⁴; г) –(–2,7)⁴ · (–6,4)⁵.

3. Сравните значения выражений:

а) (–6,5)⁴ и (–2,4)³;

б) (–0,2)⁶ и (–0,2)¹⁰;

в) (–1,5)⁷ и (–1,5)⁹.

3-я группа

№ 384, 385 (а, в, г), 386 (а, в, д, ж), 387 (а, б, в).

IV. Итоги урока.

– Сформулируйте определение степени числа с натуральным показателем. Приведите примеры и назовите в каждом из них основание и показатель степени.

– Чему равна первая степень любого числа?

– Какой знак имеет результат возведения положительного числа в натуральную степень?

– Какой знак имеет значение степени отрицательного числа с четным показателем? С нечетным показателем?

– Каков порядок действий при нахождении значения выражения, содержащего степени с натуральным показателем?

Домашнее задание: № 377; 379; 381 (в, г); 383.

Урок 40

Определение степени с натуральным показателем

Цели: продолжить формировать умение вычислять значение числового выражения, содержащего степень; формировать умение вычислять значение буквенного выражения, содержащего степень, и решать практические задачи с использованием понятия степени с натуральным показателем.

Ход урока

I. Математический диктант.

Вариант 1

1. Запишите в виде произведения третью степень числа 4 и найдите её числовое значение.

2. Чему равна первая степень числа –5?

3. Вычислите значение выражения 2³ · 0,5.

4. Чему равна сумма кубов чисел 5 и 3?

5. Вычислите значение выражения (–3)² + (0,1)³.

Вариант 2

1. Запишите в виде произведения четвертую степень числа 3 и найдите её числовое значение.

2. Чему равна первая степень числа

?

3. Вычислите значение выражения 3² · 0,7.

4. Чему равен квадрат разности чисел 7 и 5?

5. вычислите значение выражения (–5)³ – (0,2)².

II. Актуализация знаний.

№ 387 (г, д, е, ж, з, и), № 388.

№ 388.

Решение:

а) –1³ + (–2)³ = –1 + (–8) = –9;

б) –6² – (–1)⁴ = –36 – 1 = –37;

в) –8³ + (–3)³ = –512 + (–27) = –539;

г) 10 – 5 · 2⁴ = 10 – 5 · 16 = 10 – 80 = –70;

д) 2 · 3⁴ – 3 · 2⁴ = 2 · 81 – 3 · 16 = 162 – 48 = 114;

е) 2 · 5³ + 5 · 2³ = 2 · 125 + 5 · 8 = 250 + 40 = 290;

ж) 3⁴ –

= 81 – 1 = 80;

з) 0,2 · 3² – 0,4 · 2⁴ = 0,2 · 3² – 0,2 · 2 · 2⁴ = 0,2(3² – 2 · 2⁴) =
= 0,2(9 – 2 · 16) = 0,2 · (9 – 32) = 0,2 · (–23) = –4,6;

и) 8 · 0,5³ + 25 · 0,2² = 2 ³ · 0,5³ + 5² · 0,2² = (2 · 0,5)³ + (5 · 0,2)² =
= 1³ + 1² = 1 + 1 = 2.

При выполнении этого упражнения учащиеся выводят правило:

aⁿ · bⁿ = (a · b)ⁿ, для любых a и b.

III. Формирование умений и навыков.

На этом уроке отрабатывается умение вычислять значение буквенного выражения, содержащего степень.

1-й блок

1. Найдите значения выражений х²; – х²; х² – 4 для заданных значений х и заполните таблицу (используйте найденные значения выражения х² для вычисления значений двух других выражений):

х	–5	–2,5	0	0,3	1	12
х²
–х²
х² – 4

2. Найдите значение выражений х³; 0,1х³; х³ + 10 для заданных значений х и заполните таблицу:

х	–4	–0,3	–1	0	9
х³
0,1х³
х³ + 10

3. № 392 (устно).

2-й блок

1. Найдите значение выражения.

а) (ху)² при х = 12 и у = –0,5; х = –14 и у = –1;

б)

при х = –6 и у = 1,5; х = 0 и у = –23;

в) (х + у)⁴ при х = 0,7 и у = 0,3; х = –11 и у = 6;

г) (у – х)³ при х = –14 и у = –10; х = 0,9 и у = 1,1.

2. № 393.

3. Сравните значения выражений.

а) –а² и (–а)² при а = 3; –5; 0;

б) –а³ и (–а)³ при а = 10; –2; 0.

4. № 395.

Решение:

а) а³ · а = (а · а · а) · а = а⁴;

б) а⁴ · а² = (а · а · а · а) · (а · а) = а⁶;

в) а³ · а⁶ =

= а⁹;

г) а²⁰ · а¹² =

= а³².

№ 396, № 397.

3-й блок

1. № 389.

2. Сколько биений сделает сердце человека за сутки, если за 1 мин оно делает в среднем 75 биений?

3. Может ли школьник поднять 1 м³ пробки? (Масса 1 см³ пробки 0,2 г.)

Решение:

Рассчитаем, сколько см³ в 1 м³:

1 м³ = 1 · 1 · 1 ( в м) = 100 · 100 · 100 (в см) = 1 000 000 = 10⁶ см³.

Масса 1 м³ пробки равна 0,2 · 10⁶ (г), что составляет 200 000 г или 200 кг. Значит, школьник не сможет поднять такую массу.

Ответ: нет.

4. Если разрезать кубический метр на кубические сантиметры и поставить их один на другой, то какой высоты получится столб?

При решении этой задачи следует использовать результаты предыдущей задачи.

IV. Итоги урока.

– Сформулируйте определение степени с натуральным показателем.

– Чему равна любая натуральная степень нуля?

– Каков порядок действий при нахождении числового и буквенного выражения, содержащего степень?

– Чему равно значение выражения 0,2⁸ · 5⁸? Как рационально вычислить? Каким правилом необходимо воспользоваться?

Домашнее задание: № 390; № 391; № 394; № 398.

Урок 41
Умножение и деление степеней с одинаковыми основаниями

Цели: вывести правила умножения и деления степеней с одинаковым основанием; дать определение нулевой степени числа, не равного нулю; формировать умение выполнять указанные действия со степенями.

Ход урока

I. Устная работа.

1. Вычислите.

а) 3²; б)

; в) (0,1)³; г)

; д)

; е) (–0,1)⁴; ж)

; з) –(–7)²;

и) –(–2)³; к) 0¹⁶; л) (–1)¹⁸; м) –(–1)²³.

2. Сравните значение двух выражений:

а) (–8,64)²⁰ и 0³⁰; б) (–1)⁷⁶ и (–1)⁷⁰; в)

и (–3,82)¹³; г)

.

II. Проверочная работа.

Вариант 1

1. Найдите значение выражения. а)

– (0,5)²; б) 3000 · (0,2)³ – (–2)⁶; в)

– (–3)³.

2. Вычислите значение выражения х³ – х² при: а) х = 0,3; б) х = –6.

Вариант 2

1. Найдите значение выражения.а)

+ (0,6)²; б) 2000 · (0,3)⁴ – (–2)⁴; в)

– (–4)³.

2. Вычислите значение выражения х² + х³ при:а) х = –0,4; б) х = 10.

III. Объяснение нового материала.

На этом уроке изучаем два важных свойства степени: сложение и умножение степеней с одинаковыми основаниями.

Свойство 1. При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.


по сочетательному свойству умножения

по определению степени с натуральным показателем
= 2⁵ Итак, 2² · 2³ = 2^{2 + 3}	= a^m⁺ⁿ

Свойство 2. При делении степеней с одинаковыми основаниями, основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

5 > 3 3⁵ : 3³ =	m > n, a  0 a^m : aⁿ =
запишем частное в виде дроби

сократим дробь

по определению степени с натуральным показателем
= 3² Итак, 3⁵ : 3³ = 3^{5 – 3}	= a^m^–ⁿ

Замечаем, что a^m : a^m = a^{m – m} = a⁰ = 1.

Определение. Степень числа а, не равного нулю, с нулевым показателем равна единице.

IV. Формирование умений и навыков.

1. № 403.

Решение:

а) x⁵x⁸ = x^{5 + 8} = x¹³; е) yy¹² = y^{1 + 12} = y¹³;

ж) 2⁶2⁴ = 2^{6 + 4} + 2¹⁰; з) 7⁵7 = 7^{5 + 1} = 7⁶.

2. № 405.

Решение:

а) a¹⁵ = a^{6 + 9} = a⁶∙ a⁹; б) a¹⁵ = a^{9 + 6} = a⁹∙ a⁶;

в) a¹⁵ = a^{2 + 13} = a²∙ a¹³; г) a¹⁵ = a^{14 + 1} = a¹⁴∙ a = a ∙ a¹⁴.

3. № 407.

Решение:

Представим число 6 в виде суммы двух натуральных чисел всеми возможными способами:

6 = 1 + 5; 6 = 2 + 4; 6 = 3 + 3.

Значит, a⁶ = a ∙ a⁵; a⁶ = a²∙ a⁴; a⁶ = a³∙ a³.

4. № 409.

Решение:

а) m³m²m⁸ = m^{3 + 2 + 8} = m¹³; в) xx⁴x⁴x = x^{1 + 4 + 4 + 1} = x¹⁰;

д) 7⁸∙ 7∙ 7⁴ = 7^{8 + 1 + 4} = 7¹³; е) 5∙ 5²∙ 5³∙ 5⁵ = 5^{1 + 2 + 3 + 4} = 5¹¹.

5. № 410.

Решение:

а) 5⁸ ∙ 25 = 5⁸ ∙ 5² = 5^{8 + 2} = 5¹⁰;

в) 6¹⁵ ∙ 36 = 6¹⁵ ∙ 6² = 6^{15 + 2} = 6¹⁷;

д) 0,4⁵ ∙ 0,16 = 0,4⁵ ∙ 0,4² = 0,4^{5 + 2} = 0,4⁷;

е) 0,001 ∙ 0,1⁴ = 0,1³ ∙ 0,1⁴ = 0,1^{3 + 4} = 0,1⁷.

6. № 411.

Решение:

а) 2⁴ ∙ 2 = 2^{4 + 1} = 2⁵ = 32;

б) 2⁶ ∙ 4 = 2⁶ ∙ 2² = 2^{6 + 2} = 2⁸ = 256;

в) 8 ∙ 2⁷ = 2³ ∙ 2⁷ = 2^{3 + 7} = 2¹⁰ = 1024;

г) 16 ∙ 32 = 2⁴ ∙ 2⁵ = 2^{4 + 5} = 2⁹ = 512.

7. № 413.

Решение:

а) (c⁴)² = c⁴ ∙ c⁴ = c^{4 + 4} = c⁸;

б) (c²)⁴ = c² ∙ c² ∙ c² ∙ c² = c^{2 + 2 + 2 + 2} = c⁸.

V. Итоги урока.

Домашнее задание: № 404; № 406; № 408; 412; № 533.

Вариант 1

1. Найдите значение выражения. а)

– (0,5)²; б) 3000 · (0,2)³ – (–2)⁶; в)

+ (0,6)²; б) 2000 · (0,3)⁴ – (–2)⁴; в)

– (–4)³.

2. Вычислите значение выражения х² + х³ при:а) х = –0,4; б) х = 10.
Вариант 1

1. Найдите значение выражения. а)

– (0,5)²; б) 3000 · (0,2)³ – (–2)⁶; в)

+ (0,6)²; б) 2000 · (0,3)⁴ – (–2)⁴; в)

– (0,5)²; б) 3000 · (0,2)³ – (–2)⁶; в)

+ (0,6)²; б) 2000 · (0,3)⁴ – (–2)⁴; в)

– (–4)³.

2. Вычислите значение выражения х² + х³ при:а) х = –0,4; б) х = 10.
Вариант 1

Карточка 1

1. Найдите значение выражения. а)

– (0,5)²; б) 3000 · (0,2)³ – (–2)⁶; в)

– (–3)³.

2. Вычислите значение выражения х³ – х² при: а) х = 0,3; б) х = –6.

Карточка 2

1. Найдите значение выражения.а)

+ (0,6)²; б) 2000 · (0,3)⁴ – (–2)⁴; в)

– (–4)³.

2. Вычислите значение выражения х² + х³ при:а) х = –0,4; б) х = 10.

Карточка 1

1. Найдите значение выражения. а)

– (0,5)²; б) 3000 · (0,2)³ – (–2)⁶; в)

+ (0,6)²; б) 2000 · (0,3)⁴ – (–2)⁴; в)

– (0,5)²; б) 3000 · (0,2)³ – (–2)⁶; в)

+ (0,6)²; б) 2000 · (0,3)⁴ – (–2)⁴; в)

– (0,5)²; б) 3000 · (0,2)³ – (–2)⁶; в)

+ (0,6)²; б) 2000 · (0,3)⁴ – (–2)⁴; в)

– (0,5)²; б) 3000 · (0,2)³ – (–2)⁶; в)

+ (0,6)²; б) 2000 · (0,3)⁴ – (–2)⁴; в)

– (–4)³.

2. Вычислите значение выражения х² + х³ при:а) х = –0,4; б) х = 10.

Предмет: Алгебра

Класс: 7

1 ... 7 8 9 10 11 12 13 14 ... 22