Урок 1 Числовые выражения

• Название: Урок 1 Числовые выражения
• Дата: 09.03.2021
• Размер: 1.93 Mb.
• Имя файла: 1-63.doc
• Тип: Урок; #183094
• страница: 13 из 22

Тема: Возведение в степень произведения и степени

Дата: 15.11.19 г

Цели: вывести правило возведения в степень произведения двух и более сомножителей; формировать умение вычислять степень произведения, а также рационально преобразовывать выражения, содержащие степень произведения либо предполагающие использование данного свойства.

Ход урока

I. Организационный момент

Устная работа.

Вычислите.

а) 2³ · 5³; в) 12²;

б) 10³; г) 3² · 4²;

II. Объяснение нового материала.

(ab)n = anbn.
Для любых а и b и произвольного натурального п верно равенство (ab)n = anbn.

Доказательство:

(ab)ⁿ = (ab) · (ab) · ... · (ab) по определению степени п раз;

(ab) · (ab) · ... · (ab) = (aa...a)(bb...b) по свойствам умножения п раз п раз; (ab)ⁿ = aⁿbⁿ.

Вывод:

1) каждый множитель возводить в эту степень;

2) результаты перемножить.

Пример:

(abсd)⁴ = ...

Решение:

(abcd)⁴ = a⁴b⁴c⁴d⁴.

Рассмотреть пример 1 со с. 97 учебника.

III. Формирование умений и навыков.

1. № 428.

2. Выполните возведение в степень, представив предварительно основание степени в виде произведения множителей –1 и х:

а) (–х)²; б) (–х)⁸; в) (–х)¹⁰⁰; г) (–х)^2п;

д) (–х)³; е) (–х)⁹; ж) (–х)⁷¹; з) (–х)^{2п + 1}.

Решение:

а) (–х)² = ((–1) · х)² = (–1)² · х² = 1 · х² = х²;

е) (–х)⁹ = ((–1) · х)⁹ = (–1)⁹ · х⁹ = –1 · х⁹ = –х⁹;

г) (–х)^2п = ((–1) · х)^2п = (–1)^2п · х^2п = 1 · х^2п = х^2п;

з) (–х)^{2п + 1} = ((–1) · х)^{2п + 1} = (–1)^{2п + 1} · х^{2п + 1} = –1 · х^{2п + 1} = –х^{2п + 1}.

3. № 431.

Решение:

а и –а – противоположные числа.

а²;

(–а)² = ((–1) · а)² = (–1)² · а² = 1 · а² = а²,

значит, а² = (–а²).

4. № 432.

Решение:

Пусть а – сторона квадрата, тогда площадь квадрата равна а2. Если сторона квадрата увеличится в 2 раза, то станет равна 2а, а его площадь будет равна (2а) · (2а) = = (2а)2 = 22 · а2 = 4а2, то есть увеличится в 4 раза.

Аналогично рассуждаем для остальных случаев.

5. № 433.

Решение:

Пусть а – ребро куба, тогда его объем равен а3. Если ребро увеличить в 3 раза, то объем куба будет вычисляться по формуле (3а) · (3а) · (3а) = (3а)3 = = 33 · а3 = 27а3, значит, объем увеличится в 27 раз.

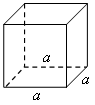
6. № 434.

Для решения используем данные задачи № 432.

Решение:

Поверхность куба состоит из 6 квадратов площадью а², то есть равна 6а².

Если ребро куба увеличить в 3 раза, то площадь боковой грани составит 9а², а общая площадь поверхности равна 6 · 9а² или 54а².

Новая площадь больше в 9 раз, значит, и краски потребуется в 9 раз больше, то есть 40 · 9 = 360 г. Следовательно, 350 г краски на хватит.

Ответ: не хватит.

7. Представьте произведение в виде степени.

а) x⁵y⁵; б) 36a²b²; в) 0,001x³c³;

г) –х³; д) –8х³; е) –32a⁵b⁵;

ж) x⁵y⁵z⁵; з) 0,027a³b³c³; и) x³a³z³.

8. Вычислите значение выражения, используя свойство степени произведения.

а) 5³ · 2³; в) (0,5)³ · 60³;

б) · 20⁴; г) (1,2)⁴ · .

IV. Итоги урока.

– Сформулируйте определение степени с натуральным показателем.

– Сформулируйте правило возведения в степень произведения.

– Сколько сомножителей может стоять в формуле степени произведения?

– Чему равно значение выражения (3 · 5 · 78)⁰?

Домашнее задание: № 429; № 430; № 435; № 436; № 437.

Предмет: Алгебра

Класс: 7

Тема: Возведение в степень произведения и степени

Дата: 19.11.19 г

Цели: вывести правило возведения степени в степень; формировать умение выполнять преобразование выражений, содержащих степень в степени.

Ход урока

I. Проверочная работа.

Вариант 1

1. Возведите в степень произведение. а) (xyz)⁸; б) ; в) (–2а)³; г) .

2. Вычислите значение выражения. а) 25² · 4²; б) · 9³; в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение. а) (abc)¹⁰; б) ; в) (–4а)³; г) .

2. Вычислите значение выражения. а) 20³ · 5³; б) · 25²; в) (–0,2)⁴ · 50⁴.

II. Объяснение нового материала.

1. Устная работа.

Представьте в виде степени.

а) (а⁵)³ = а⁵ · а⁵ · а⁵ = … ; б) (у²)⁵ = … ;

в) (а^т)⁷ = … ; г) (а^т)^п = … .

В результате появится запись:

(ат)п = ат п.

2. Доказательство свойства можно оформить в виде таблицы.

Свойство. При возведении степени в степень основание оставляют тем же, а показатели перемножают.

(23)2 = 23 · 23 =
по первому свойству степени
= 23 + 3 =
по определению умножения
= 23 · 2 Итак, (23)2 = 23 · 2	= am · n

Подчеркиваем, что формулу можно применять в следующем виде:

(am)n = am n = an m = (an)m.

III. Формирование умений и навыков.

1. № 438 (устно).

Решение:

а) (х³)² = х^{3 · 2} = х⁶;

з) (b⁵)² = b^{5 · 2} = b¹⁰.

2. № 440, № 441.

№ 441.

Решение:

а) а^п · а³ = а^{п + 3};

г) (а²)^т = а^2т.

3. № 443, № 445, № 446.

№ 443.

Решение:

а) 2²⁰ = 2^{2 · 10} = (2²)¹⁰; б) 2²⁰ = 2^{4 · 5} = (2⁴)⁵;

в) 2²⁰ = 2^{5 · 4} = (2⁵)⁴; г) 2²⁰ = 2^{10 · 2} = (2¹⁰)².

№ 445.

Решение:

12 = 1 · 12; а¹² = (а¹)¹²;

12 = 2 · 6; а¹² = (а²)⁶;

12 = 3 · 4; а¹² = (а³)⁴;

12 = 4 · 3; а¹² = (а⁴)³;

12 = 6 · 2; а¹² = (а⁶)²;

12 = 12 · 1; а¹² = (а¹²)¹.

№ 446. Решение:

а² = т;

а⁶ = а^{2 · 3} = (а²)³ = т³.

4. Представьте выражение в виде квадрата числа.

а) а⁴; б) b⁶; в) d⁸; г) c¹⁰;

д) d²⁰; е) ; ж) 1 ; з) .

5. № 447, № 449 (а, б), № 450 (а, б).

№ 447.

Решение:

а) x³ · (x²)⁵ = x³· x^{2 · 5}= x³· x¹⁰= x^{3 + 10}= x¹³;

б) (a³)² · a⁵ = a^{3 · 2} · a⁵ = a⁶ · a⁵ = a^{6 + 5} = a¹¹;

в) (a²)³ · (a⁴)² = a^{2 · 3} · a^{4 · 2} = a⁶ · a⁸ = a^{6 + 8} = a¹⁴;

г) (x²)⁵ · (x⁵)² = x^{2 · 5}· x^{5 · 2}= x¹⁰· x¹⁰= (x¹⁰)²= x^{10 · 2}= x²⁰;

д) (a³a³)² = (a⁶)² = a^{6 · 2} = a¹²;

е) (aa⁶)³ = a³ · (a⁶)³ = a³· a^{6 · 3} = a³· a¹⁸ = a^{3 + 18} = a²¹.

№ 449.

Решение:

а) x⁵ · (x²)³ = x⁵· x⁶= x¹¹;

б) (x³)⁴· x⁸ = x¹²· x⁸= x²⁰.

IV. Итоги урока.

– Сформулируйте определение степени с натуральным показателем.

– Сформулируйте правило возведения степени в степень. приведите примеры.

– Каков алгоритм возведения степени в степень?

– Чему равно значение выражения: ; (x³)⁰?

Домашнее задание: № 439; № 442; № 444.

Вариант 1

1. Возведите в степень произведение. а) (xyz)⁸; б) ; в) (–2а)³; г) .

2. Вычислите значение выражения. а) 25² · 4²; б) · 9³; в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение. а) (abc)¹⁰; б) ; в) (–4а)³; г) .

2. Вычислите значение выражения. а) 20³ · 5³; б) · 25²; в) (–0,2)⁴ · 50⁴.

Вариант 1

1. Возведите в степень произведение. а) (xyz)⁸; б) ; в) (–2а)³; г) .

2. Вычислите значение выражения. а) 25² · 4²; б) · 9³; в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение. а) (abc)¹⁰; б) ; в) (–4а)³; г) .

2. Вычислите значение выражения. а) 20³ · 5³; б) · 25²; в) (–0,2)⁴ · 50⁴.

Вариант 1

1. Возведите в степень произведение. а) (xyz)⁸; б) ; в) (–2а)³; г) .

2. Вычислите значение выражения. а) 25² · 4²; б) · 9³; в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение. а) (abc)¹⁰; б) ; в) (–4а)³; г) .

2. Вычислите значение выражения. а) 20³ · 5³; б) · 25²; в) (–0,2)⁴ · 50⁴.

Вариант 1

1. Возведите в степень произведение. а) (xyz)⁸; б) ; в) (–2а)³; г) .

2. Вычислите значение выражения. а) 25² · 4²; б) · 9³; в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение. а) (abc)¹⁰; б) ; в) (–4а)³; г) .

2. Вычислите значение выражения. а) 20³ · 5³; б) · 25²; в) (–0,2)⁴ · 50⁴.

Вариант 1

1. Возведите в степень произведение. а) (xyz)⁸; б) ; в) (–2а)³; г) .

2. Вычислите значение выражения. а) 25² · 4²; б) · 9³; в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение. а) (abc)¹⁰; б) ; в) (–4а)³; г) .

2. Вычислите значение выражения. а) 20³ · 5³; б) · 25²; в) (–0,2)⁴ · 50⁴.

Урок 46