Урок 1 Числовые выражения

Название	Урок 1 Числовые выражения
Дата	09.03.2021
Размер	1.93 Mb.
Формат файла
Имя файла	1-63.doc
Тип	Урок #183094
страница	20 из 22

1 ... 14 15 16 17 18 19 20 21 22

сложение и вычитание многочленов

Цели: продолжить формирование умения выполнять сложение и вычитание многочленов.

Ход урока

I. Устная работа.

Выполните сложение или вычитание многочленов.

а) (1 + a) + (3 + 2a); г) (5 – y) + (3y – 2);

б) (a – b) – (a + b); д) 4p² – (p² + 2);

в) 3x – (1 – 2x); е) (2 + x) – (x – 3).

II. Формирование умений и навыков.

1. № 590, № 592.

2. № 593.

Решение:

M + (5x² – 2xy) = 6x² + 9xy – y².

Слева: Справа:

5х² 6х²

–2ху 9ху

0 –у²

Нужно найти такие одночлены, которые в сумме с одночленами из левой части дадут одночлены, равные стоящим в правой части. Получаем их: х², 11ху, у².

Значит, вместо М нужно записать многочлен х² + 11ху + у².

б) M – (4ab – 3b²) = a² – 7ab + 8b².

Сначала раскроем скобки: М – 4ab + 3b² = a² – 7ab + 8b².

Слева: Справа:

–4ab –7ab

3b² 8b²

0 a²

Находим недостающие одночлены: –3ab, 5b², –а². Получаем многочлен: 5b² – 3ab – а².

Если задание не вызывает затруднений у учащихся, то они могут выполнять его устно.

3. Запишите во втором столбце многочлен, сумма которого с многочленом из первого столбца равна многочлену из третьего столбца.

1) 3х + 5

2) 7х + 3

3) a³ + 3a²b + b³

4) 2x²y – 3xy² – 8

5) x² + 2xy + y²

6) 3x + 2a

8х – 11

х² + 7х – 15

a³ + 3a²b + b³

0

x² – 2xy + y²

2x + b

4. № 605.

Решение:

Необходимо объяснить учащимся, что решение любого уравнения начинается с его преобразования.

в) (3,2у – 1,8) – (5,2у + 3,4) = –5,8;

3,2у – 1,8 – 5,2у – 3,4 = –5,8;

3,2у – 5,2у = 1,8 + 3,4 – 5,8;

–2у = –0,6;

у = –0,6 : (–2);

у = 0,3.

Ответ: 0,3.

д) 3,8 – 1,5у + (4,5у – 0,8) = 2,4у + 3;

3,8 – 1,5у + 4,5у – 0,8 = 2,4у + 3;

– 1,5у + 4,5у – 2,4у = 3 – 3,8 + 0,8;

0,6у = 0;

у = 0.

Ответ: 0.

III. Итоги урока.

– Что называется многочленом? степенью многочлена?

– Как раскрыть скобки, перед которыми стоит знак «+»? знак «–»?

– Как выполнить сложение или вычитание многочленов?

Домашнее задание: № 594; № 596; № 606.

1.     Приведите подобные члены многочлена:

а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t

2. Раскройте скобки и приведите подобные слагаемые:

а) (12а + 3 b) + (7а - 4 b);   б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)

3. Докажите, что при любом значении х значение выражения

(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1.     Приведите подобные члены многочлена:

а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t

2. Раскройте скобки и приведите подобные слагаемые:

а) (12а + 3 b) + (7а - 4 b);   б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)

3. Докажите, что при любом значении х значение выражения

(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1.     Приведите подобные члены многочлена:

а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t

2. Раскройте скобки и приведите подобные слагаемые:

а) (12а + 3 b) + (7а - 4 b);   б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)

3. Докажите, что при любом значении х значение выражения

(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1.     Приведите подобные члены многочлена:

а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t

2. Раскройте скобки и приведите подобные слагаемые:

а) (12а + 3 b) + (7а - 4 b);   б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)

3. Докажите, что при любом значении х значение выражения

(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1.     Приведите подобные члены многочлена:

а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t

2. Раскройте скобки и приведите подобные слагаемые:

а) (12а + 3 b) + (7а - 4 b);   б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)

3. Докажите, что при любом значении х значение выражения

(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.
1.     Приведите подобные члены многочлена:

а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t

2. Раскройте скобки и приведите подобные слагаемые:

а) (12а + 3 b) + (7а - 4 b);   б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)

3. Докажите, что при любом значении х значение выражения

(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.

1.     Приведите подобные члены многочлена:

а) 5х + 6у – 3х – 12у b) 3t² - 5t + 11 - 3t² + 5t

2. Раскройте скобки и приведите подобные слагаемые:

а) (12а + 3 b) + (7а - 4 b);   б) (4ху – 6х²) – (-ху + 5х²); в) (а² + 2а -1) + (3а² - а + 6)

3. Докажите, что при любом значении х значение выражения

(2,6х + 5) + (4,1х – 1) – (6,7х + 2) равно 2.

умножение одночлена на многочлен

Цели: изучить правило умножения одночлена на многочлен; формировать умение применять это правило при преобразовании выражений.

Ход урока

I. Устная работа.

Упростите выражение.

а) а⁵ · а⁷; в) аа²а³; д) (п³)² п⁴;

б) х⁸ : х³; г) (х²)⁵; е) у² у³(у⁴)².

II. Объяснение нового материала.

При объяснении этого материала достаточно привести несколько примеров умножения одночлена на многочлен и сформулировать соответствующее правило.
III. Формирование умений и навыков.

1. № 614; № 615 (а, в, д).

2. № 616.

Решение:

(На первых порах желательно, чтобы учащиеся (особенно слабые) вели подробные записи, это позволит избежать ошибок в преобразованиях.)

в)

г)

Физминутка

3. № 618 (а, в).

Решение:

(Здесь важно ещё раз напомнить учащимся о том, что перед нахождением значения любого выражения его сначала упрощают.)

в) 4у – 2 (10у – 1) + (8у – 24) = 4у – 20у + 2 + 8у – 24 = –8у – 22

при у = –0,1: –8у – 22 = –8 · (–0,1) – 22 = 0,8 – 22 = –21,2.

4. № 619.

IV. Рефлексия.

– Как выполнить умножение одночлена на одночлен?

– Перемножьте одночлены –2х² и 5х⁴.

– Сформулируйте правило умножения одночлена на многочлен.

– Умножьте одночлен 4а³ на многочлен 2а – 3.

Домашнее задание: № 617; 618 (б, г); № 620.

Урок 59 Умножение одночлена на многочлен

Цели: продолжить формирование умения умножать одночлен на многочлен; формировать умение выполнять данное действие при решении уравнений.

Ход урока

I. Устная работа.

1. Выполните умножение одночленов.

а) 2х⁵ · 3х²; в) (–3b) · (–7b); д) (х²)³ · 5х;

б) –4a³ ·

a; г)

y⁷ · (–3y); е)

.

2. Упростите выражение.

а) 2x (x² – 4x); в) 4y ;

б) –а² (а + 8); г)

p²(2p – 4).

II. Формирование умений и навыков.

1. № 630 (а, в, д, ж).

2. № 631 (а, в).

Решение:

а) 3х (2х – 1) – 6х (7 + х) = 90;

6х² – 3х – 42х – 6х² = 90;

–45х = 90;

х =

;

х = –2.

Ответ: –2.

в) 5x (12x – 7) – 4x (15x – 11) = 30 + 29x;

60x² – 35x – 60x² + 44x = 30 + 29x;

–35х + 44 х – 29х = 30;

–20х = 30;

х =

;

х = –1,5.

Ответ: –1,5.

1. № 634 (а, в, д, и).

2. № 636.

3. № 637.

Решение:

б)

.

Умножим обе части уравнения на 30:

;

3 (a + 13) – 6 · 2a = 2 (3 – a) + 15a;

3а + 39 – 12а = 6 – 2а + 15а;

–9а – 13а = 6 – 39;

–22а = –33;

а =

;

а = 1,5.

Ответ: 1,5.

г)

.

Умножим обе части уравнения на 18:

;

2 (х + 1) – 3 (х – 1) = 36 – 9 (х + 3);

2х + 2 – 3х + 3 = 36 – 9х – 27;

–х + 9х = 9 – 5;

8х = 4;

х =

.

Ответ: 0,5.

1. № 622.

2. № 629.

Решение:

Преобразуем данное выражение:

2x (x – 6) – 3 (x² – 4x + 1) = 2x² – 12x – 3x² + 12x – 3 = – x² – 3.

Очевидно, что при любом значении х значение выражения –х² будет неположительным, тогда значение выражения –х² – 3 будет отрицательным при любом значении х.

III. Итоги урока.

– Как выполнить умножение одночлена на одночлен?

– Сформулируйте правило умножения одночлена на многочлен.

– Как решить уравнение, в котором встречаются дроби?

Домашнее задание: № 632; № 634 (б, г, е, з); № 638; № 627.

Урок 60 Умножение одночлена на многочлен

Цели: формировать умение решать задачи с помощью уравнений; закрепить умение выполнять умножение одночлена на многочлен; проверить степень усвоения учащимися изученного материала.

Ход урока

I. Устная работа.

1. Выполните умножение одночленов.

а) 3а² · (–2а); г)

x⁶ · (–4x); б) 7b³ ·

b²; д) (а²)⁴ · 2а; в) –4с · (–2с⁵); е)

.

2. Упростите выражение.

а) 3а (4 – а²); в) 2n

; б) –х³ (х + 2); г)

y²(5 + 2y).

II. Проверочная работа.

Вариант 1

1. Упростите выражение.а) 3p (8c + 1) – 8c (3p – 5); б) 5n² (3n + 1) – 2n (5n² – 3).

2. Решите уравнение.а) 6x – 5 (3x + 2) = 5 (x – 1) – 8; б)

= 2.

3. Преобразуйте в многочлен стандартного вида:–xt (x²t² – xt – 3) · p.

Вариант 2

1. Упростите выражение.а) 5b (3a – b) – 3a (5b + a); б) a (2a² – 3n) – n (2n² + a).

2. Решите уравнение.а) 40 – 8 (11 – 2x) = 3 (5x – 4); б)

.

3. Преобразуйте в многочлен стандартного вида:–ab (a²b – ab² – a³b³) · p.

III. Формирование умений и навыков.

1. № 642.

Решение:

Составим таблицу:

	Было	Стало
1-й сарай	3х т	(3х – 2) т
2-й сарай	х т	(х + 2) т

Составим и решим уравнение.

x + 2 =

(3x – 2);

7 (х + 2) = 5 (3х – 2);

7х + 14 = 15х – 10;

–8х = –24;

х = 3.

Значит, во втором сарае было 3 т сена, а в первом 9 т сена.

Ответ: 9 т, 3 т.

2. № 643.

Решение:

Составим таблицу:

	А	k	t
По плану	х га	50 га/день	дн.
Реально	х га	60 га/день	дн.

Составим и решим уравнение:

= 1;

300

= 300;

6х – 5х = 300;

х = 300.

Значит, площадь луга равна 300 га.

Ответ: 300 га.

3. № 646.

Решение:

Составим таблицу:

	s	υ	t
Велосипедист	х км	12 км/ч	ч
Мотоциклист	(х + 60) км	30 км/ч	ч

Составим и решим уравнение:

;

;

5х = 2 (х + 60);

5х = 2х + 120;

3х = 120;

х = 40.

Значит, велосипедист проехал 40 км до того, как его догнал мотоциклист.

Ответ: 40 км.

4. № 648.

Решение:

Представим наглядно описанную в задаче ситуацию.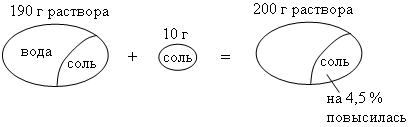

Пусть первоначально в растворе было х г соли, то есть её концентрация была равна

∙ 100 % =

%.

В новом растворе уже имеется (х + 10) г соли, значит, её концентрация стала равна

∙ 100 % =

%. По условию концентрация соли в новом растворе повысилась на 4,5 %.

Составим и решим уравнение:

= 4,5;

19(х + 10) – 20х = 38 · 4,5;

19х + 190 – 20х = 171;

–х = –19;

х = 19.

Ответ: 19 г.

1 ... 14 15 16 17 18 19 20 21 22