планы 6 класс. ПОУРОЧКА_6_КЛ_ФГОС. Урок 2 Наибольший общий делитель. Взаимно простые числа

• Название: Урок 2 Наибольший общий делитель. Взаимно простые числа
• Анкор: планы 6 класс
• Дата: 20.04.2022
• Размер: 2.52 Mb.
• Имя файла: ПОУРОЧКА_6_КЛ_ФГОС.doc
• Тип: Урок; #486297
• страница: 29 из 34

III. Изучение нового материала.

1. Распределительное свойство умножения (а + в) · с = ас + вс справедливо для любых чисел а, в, с.

Замену выражения (а + в) · с выражением ав + ас или выражения с · (а + в) выражением са + св также называют раскрытием скобок.

2. Разобрать решение примеров 1 и 2 на с. 224 учебника.

3. Определение подобных слагаемых.

Подобные слагаемые могут отличаться только коэффициентами.

Примеры: а) 11а – 5а + 7а – 9а = 4а;

б) 7у + 8у – у + 5у = 19у; в) – 6в – 10в + 3в = – 13в.

4. Сформулировать правило сложения (или говорят: приведения) подобных слагаемых. Разобрать решение примера

IV. Закрепление нового материала.

1. Решить № 393 (а; б; г) устно; № 393 (е; ж; з) – на доске и в тетрадях.

2. Решить № 392 (а; б; д; е) с комментированием на месте.

Решение.

а) (а – в + с) · 8 = 8а – 8в + 8с; б) – 5 · (m – п –к) = – 5m + 5п + 5к;

д) (3m – 2к + 1) · (– 3) = – 9m + 6к –3;

е) – 2а · (в + 2с – 3m) = – 2ав – 4ас + 6 аm.

3. Решить № 394 (а; б; д; е; ж) на доске и в тетрадях.

Решение.

а) – 9х + 7х – 5х + 2х = – 5х; б) 5а – 6а + 2а – 10а = – 9а;

д) а + 6,2а – 6,5а – а = – 0,3 а;

е) – 18п – 12п + 7,3п + 6,5п = – 30п + 13,8п = – 16,2п;

ж) .

4. Решить № 395 (а; б; е; ж) (объясняет решение учитель).

Решение.

а) 10а + в – 10в – а = 9а – 9в;

б) – 8у + 7х + 6у +7х = 14х – 2у;

е) – 6а + 5а – х +4 = – а – х +4;

ж) 23х – 23 + 40 + 4х = 27х +17.

5. Повторение ранее изученного материала.

1) Решить задачу № 409

Решение.

440 000 000 : 88 = 5 000 000.

Масштаб 1 : 5 000 000.

2) Решить задачу № 411 самостоятельно.

3) Решить задачу № 412 (1) на доске и в тетрадях.

Решение.

100 % + 15 % = 115 % выполнен план;

115 % = 1,15.

230 : 1,15 = 23 000 : 115 = 200 (га) по плану.

Ответ: 200 га.

V. Итог урока.

1. Ответить на вопросы к пункту

2. Приведите подобные слагаемые:

а) 8m + 14п –9m –15п + 7п; б) 3х + 15у – 2х – 20у + 7х.

Домашнее задание: изучить п. 41; решить № 415 (а; б), № 416 (а; б; г), № 417 (а – г), № 422

Урок 2 Подобные слагаемые

Цели: способствовать выработке навыков и умений при приведении подобных слагаемых, решении примеров и задач; закреплять изученный материал; развивать логическое мышление учащихся, воспитание математической речевой культуры, гигиеническое воспитание и формирование здорового образа жизни в целях сохранения психического, физического и нравственного здоровья человека, развитие интеграционных связей с другими дисциплинами, проведение анализа межпредметных связей, опора на морально-нравственные ценностные ориентиры, увеличение развивающих способностей, развитие нестандартного мышления, использование личностного и субъектного опыта.
Планируемые результаты
Предметные: Научиться рас­крывать скобки и приводить подобные слагае­мые, основываясь на свойствах дей­ствий с рациональными числами
Метапридметные: Коммуникативные: развивать умение точно и грамотно выражать свои мысли, отстаивать свою точку зрения в процессе дискуссии. Регулятивные: определять последователь­ность промежуточных действий с учетом ко­нечного результата, составлять план. Познавательные: уметь осуществлять анализ объектов с выделением существенных и несу­щественных признаков
Личностные: формировать устойчивую мотивацию к обучению на основе алго­ритма выпол­нения заданий
Основные понятия: Подобные слагаемые
Ход урока

Орг. момент

Определение темы и цели урока

I. Актуализация опорных знаний учащихся.

1. Учитель выборочно проверяет домашнее задание учащихся по тетрадям.

2. Какие слагаемые называют подобными? Как привести подобные слагаемые? Пояснить на примерах.

3. Решить № 401

5. Решить № 405 (а; б), записывая решение только на доске.

II. Тренировочные упражнения.

1. Решить № 393 (в; д; и) самостоятельно с проверкой.

2. Решить № 392 (ж; з) на доске, № 1265 (в; г) – самостоятельно.

3. Решить № 394 (в; г; з; и) на доске и в тетрадях.

Решение.

в) 11р + 2р + 20р –7р = 26р;

г) – 3,8к – к + 3,8к + к = 0;

з) ;

и) .

4. Решить №396 (г – з) на доске и в тетрадях, № 396 (а; б; в) – самостоятельно.

Решение.

а) 7 · (2х – 3) + 4 · (3х – 2) = 14х – 21 + 12х – 8 = 26х – 29;

б) – 2 ·(4к + 8) – 3 · (5к – 1) = – 8к – 16 – 15к + 3 = – 23к –13;

в) – 8 (2 – 2у) + 4 · (3 – 4у) = -16 + 16у +12 – 16у = – 4;

г) (3х – 11) · 2 – 5 · (4 – 3х) = 6х – 22 –20 + 15х = 21х – 42;

д) (8а – 1) · (– 6) + (3а – 7) · (– 2) = – 48а + 6 – 6а +14 = 20 –54а;

е) – 0,5 · (– 2х + 4) – (10 – х) = х – 2 – 10 + х = 2х – 12;

ж) – 6 · ;

з) 5 · .

5. Решить уравнение № 398(а; в) на доске и в тетрадях.

Решение.

а) в)





х = – 22. х = 49 – 9

Ответ: х = – 22. х = 40.

Ответ: х = 40.

6. Повторение ранее изученного материала.

1) Решить задачу № 409самостоятельно.

2) Решить задачу № 410 с комментированием на месте.

3) Сравните с нулем:

а) (– 0,3)²; б) (– 4,8)³; в) (– 1,05)⁴; г) ; д) (– 1)¹¹;

е) .

III. Итог урока.

1. Приведите подобные слагаемые:

2. Упростите выражение

.

3. Найдите корень уравнения

3 · (0,4х + 7) – 4 · (0,8х – 3) = 2.

Домашнее задание: решить № 415 (в; г), № 416 (в; д; е), № 417 (в; г; к; л), № 418 (а; б; д; е), № 424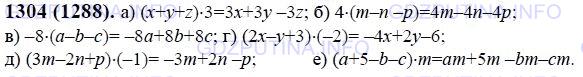










Урок 3 Подобные слагаемые

Цели: закрепить изученный материал в ходе выполнения упражнений; проверить его усвоение при выполнении самостоятельной работы, воспитание математической речевой культуры, гигиеническое воспитание и формирование здорового образа жизни в целях сохранения психического, физического и нравственного здоровья человека, развитие интеграционных связей с другими дисциплинами, проведение анализа межпредметных связей, опора на морально-нравственные ценностные ориентиры, увеличение развивающих способностей, развитие нестандартного мышления, использование личностного и субъектного опыта.
Планируемые результаты
Предметные: Совершенство­вать навык приве­дения подобных слагаемых и на­учиться приме­нять его при ре­шении уравнений и текстовых задач
Метапридметные: Коммуникативные: развивать умение точно и грамотно выражать свои мысли, отстаивать свою точку зрения в процессе дискуссии. Регулятивные: определять последователь­ность промежуточных действий с учетом ко­нечного результата, составлять план. Познавательные: уметь осуществлять анализ объектов с выделением существенных и несу­щественных признаков
Личностные: формировать устойчивую мотивацию к обучению на основе алго­ритма выпол­нения заданий
Основные понятия: Подобные слагаемые
Ход урока

Орг. момент

Определение темы и цели урока

I. Устная работа.

1. Повторить правила и свойства умножения рациональных чисел. Привести свои примеры. Распределительное свойство умножения относительно сложения и вычитания.

2. Решить № 406

II. Тренировочные упражнения.

1. Повторить определение подобных слагаемых и правило приведения подобных слагаемых. Привести свои примеры.

2. Решить № 392 (в; г; з) с комментированием на месте, № 392 (д; и; к) на доске и в тетрадях.

Решение.

д)

;

и) – 12р + 3к + 3,2р – 2,3к = 0,7к – 8,8р;

к) .

3. Решить № 397 (б) на доске и в тетрадях, № 397(а) – самостоятельно.

Решение.

а) 4х – 2а + 6х – 3а + 4а = 10х – а = 10 · (– 0,15) – 0,03 =

= – 1,5 – 0,03 = – 1,53;

б) – 6,3m + 8 – 3,2m – 5 = – 9,5m + 3 = – 9,5 · (– 2) + 3 = 19 + 3 = 22.

4. Решить № 398 (б) на доске и в тетрадях.

Решение.

б) – 3 · (3у + 4) + 4 · (2у –1) = 0

– 9у – 12 + 8у – 4 = 0

– у –16 = 0

– у = 16

у = – 16.

Ответ: у = – 16.

5. Решить задачу № 399

Решение.

Пусть в столовую привезли х мешков капусты, тогда картофеля привезли (х + 3) мешка. Всего привезли 1,62 ц = 162 кг картофеля и капусты.

20 · (х + 3) + 14х = 162

20х + 60 + 14х = 162

34х + 60 = 162

34х = 102

х = 102 : 34

х = 3.

Привезли 3 мешка капусты и 6 мешков картофеля.

Ответ: 6 мешков и 3 мешка.

6. Решить задачу № 400

7. Повторение ранее изученного материала:

1) Решить задачу № 408 самостоятельно.

2) Решить задачу № 412 (2) с комментированием на месте.

Решение.

100 % – 16 % = 84 % досок израсходовала на ремонт бригада плотников;

4,2 : 0,84 = 420 : 84 = 5 (м³) досок было выделено бригаде на ремонт здания.

Ответ: 5 м³.

III. Самостоятельная работа.

Вариант I.

1. Упростите выражение:

а) – 4с · 3d; б) – 0,2а · (– 3,1в); в) .

2. Приведите подобные слагаемые: .

3. Упростите выражение: .

4. Найдите значение выражения: 5(4а – 3в) – 2(5а – 3в), если

а = – 0,3; в = 0,7.

5. Решите уравнение: .

Вариант II.

1. Упростите выражение:

а) – 8а · (– 5в); б) 0,5х · (– 2,4у); в) .

2. Приведите подобные слагаемые: .

3. Упростите выражение: .

4. Найдите значение выражения: 3 (5m – 4п) – 4 (3m – 2п), если

m = – 0,2; п = 0,7.

Итог урока

Дом. задание


Вариант I.

1. Упростите выражение:

а) – 4с · 3d; б) – 0,2а · (– 3,1в); в) .

2. Приведите подобные слагаемые: .

3. Упростите выражение: .

4. Найдите значение выражения: 5(4а – 3в) – 2(5а – 3в), если

а = – 0,3; в = 0,7.

5. Решите уравнение: .

Вариант II.

1. Упростите выражение:

а) – 8а · (– 5в); б) 0,5х · (– 2,4у); в) .

2. Приведите подобные слагаемые: .

3. Упростите выражение: .

4. Найдите значение выражения: 3 (5m – 4п) – 4 (3m – 2п), если

m = – 0,2; п = 0,7.

Вариант I.

1. Упростите выражение:

а) – 4с · 3d; б) – 0,2а · (– 3,1в); в) .

2. Приведите подобные слагаемые: .

3. Упростите выражение: .

4. Найдите значение выражения: 5(4а – 3в) – 2(5а – 3в), если

а = – 0,3; в = 0,7.

5. Решите уравнение: .

Вариант II.

1. Упростите выражение:

а) – 8а · (– 5в); б) 0,5х · (– 2,4у); в) .

2. Приведите подобные слагаемые: .

3. Упростите выражение: .

4. Найдите значение выражения: 3 (5m – 4п) – 4 (3m – 2п), если

m = – 0,2; п = 0,7.


Вариант I.

1. Упростите выражение:

а) – 4с · 3d; б) – 0,2а · (– 3,1в); в) .

2. Приведите подобные слагаемые: .

3. Упростите выражение: .

4. Найдите значение выражения: 5(4а – 3в) – 2(5а – 3в), если

а = – 0,3; в = 0,7.

5. Решите уравнение: .

Вариант II.

1. Упростите выражение:

а) – 8а · (– 5в); б) 0,5х · (– 2,4у); в) .

2. Приведите подобные слагаемые: .

3. Упростите выражение: .

4. Найдите значение выражения: 3 (5m – 4п) – 4 (3m – 2п), если

m = – 0,2; п = 0,7.
Вариант I.

1. Упростите выражение:

а) – 4с · 3d; б) – 0,2а · (– 3,1в); в) .

2. Приведите подобные слагаемые: .

3. Упростите выражение: .

4. Найдите значение выражения: 5(4а – 3в) – 2(5а – 3в), если

а = – 0,3; в = 0,7.

5. Решите уравнение: .


Вариант II.

1. Упростите выражение:

а) – 8а · (– 5в); б) 0,5х · (– 2,4у); в) .

2. Приведите подобные слагаемые: .

3. Упростите выражение: .

4. Найдите значение выражения: 3 (5m – 4п) – 4 (3m – 2п), если

m = – 0,2; п = 0,7.