сам. алг. 8 класс. Устный счёт 1 Заполнить солнышко. С. Р.1
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
У.Р.№70 Найдите скорость (расстояние, время) тела по следующим данным: а) S = 18 км, t = 2 ч; б) t = 3 с, S = 21 м; в) t =2 мин, υ = 12 м/мин; г) S = 45 км, υ = 5 км/ч; д) t = 7 ч, S = 84 км; е) υ = 11 м/с, t = 9 с; ж) S = 63 м, υ = 9 м/с; з) S = 72 км, t = 3 ч. С.Р.№45 Вариант I На рисунке 1 изображен график, показывающий процесс наполнения бака водой. Ответьте на вопросы: а) Сколько литров воды стало в баке через 2 мин? б) Уменьшался ли в рассматриваемый период объем воды в баке? Если да, то сколько времени? в) Прерывался ли процесс наполнения бака? Если да, то на какое время? г) Менялась ли скорость наполнения бака в течение первых трех минут? Если да, то когда она была наибольшей? Вариант II На рисунке 2 изображен график, показывающий процесс вывоза зерна из хранилища. Ответьте на вопросы: а) Сколько тонн зерна стало в хранилище через 3 ч? б) Увеличивалось ли в рассматриваемый период количество зерна в хранилище? Если да, то сколько времени? в) Прерывался ли процесс освобождения хранилища от зерна? Если да, то на какое время? г) С постоянной ли скоростью шел процесс уменьшения количества зерна в хранилище в течение последних трех часов? Если да, то когда эта скорость была наибольшей? 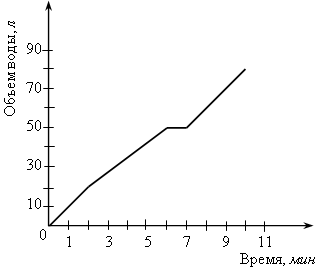 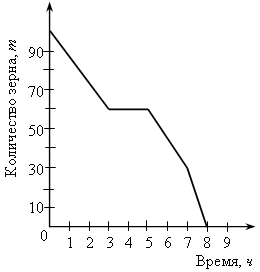 Рис. 1 Рис. 2 У.Р.№71 На рисунке изображен график изменения температуры воздуха в течение 10 часов. 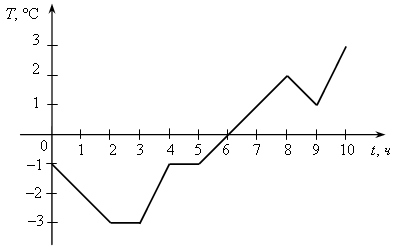 По графику ответьте на вопросы: а) Какая температура была в 3 ч, 7 ч, 9 ч? б) Можно ли определить температуру воздуха в 11 ч? Почему? в) В какое время температура была равна –1 °С; 0 °С; 2 °С? г) Была ли в какое-то время температура равна –4 °С; 5 °С? д) В какое время температура была выше 0 °С; ниже 0 °С? е) В какое время температура повышалась; понижалась; оставалась постоянной? ж) В какое время температура была максимальной, а в какое – минимальной? з) Чему равны максимальная и минимальная температуры за рассматриваемый промежуток времени? У.Р.№72 1. Найдите значение функции y = 2x – 1 для значений аргумента, равного 0; 1; 2; –1. 2. Найдите область определения функции: а) y = 3x – 7; д)  ; ;б) в) y = x3 – 2x2 – 1; ж) г)  . .С.Р.№46 Вариант I 1. Дана функция f (x) = 2x2 – 4x. Найдите f (0) и f (–1). 2. Найдите значение аргумента, при котором функция y = 3x – 2 принимает значение, равное 1. 3. Найдите область определения функции: а) f (x) = 2x – 7; б) f (x) = в*)  Вариант II 1. Дана функция f (x) = 5x2 + x. Найдите f (0) и f (1). 2. Найдите значение аргумента, при котором функция y = 5x + 4 принимает значение, равное –1. 3. Найдите область определения функции: а) f (x) = 3x + 6; б) f (x) = в*)  У.Р.№73 На рисунке изображен график зависимости некоторой величины у от некоторой величины х. 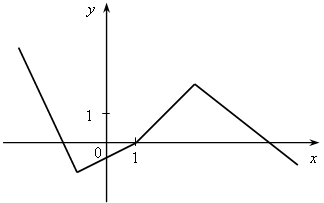 Ответьте на вопросы: а) Чему равно значение у, если х = –3; –1; 2; 5? б) Чему равны значения х, если у = 3; 1; 0; –1? в) Какое минимальное и какое максимальное значения принимает величина у? У.Р.№74 1. Какие из графиков, изображенных на рисунках, являются графиками функций? а) 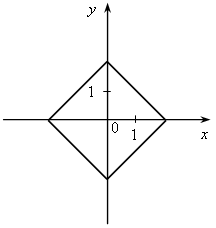 б) б) 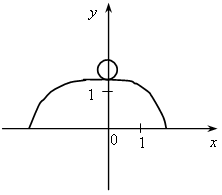 в) 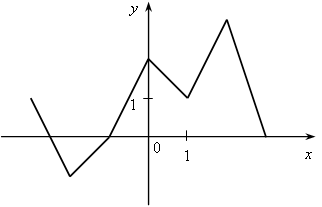 2. По графику, изображенному на рисунке в), найдите: а) значение функции, соответствующее значению аргумента, равному –3; –2; 1; 2; б) значения аргумента, при которых значение функции равно –1; 2; 3; в) координаты точек пересечения с осью х; г) координаты точек пересечения с осью у. С.Р.№47 Вариант I 1. На рисунке 1 изображен график функции y = f (x) на отрезке [–3; 3]. Найдите: а) f (–1), f (0), f (2); б) значения х, при которых f (x) = 3. 2. Дана функция  . Ответьте на вопросы: . Ответьте на вопросы:а) Проходит ли ее график через начало координат? б) Пересекает ли ее график ось ординат; ось абсцисс (если да, то укажите координаты точек пересечения)? в*) Верно ли, что график этой функции целиком расположен в верхней полуплоскости (ответ обоснуйте)? Вариант II 1. На рисунке 2 изображен график функции y = f (x) на отрезке [–3; 3]. Найдите: а) f (–2), f (0), f (1); б) значения х, при которых f (x) = –2. 2. Дана функция  . Ответьте на вопросы: . Ответьте на вопросы:а) Проходит ли ее график через начало координат? б) Пересекает ли ее график ось ординат; ось абсцисс (если да, то укажите координаты точек пересечения)? в*) Верно ли, что график этой функции целиком расположен в верхней полуплоскости (ответ обоснуйте)? 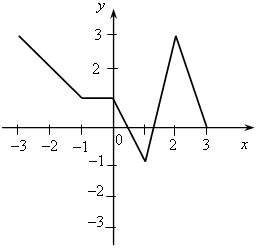 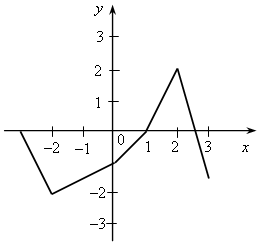 Рис. 1 Рис. 2 С.Р.№48 Вариант I 1. На рисунке 1 изображен график функции y = f (x) на отрезке [–4; 4]. Ответьте на следующие вопросы: а) Есть ли у функции наибольшее и наименьшее значения; если есть, то чему они равны? б) Укажите нули функции. в) Укажите промежутки, на которых функция возрастает. г) Укажите промежутки, на которых функция убывает. 2*. Постройте график какой-нибудь функции, определенной на всей числовой оси, возрастающей при х ≤ 2, убывающей при х ≥ 2, имеющей наибольшее значение, равное 3, и один нуль. Вариант II 1. На рисунке 2 изображен график функции y = f (x) на отрезке [–5; 3]. Ответьте на следующие вопросы: 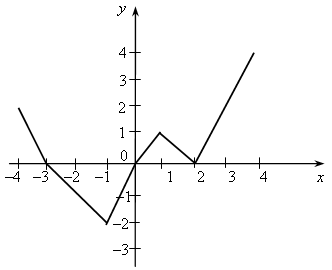 Рис. 1 а) Есть ли у функции наибольшее и наименьшее значения; если есть, то чему они равны? б) Укажите нули функции. в) Укажите промежутки, на которых функция возрастает. г) Укажите промежутки, на которых функция убывает. 2*. Постройте график какой-нибудь функции, определенной на всей числовой оси, убывающей при х ≤ 3, возрастающей при х ≥ 3, имеющей наименьшее значение, равное –2, и один нуль. 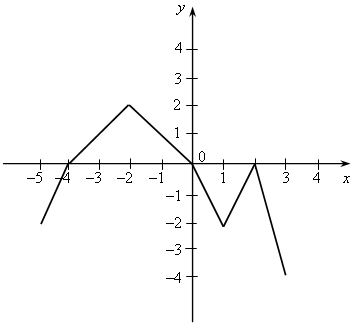 Рис. 2 У.Р.№75 1. Даны уравнения. Какие из них задают прямую? а) y = 2x – 3; в) y = 4 – x; б) y = 3x2 + 1; г) y = 3. 2. Назовите коэффициенты в уравнении прямых: а) y = 4x – 1; в) б) 3. Укажите, у какой из следующих прямых наибольший угловой коэффициент: а) y = 2x + 5, y = 3x – 4, y = 0,7x + 1; б) y = –3x + 1, y = –2x – 3, У.Р.№76 Даны линейные функции: y = 2x + 7; y = –3x; y = 0,4x; 1. Определите, какие из них являются: а) возрастающими; б) убывающими; в) константой; г) прямой пропорциональностью. 2. Графики каких функций а) проходят через начало координат; б) пересекают ось у в точке (0; 2); в) проходят через точку (0; –1). У.р.№77 Даны линейные функции: y = 2x + 3; y = –4x – 1; y = –10; 1. Определите, какие из них: а) являются возрастающими; убывающими; б) являются постоянными; в) возрастают с наибольшей (наименьшей) скоростью; г) убывают с наибольшей (наименьшей) скоростью. С.Р.№49 Вариант I 1. Запишите какую-нибудь формулу, задающую возрастающую линейную функцию. 2. На рисунках а – в изображены графики нескольких функций. На каком из рисунков изображен график линейной функции? 3. Постройте графики функций y = f (x) и y = g (x) и определите значения х, при которых f (x) = g (x); f (x) > g (x). а) f (x) = 3x – 2, g (x) = 1 б*) f (x) = 1, g (x) =  а) 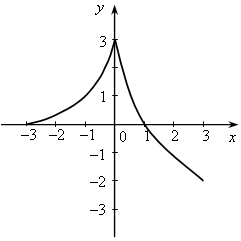 б) б) 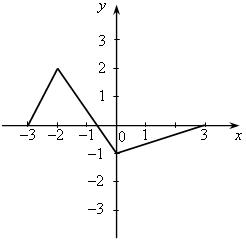 в) 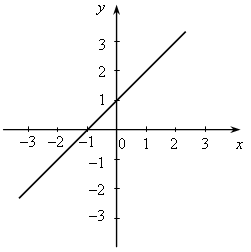 Вариант II 1. Запишите какую-нибудь формулу, задающую убывающую линейную функцию. 2. На рисунках а – в изображены графики нескольких функций. На каком из рисунков изображен график линейной функции? 3. Постройте графики функций y = f (x) и y = g (x) и определите значения х, при которых f (x) = g (x); f (x) > g (x). а) f (x) = 2x + 5, g (x) = –1 б*) f (x) = –1, g (x) =  а) 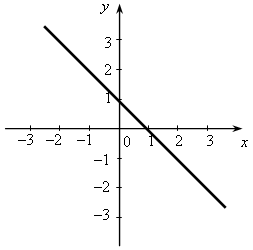 б) б) 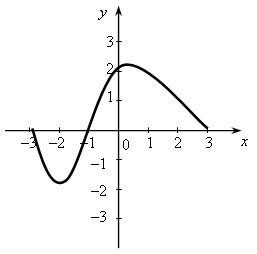 в) 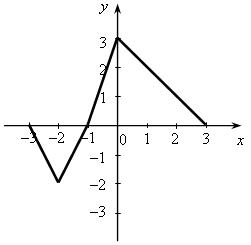 У.Р.№78 Выразите из формулы переменную х: а) y = x ∙ z; г)3a = c ∙ x; б) a = b ∙ x;д) y = 2xz; в) t = 7x;е) p2 = –4tx. С.Р.№50 Вариант I Дана функция f (х) = а) Найдите значения f (–3); f (–1); f (2); f (4). б) Постройте график функции y = f (х). в) Укажите, при каких значениях х значения функции положительны, при каких отрицательны. г) Ответьте, убывает ли эта функция на луче х < 0. д) Укажите, при каких значениях х значение функции равно –2; 32. е*) Укажите, при каких значениях х значение функции меньше Вариант II Дана функция f (х) = а) Найдите значения f (–2); f (–1); f (3); f (6). б) Постройте график функции y = f (х). в) Укажите, при каких значениях х значения функции положительны, при каких отрицательны. г) Ответьте, возрастает ли эта функция на луче х > 0. д) Укажите, при каких значениях х значение функции равно 2; –36. е)* Укажите, при каких значениях х значение функции больше – Зачет № 5. Функции
Вариант I Обязательная часть. 1. Функция задана формулой f (х) = х2 – 9. а) Найдите f (6), f (–0,5). б) Найдите значение аргумента, при котором значение функции равно –9; 7. 2. Функция задана формулой y = –2х + 3. а) Постройте график функции. б) Возрастающей или убывающей является функция? 3. В первой строке таблицы указано время движения автобуса из города А в город В, а во второй – расстояние автобуса от города А:
а) Постройте график движения автобуса. б) Определите, на каком примерно расстоянии от А находился автобус через 2,5 ч после начала движения. в) В какой промежуток времени скорость была наибольшей? Дополнительная часть. 4. Найдите область определения функции:  . .5. Постройте график функции:  6. Задайте формулой какую-нибудь функцию, график которой пересекает ось х в точках (–1; 0), (2; 0), (5; 0). Вариант II Обязательная часть. 1. Функция задана формулой f (х) = 16 – х2. а) Найдите f (0,5), f (–3). б) Найдите нули функции. 2. Функция задана формулой f (х) = а) Постройте график функции. б) Укажите значения х, при которых значения функции больше нуля, меньше нуля. 3. В таблице приведены данные о росте ребенка в первые пять месяцев его жизни:
а) Постройте график роста ребенка. б) Определите, каким примерно был рост ребенка в 2,5 месяца. в) В какие месяцы ребенок рос с одинаковой средней скоростью? Дополнительная часть. 4. Найдите область определения функции:  . .5. Постройте график функции:  6. Задайте формулой какую-нибудь функцию, график которой проходит через начало координат и пересекает ось х в точках (–3; 0), (1; 0). |
