В. Г. Шуваев Замкнутые системы управления электроприводом
 Скачать 1.57 Mb. Скачать 1.57 Mb.
|
|
Раздел 3. Расчет динамики электропривода В данном разделе рассматривается возможность получения динамических показателей работы спроектированного электропривода, в соответствии с заданными, т.е. строится и анализируется переходный процесс в системе электропривода. Под переходными процессами понимают процессы, происходящие в электроприводе при переходе его из одного установившегося состояния в другое, когда изменяется скорость, момент и ток. Переходные процессы играют огромную роль в работе электропривода и рабочей машины. Характер их протекания предопределяет производительность машины, качество выпускаемой продукции, а также заметно сказывается на режимах работы электропривода. Вид переходного процесса зависит от свойств всех элементов привода и рабочей машины. В этом разделе требуется: уяснив работу электропривода по структурной схеме, составить передаточные функции элементов системы, составить передаточную функцию замкнутой системы; проверить систему на устойчивость, синтезировать (если необходимо) корректирующее устройство; построить переходный процесс по управляющему и возмущающему воздействиям и определить показатели качества работы системы; оценить работу системы электропривода по переходному процессу; вычертить структурные схемы нескорректированной и скорректированной систем. 3.1. Составление структурной схемы электропривода для расчета динамики На основе функциональной схемы (см.рис.2.1) можно составить обобщенную структурную схему замкнутой системы ЭП со всеми ОС (рис.3.1). 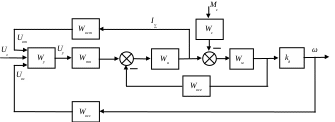 Рис.3.1. Обобщенная структурная схема замкнутой системы электропривода В курсовом проекте можно ограничиться расчетом динамики системы, не учитывая задержанную ОС по току, вследствие её нелинейности и сложности расчетов. Поэтому обобщенную схему (см.рис.3.1) можно представить, как показано на (рис.3.2). 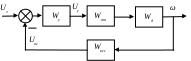 Рис.3.2. Упрощенная структурная схема замкнутой системы электропривода Упрощенная структурная схема (см.рис.3.2) представляет собой упрощенную математическую модель системы. Первоначально структурная схема вычерчивается без корректирующих звеньев, а после их выбора и расчета приобретает окончательный вид. 3.2. Составление передаточных функций элементов 3.2.1. Составление передаточной функции двигателя постоянного тока [3,4] Частотные методы исследования и аппарат передаточных функций весьма эффективны при исследовании линейных систем. К таким системам можно отнести ЭП постоянного тока с двигателями независимого возбуждения при постоянном магнитном потоке Φ = const. Для ЭП с двигателями последовательного и смешанного возбуждения приходится использовать приближенные методы исследования, разработанные для нелинейных систем. Посмотрим, как можно составить передаточную функцию и структурную схему двигателя постоянного тока независимого возбуждения при постоянном магнитном потоке. В соответствии с рис.2.2, с учетом того что обратная связь по току не действует, а момент статической нагрузки равен нулю, можно составить передаточную функцию двигателя постоянного тока независимого возбуждения 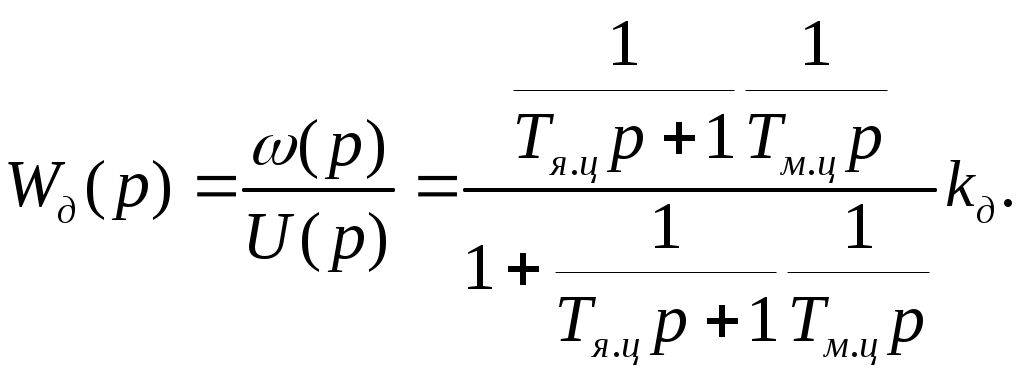 Преобразуя данное выражение, получаем Приведем передаточную функцию к виду, удобному для логарифмирования [15]: где коэффициенты Т1 и Т2 необходимо рассчитать. Если Тм>4Тя, то, решая систему (3.3), 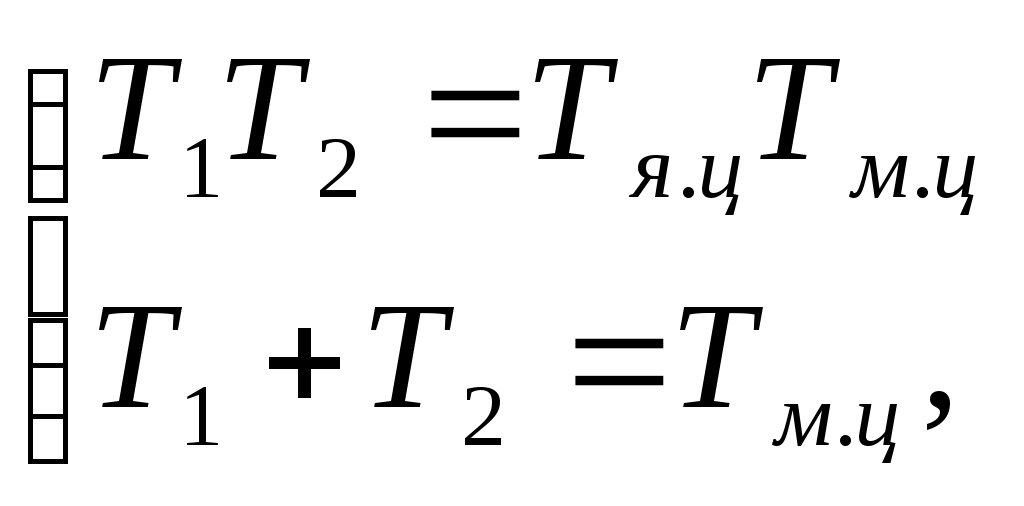 (3.3) (3.3)получим необходимые значения Т1 и Т2. Если Тм< 4Тя, то передаточная функция двигателя будет представлена колебательным звеном: где коэффициенты Т и рассчитываются по формулам фиктивная постоянная времени коэффициент затухания: Т.к. рассматриваем систему ЭП, то во всех этих выражениях постоянные времени Тя.ц и Тм.ц и конструктивный коэффициент двигателя kд необходимо взять из табл.1.6. На основании рис. 3.3, для исследования влияния возмущающего воздействия (полагая Uз=const) и в соответствии с приведенным выводом, запишем передаточную функцию двигателя по моменту 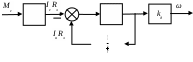 Рис 3.3. Структурная схема двигателя по моменту 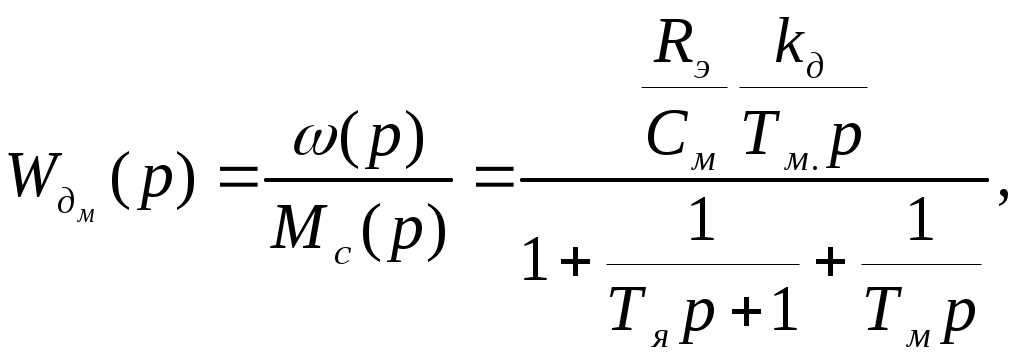 преобразуя, получим где В расчете принимаем Се = См = С, где С коэффициент двигателя (см. табл. 1.6). 3.2.2. Составление передаточной функции тиристорного преобразователя Передаточную функцию тиристорного преобразователя (управляемого выпрямителя) представим в виде где значение коэффициента передачи тиристорного преобразователя kтп можно взять из табл.1.6, а постоянная времени Тт.п складывается из постоянной времени фильтра на входе системы импульсно-фазового управления Тф (Тф≈0,005с) и среднестатистического запаздывания преобразователя т.п [1;6]. Передаточная функция системы импульсно-фазового управления преобразователем представлена звеном «чистого» запаздывания: Звено «чистого» запаздывания при условии малого т.п можно представить апериодическим звеном первого порядка: где т.п=1/(2mfc) - запаздывание преобразователя, где m=6 фазность преобразователя (для трехфазной мостовой схемы). Таким образом, полная постоянная времени тиристорного преобразователя 3.2.3. Составление передаточной функции цепи ОС по скорости В соответствии со структурой рис.2.2 в цепи ОС по скорости мы имеем устройство (рис.3.4), 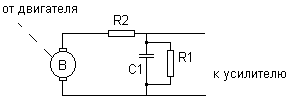 Рис.3.4. Устройство ОС по скорости где датчиком скорости является тахогенератор, на выходе которого стоит фильтр, гасящий нежелательные пульсации. В общем случае передаточную функцию цепи обратной связи по скорости можно записать W(p)=kтгWф.тг(p), (3.11) где коэффициент передачи тахогенератора kтг известен (см.табл.1.6). Передаточную функцию фильтра представим как 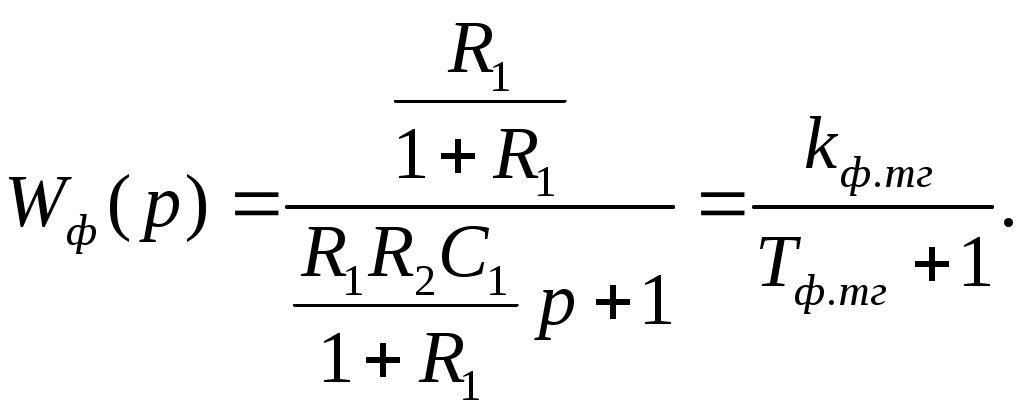 (3.12) (3.12)Рекомендуется постоянную времени фильтра Тф.тг брать в пределах 0,003 .. 0,005 с [6;10]. Постоянную времени фильтра датчика тока (для раздела 2) рекомендуется взять примерно равной постоянной времени фильтра датчика скорости [10]. Исходя из этого условия и задаваясь значениями R1, R2, C1, можно определить коэффициент передачи фильтра. Т.к. на этапе нахождения регулируемого коэффициента ОС по скорости мы принимали, что коэффициент передачи фильтра равен единице, то в регулируемый коэффициент ОС по скорости надо внести поправку b`с=bc/ kф.тг . (3.13) Тогда передаточную функцию цепи ОС по скорости можно записать в виде 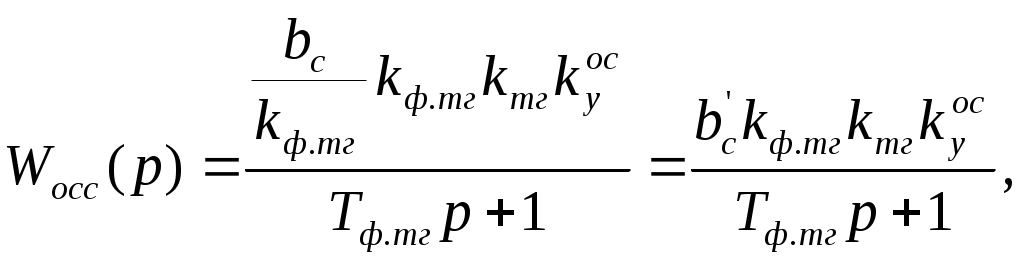 (3.14) (3.14)где Тф.тг=0,0030,005 с. 3.3. Составление передаточной функции системы Первоначально структурная схема вычерчивается без корректирующих звеньев, а после их выбора и расчета структурная схема приобретает окончательный вид. Таким образом, в соответствии с рис.3.2 имеем следующую структурную схему системы ЭП постоянного тока с тиристорным управляемым выпрямителем (рис. 3.5): 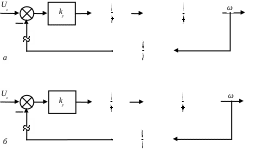 Рис.3.5. Расчетная схема ЭП Расчет устойчивости системы ЭП будем проводить по разомкнутой системе, структурная схема которой показана на рис.3.5. Рис.3.5а, соответствует системе, двигатель в которой представлен колебательным звеном, а рис.3.5б апериодическим звеном второго порядка. Составим передаточную функцию разомкнутой системы Wраз(p)= Wу(p)Wт.п(p)Wд(p)Wocс(p) . (3.15) Получим функцию вида или Передаточную функцию системы можно упростить, если малые постоянные времени фильтра ОС по скорости и тиристорного преобразователя объединить [10], т.е. (Тт.пр+1)(Тф.тгр+1)=Тэсp+1 , где Тэс=Тт.п+Тф.тг . (3.18) 3.4. Проверка устойчивости системы электропривода Для расчета устойчивости систем регулирования применяются различные методы. Наиболее распространенным является метод, основанный на построении логарифмических частотных характеристик. Критерий устойчивости Найквиста применим и в случае изображения амплитудно-фазовых характеристик в виде логарифмических амплитудной и фазовой частотных характеристик разомкнутой системы. Необходимым и достаточным условием устойчивости системы является пересечение логарифмической амплитудно-частотной характеристикой (ЛАЧХ) разомкнутой системы оси абсцисс раньше, чем логарифмическая фазно-частотная характеристика (ЛФЧХ) пересечет линию, соответствующую ее фазовому сдвигу . Для проверки устойчивости системы электропривода необходимо построить на одном графике логарифмические амплитудную и фазную частотные характеристики и применить критерий Найквиста. 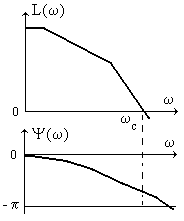 Рис.3.6. Характеристики устойчивой системы Просто и удобно строить характеристики с использованием пакета MathCad на персональной ЭВМ. Для этого воспользуемся формулами: вещественная частотная характеристика мнимая частотная характеристика амплитудно-частотная характеристика логарифмическая амплитудно-частотная характеристика логарифмическая фазно-частотная характеристика или где, например, Построив графики в логарифмическом масштабе, можем получить следующие характеристики (рис. 3.7): 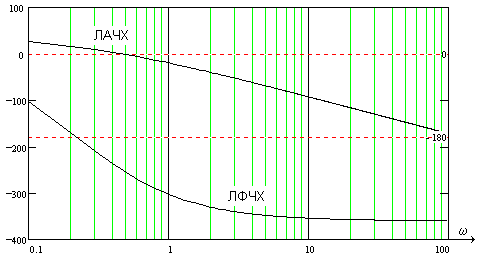 Рис.3.7. Характеристики неустойчивой системы электропривода Видим, что система неустойчива, т.е. необходимо вводить корректирующие устройства. В том случае если бы система была устойчива и имела бы необходимые запасы устойчивости по амплитуде и по фазе, можно было бы сразу переходить к построению переходного процесса в системе электропривода. Однако если показатели качества не удовлетворяют заданным, то систему придется корректировать. 3.5. синтез корректирующего устройства Корректирующее устройство должно обеспечивать отсутствие статической ошибки регулирования, ограничить (не более заданного) перерегулирование и время регулирования [15]. Для корректировки рассчитываемой системы электропривода предлагается использовать последовательное корректирующее устройство, как более простое для расчета и более универсальное. Не возбраняется использовать для этих целей параллельное корректирующее устройство, синтез которого подробно рассмотрен в [15;16]. Синтез корректирующего устройства осуществляется в несколько этапов. Во-первых, необходимо построить асимптотические логарифмические характеристики системы электропривода. Для этого необходимо ранжировать постоянные времени в передаточной функции системы по убыванию, начиная с наибольших. Например, Т2>T3>T1. Необходимо отметить значения 1/Тi на оси абсцисс. Далее надо найти значение выражения 20g(k), где k коэффициент усиления системы. С точки (0; 20lg(k)) начнем построение асимптотической логарифмической характеристики. Коэффициент k определяет в (3.16) и (3.17) горизонтальную линию с наклоном 0 дб/дек, до первой точки 1/Тi. Далее множитель (Тip+1)-1 с соответствующим значением Тi определяет наклон характеристики на –20 дб/дек, а множитель (Т2р2+2Тр+1) наклон характеристики на –40 дб/дек после отметки 1/Тi. Наклон последующих отрезков характеристики получается простым алгебраическим сложением (например, -20+(20)= 40 дб/дек). Типичные асимптотические логарифмические амплитудно-частотные характеристики представлены на рис.3.8. 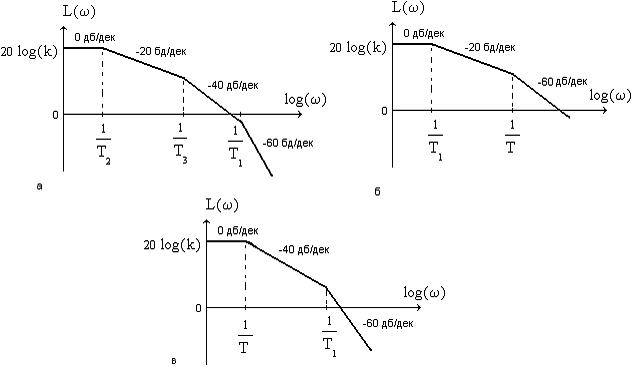 Рис.3.8. Типичные асимптотические ЛАЧХ системы Для передаточной функции системы вида (3.16) асимптотическая ЛАЧХ будет иметь вид рис.3.8а; для передаточной функции вида (3.17) рис.3.8б при 1/Т1<1/T и рис.3.8в, при 1/Т<1/Т1. Во-вторых, по заданным показателям качества необходимо найти частоту среза желаемой системы. Воспользовавшись номограммами В.В Солодовникова. [1], рис.3.9, определим желаемую частоту среза, т.е. частоту, при которой желаемая асимптотическая амплитудно-частотная характеристика пересечет нулевую ординату. ωс.ж определяется по заданному времени переходного процесса tп и перерегулированию σ, с помощью уравнения (3.19): 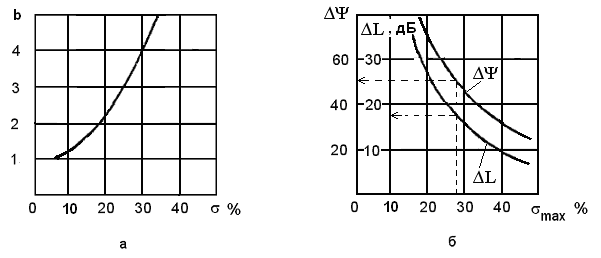 Рис.3.9. Номограммы для определения частоты среза (а) и частоты сопряжения (б) В формуле (3.19) – b–коэффициент, зависящий от перерегулирования и определяемый по графику (рис. 3.9а). Учитывая, что среднечастотная асимптота (СЧА) определяет качество переходного процесса системы и запас ее устойчивости по амплитуде и фазе, построение ее осуществляют в соответствии с рекомендациями [1], обеспечивающими требуемое качество процесса. СЧА проходит через ωс.ж с наклоном -20дБ/дек, в диапазоне частот обычно не менее одной декады. Это дает достаточный запас устойчивости по модулю. При построении СЧА может быть учтен требуемый запас устойчивости по модулю, определяющий частоту сопряжения СЧА с отрезком, сопряженным с низкочастотной асимптотой (НЧА). Значение требуемого запаса устойчивости по модулю и фазе находится по графику (рис. 3.9б) в зависимости от заданного перерегулирования σ. Затем необходимо построить желаемую асимптотическую логарифмическую амплитудно-частотную характеристику системы [15]. Построение желаемой характеристики (рис.3.10) начинаем со среднечастотного участка (СЧУ). Через точку с координатами (с;0) проводим прямую (1) с наклоном –20 дб/дек. Эта прямая будет ограничиваться в длину тем, что расстояние от нее до оси абсцисс не должно превышать запаса устойчивости по амплитуде (выберите его в пределах 1520 дб). Приступим к построению низкочастотного участка (НЧУ). Это будет прямая (2) с наклоном –20 дб/дек (для исключения статической ошибки регулирования), которая проходит из области низких частот, а именно из точки (lg()=0; 20lg(k)), до первой частоты сопряжения. Таким образом, получаем две прямые с наклоном –20 дб/дек, которые в области низких частот можно соединить прямой (3) с наклоном –40 дб/дек. Высокочастотную часть (4) строим параллельно высокочастотной части асимптотической амплитудно-частотной характеристики некорректированной системы (см.рис.3.10). 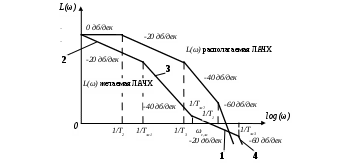 Рис.3.10. Пример построения желаемой асимптотической ЛАЧХ системы В-четвертых, необходимо построить логарифмическую характеристику корректирующего устройства. Построение асимптотической характеристики корректирующего устройства проводим исходя из соображения, что L()к=L()жL()р. (3.20) Таким образом, строя характеристику корректирующей цепи, необходимо графически вычесть характеристику нескорректированной системы из характеристики желаемой системы. Сделаем это ( рис.3.11). 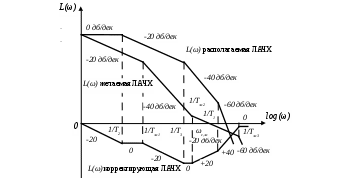 Рис.3.11. Построение асимптотической ЛАЧХ корректирующей цепочки После этого необходимо получить передаточную функцию корректирующего устройства. Перед выбором корректирующей цепочки сделаем несколько замечаний. Пассивные RC-цепи формируют амплитудно-частотную логарифмическую характеристику только под осью абсцисс, т.е. с коэффициентом усиления k<1. Характеристику над осью абсцисс, т.е. с k>1, формируют активные корректирующие цепочки на операционных усилителях. Если в передаточной функции корректирующей цепочки стоит интегрирующее звено, то первый отрезок логарифмической амплитудно-частотной характеристики наклонен на –40 дб/дек. Передаточную функцию корректирующей цепочки формируют посредством составления ее числителя и знаменателя из сомножителей (Тiр+1). Несмотря на то что получилась такая сложная характеристика, достаточно просто найти ее передаточную функцию. На первом участке звено (Т1p+1), на втором звено (Т2p+1), которое определяет прямую с наклоном +20 дб/дек, а в итоге два звена дают 0 дб/дек. Таким образом получаем передаточную функцию корректирующего устройства: где Тк1>>1, тогда 1/Тк10; Тк2=Т2; Тк3=Тж1; Тк4=Т3; Тк5=Тж2; Тк6=Т1;Тк7Тк8=Тж3. Корректирующие звенья выбираются из таблицы. П6 [15]. Для данной корректирующей цепочки приемлемой будет структура, набранная из звеньев, представленных на рис 3.12, 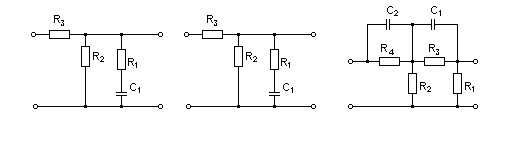 Рис.3.12. Корректирующие звенья где постоянные времени, а следовательно, и номиналы RC-элементов, можно найти из (3.21). 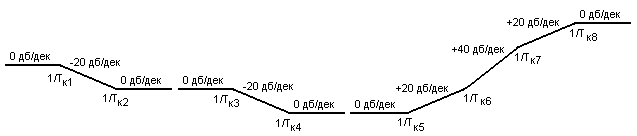 Для цепочки рис.3.12 можно начертить следующие асимптотические логарифмические амплитудные характеристики: Для цепочки рис.3.12 можно начертить следующие асимптотические логарифмические амплитудные характеристики:а б в Рис.3.13. Характеристики корректирующей цепочки Таким образом, видим, что характеристика корректирующей цепочки (рис.3.13) практически совпала с построенной на рис.3.11. Мы получили довольно сложное корректирующее устройство, его можно упростить, если следовать рекомендациям при построении желаемой ЛАЧХ: НЧУ и ВЧУ строятся так, чтобы оба или один из них (чаще НЧУ) в возможно большем диапазоне частот совпадали с ЛАЧХ нескорректированной системы; СЧУ сопрягается с НЧУ и ВЧУ прямыми с наклоном -20; -40; -60 дб/дек. Желательно, чтобы эти сопряжения отличались от наклона ЛАЧХ нескорректированной системы в том же диапазоне частот, не более чем на 20 дб/дек; сопряжение участков проводится в тех же точках, что и сопряжения ЛАЧХ нескорректированной системы. Определив передаточную функцию скорректированной системы, проверим ее на устойчивость и определим запасы по амплитуде и по фазе. Запасы по амплитуде Lа и по фазе Lf можно определить, построив логарифмические характеристики как показано в п.3.4 [15]. Эти значения могут использоваться для сравнения с нормами запасов по амплитуде и по фазе, обеспечивающими удовлетворительные показатели качества в системах управления и регулирования. 3.6. Построение переходного процесса в системе ЭП. Качество работы ЭП, как и любой системы управления, оценивается по переходным процессам. Особенностью оценки ЭП является то, что нас интересует переходный процесс не только по управлению (изменение задания скорости привода, работающего с нагрузкой), но и по возмущению (изменение момента нагрузки – «сброс» или «наброс» нагрузки). В последнем случае, учитывая, что момент прямо пропорционален току, часто строят переходный процесс по току якоря. В целом методика построения переходного процесса ничем не отличается от традиционной. Например, для построения переходного процесса системы управления ЭП постоянного тока по управлению необходимо составить передаточную функцию скорректированной замкнутой системы пользуясь правилом Представим полученную передаточную функцию в виде полинома 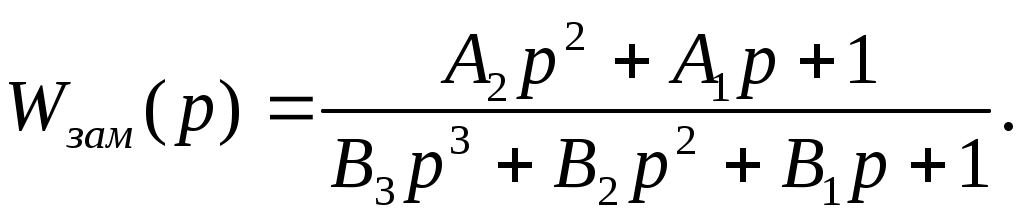 (3.23) (3.23)Для получения переходного процесса нужно передаточную функцию умножить на изображение ступенчатого воздействия 1/р и воспользоваться обратным преобразованием Лапласа, в результате получим выражение вида Для построения переходного процесса удобно использовать один из известных пакетов: MathCAD, MathLAB, МикАл. Для построения переходного процесса по возмущению необходимо предварительно составить структурную схему и определить передаточную функцию замкнутой скорректированной системы по моменту. 3.7. Оценка качества переходного процесса Устойчивость является необходимым, но недостаточным условием работоспособности систем автоматического регулирования. Устойчивость системы регулирования означает лишь то, что в системе происходит затухание переходного процесса при воздействии управляющего или возмущающего внешних сигналов. Время затухания процесса, максимальное отклонение регулирующей величины и число колебаний в системе при этом не определяются, однако эти величины являются очень важными показателями качества процессов регулирования. Рассмотрим основные показатели качества систем автоматического регулирования, пользуясь характеристикой переходного процесса (см.рис.3.14). Первый показатель качества перерегулирование Второй показатель качества позволяет оценить быстродействие системы и называется временем регулирования (временем переходного процесса) tп. 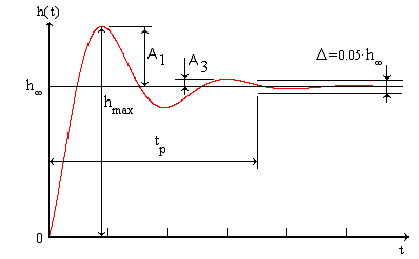 Рис.3.14. График переходного процесса Учитывая, что полное затухание в системе происходит лишь при t, условно стали считать окончанием переходного процесса точку пересечения графика процесса с линиями, отстоящими на 5% от установившегося значения регулируемой величины. Третий показатель качества характеризует число колебаний Nр регулируемой величины в течение времени переходного процесса (это число переходов через установившееся положение за время регулирования). Далее выделяются такие показатели, как степень затухания и показатель колебательности. Степень затухания характеризует быстроту затухания колебаний регулируемой величины относительно установившегося значения и рассчитывается по формуле где Аi отклонение регулируемой величины от установившегося значения (+/). Чем больше степень затухания, тем быстрее регулируемая величина придет к установившемуся значению. Показатель колебательности характеризует склонность ЭП к колебаниям и определяется Чем больше показатель колебательности, тем меньше колебаний относительно установившегося значения совершит регулируемая величина до того, как придет к установившемуся значению. Кроме того, оценивается максимальное динамическое отклонение регулируемой величины в переходном процессе А1и статическая ошибка δ, если она имеет место. Определив все эти показатели, составим сводную табл. 3.1. Таблица 3.1 Сравнение показателей качества
|
