дидактические материалы. Дидактические материалы по МПМ в нач. кл.. В. Н. Медведская Дидактические материалы по методике преподавания математики в начальных классах
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
ДЕЯТЕЛЬНОСТЬ УЧИТЕЛЯ И УЧАЩИХСЯУчитель проводит игру «Плюс-минус»: прикрепляет на доске карточку № 8 и предлагает классу пальцевыми знаками (+, -) показать, какими действиями можно ответить на вопрос каждой из следующих задач, а затем объяснить свой выбор. Из гаража выехало сначала 4 машины, а потом еще 5 оставшихся машин. Сколько машин было в гараже? На полке стояло 8 книг. 2 из них положили в ранец. Сколько книг осталось на полке? – Составьте обратные задачи: о машинах в гараже, чтобы она решалась вычитанием, а про книги на полке – сложением. При обосновании выбора арифметического действия от учащихся требуется употребление терминов: «больше», «да еще», «целое», «меньше», «без», «часть». Учитель подводит итоги проведенного блиц-опроса и сообщает: «Сегодня мы будем учиться решать новые задачи». Составленную задачу про книги совместно моделируют на схеме краткой записи; учащиеся повторяют ее текст, решение записывают. Было – ? кн. Взяли – 2 кн. 6+2=8 (кн.) Осталось – 6 кн. Ответ: 8 книг было. – Почему эта задача решается сложением? (Сначала на полке книг было больше: 6 да еще 2). – Чтобы проверить себя, сделаем с помощью отрезков рисунок к данной задаче. Учитель на доске прикрепляет карточку №4  и под его руководством учащиеся, комментируя каждый шаг, изображают у себя в тетрадях Было  (1) ВзялиОсталось Последущая беседа проводится с опорой на эту графическую модель. – Что обозначает число 2? (Это – часть всех книг, которые стояли на полке.) – Что обозначает число 6? (Это – другая часть всех книг, которые стояли на полке.) – Что в задаче надо найти? (Надо найти целое, состоящее из двух частей: «взяли» и «осталось».) У |
| Этапы работы над задачей и используемые приемы | Деятельность учителя | Деятельность учащихся |
| I. Восприятие и осмысление содержания задачи | Предлагает прочитать задачу «про себя» и приготовиться к выразительному громкому чтению. | При чтении «про себя» выделяют главные опорные слова. |
| а) чтение задачи | Задача: «На озере ловили рыбу 14 рыбаков. Пятеро рыбаков ушли, а двое пришли. Сколько стало рыбаков?» Выставляет карточку.  Вызывает одного ученика для чтения вслух. Спрашивает, услышали ли ученики важные слова. При необходимости предлагает прочитать задачу еще раз. | Читает ученик, остальные слушают. Высказывают свою точку зрения о правильности выделения опорных слов или читают задачу по-другому. |
| б) прикидка ответа | Ставит вопрос: «Можно ли сразу сказать, рыбаков стало больше, чем было, или меньше?» | Высказывают мнения. Например, а) «Рыбаков стало больше, потому что двое пришли»; б) Рыбаков стало меньше, т.к. ушло пятеро, а пришло только двое». |
| в) графическое моделирование | Что подсказывает карточка? П  редлагает редлагает проверить предположения с помощью чертежа (самостоятельная работа). Наблюдает за работой, уточняет детали, оказывает индивидуальную помощь. На доске: 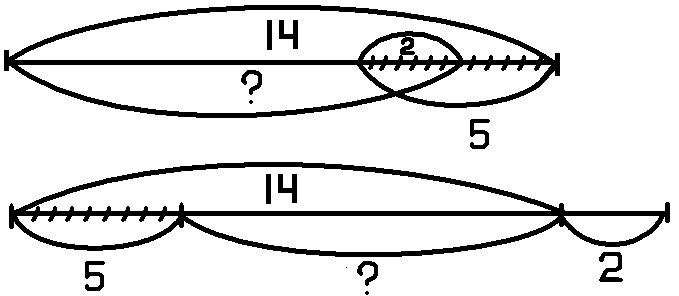 Организует обсуждение чертежей: Как показаны данные задачи, вопрос? Какой чертеж лучше? понятнее? (При необходимости использует заготовленный заранее чертеж). | - Сделать рисунок (схему, чертеж) к задаче. Два ученика на доске, остальные в тетради самостоятельно выполняют чертеж к задаче. Сравнивают, обсуждают, вносят исправления. |
| II. Поиск решения (обсуждение готовых вариантов) | Беседа: - Показывают ли чертежи сколько рыбаков стало на озере? - Показывают ли чертежи, как узнать, сколько рыбаков стало на озере? Сообщает детям, что учителю чертежи «подсказали» (Незнайка по чертежам нашел) несколько способов решения и предъявляет их (запись заранее готовится на доске): I. 1) 14+5=... II. 1) 14-5=... 2) 19-2=... 2) 9+2=... III. 1) 5-2=... IV. 1)5-2=... 2) 14+3=... 2)14-3=... V. I) 14+2=... 2)16-5=... Предлагает объяснить смысл действий в записанных способах и выбрать решение задачи. | Отвечают. Анализируют выбранный чертеж и устанавливают соответствие между моделью (чертежом) и оригиналом (текстом задачи). Выделяют на чертеже взаимосвязи между данными и искомым. Анализируют решения. Обосновывают выбор действий по чертежу, выбирают правильные способы решения: II, IV, V. |
| III. Решение задачи (математическое моделирование) | Предлагает записать в тетради решение задачи одним из способов по действиям с пояснениями (для желающих – два способа). | Самостоятельная работа: объясняют себе смысл числовых данных из условия задачи, смысл каждого числового выражения (каждого выполненного действия), соотносят окончательный результат с вопросом задачи, дают ответ задачи. |
| IV. Проверка решения Способы проверки: а) повторное комментирование плана решения и вычислений; б) сравнение ответов в разных способах решения. | П  редъявляет карточку редъявляет карточку и выясняет, о чем она напоминает. Организует проверку решения задачи. | - Необходимо проверить, правильно ли решена задача. Комментируют записанные в тетради решения. Сравнивают ответы в разных способах решения, вспоминают прикидку ответа и сравнивают полученный ответ с ней. |
| V. Творческая работа. Цель работы: выяснить, как влияют на решение задачи опорные слова. Форма творческой работы: изменение условия задачи. | Предлагает изменить условие задачи так, чтобы а) решение I было верным; б) оба действия в решении были сложением. Выясняет, почему решение III не является правильным. | Предлагают изменения, обосновывают их, обсуждают предложения. |
4. СЛОВАРЬ ТЕРМИНОВ
МЕТОДИКИ ПРЕПОДАВАНИЯ МАТЕМАТИКИ
В НАЧАЛЬНЫХ КЛАССАХ
Любая наука наряду с естественным (обычным родным для человека) языком использует собственный язык для обозначения специальных понятий, терминов. Поскольку методика преподавания математики в начальных классах тесно связана с другими науками (математика, психология, педагогика, дидактика и пр.), то в ней обязательно применяется широкий круг соответствующих терминов, например, «множество», «число», «возрастные особенности», «логическое мышление», «воспитание», «обучение», «развитие», «принцип систематичности», «познавательная деятельность» и т.д. В то же время у методики, как и у других наук, есть свой тезаурус, т.е. словарь, стремящийся максимально охватить лексику ее языка.
Термины, которыми оперирует методическая наука, заменяют, как правило, достаточно многословные описания, характеризующие смысловое содержания объектов изучения или применения. Например, словосочетание «числовая лента» заменяет обобщенное описание существенных структурных признаков данного средства наглядности, которому можно придавать различную материализованную форму – самодельная лента с нанесенным на нее отрезком натурального ряда чисел, масштабная линейка, складной метр и др. Термин «числовая лента» является одним из примеров лексической единицы языка методики преподавания математики в начальных классах или ее дескриптором (от латинского describo – описываю). Таким образом, тезаурус методики – это словарь дескрипторов, т.е. слов или словосочетаний, которым в этой науке придается согласованно однозначный смысл, что позволяет экономно обмениваться точной, одинаково трактуемой в данной области знания научной информацией, осознанно сохранять ее в памяти, а значит, способствует становлению профессиональной грамотности, компетентности, культуры учителя.
Цель работы со словарем терминов – усвоение лексики языка методики преподавания математики в начальных классах. (Не овладев языком науки, можно ли освоить саму науку?!)
Содержание работы – перевод указанных в словаре терминов на естественный язык с опорой на воображение, представление, конкретизацию в предметной форме, в виде схематического рисунка, конструкции, чертежа, математического примера и др.; в некоторых случаях это перевод на язык математических дефиниций, т.е. определений, например, «натуральное число», «счет», но с обязательной последующей конкретизацией.
Организация работы со словарем
Термины в словаре размещены по двум разделам курса методики: общая методика и частная методика. Для частной методики они разбиты на подразделы, каждому из которых присвоены номер и «имя» – название основных разделов начального курса математики. Это поможет вам в поиске соответствующего дескриптору смыслового содержания в методической литературе или в текстах лекций. Его следует искать в контексте изложения учебного материала, а не в виде явно зафиксированного и оформленного определения, как это принято в математической науке.
В каждом подразделе используется внутренняя нумерация. Например, номер 3.12 означает, что соответствующий термин в словаре надо искать в третьем подразделе на 12-м месте. Тире после каждого включенного в словарь слова или словосочетания служит сигналом напоминания необходимости раскрыть его смысловое содержание. В данном словаре вы встретите несколько примеров уже выполненного перевода. Остальные термины вам надо «расшифровать» самостоятельно. Прочитав тот или другой термин, задайте себе вопросы:
Где мне уже встречался этот термин?
Что я под ним понимаю?
Могу ли я объяснить его смысл словами?
Могу ли я как-то проиллюстрировать его смысл (наглядным изображением, образно, описанием некоторой конкретной ситуации и др.)?
В каких ситуациях можно применять данный термин?
Есть ли другие, заменяющие его термины?
С какими терминами он связан?
В случае затруднений или сомнений, а также для установления согласованности между смыслом, вкладываемым вами в термин и его однозначно принятым в науке содержанием, обращайтесь за подсказкой к соответствующему разделу или параграфу в учебных пособиях по методике. Номера терминов, смысл которых вам не удалось расшифровать самостоятельно, запишите, чтобы затем уточнить их содержание в беседе с преподавателем.
Итог работы со словарем – уверенное и осознанное, наполненное общепринятым конкретным содержанием, владение языком методики преподавания математики в начальных классах.
Самоконтроль полезно осуществлять систематически по ходу изучения тем курса методики.
Самооценка – выбираю в словаре любой дескриптор (термин) и отвечаю себе на вопросы: «Понимаю его смысл? Могу его расшифровать? Могу правильно применить? Уверен в том, что правильно понимаю этот термин?»

 читель выставляет опору
читель выставляет опору