Вычислительный эксперимент в методах диагностики микро и наноструктур

• Название: Вычислительный эксперимент в методах диагностики микро и наноструктур
• Дата: 01.07.2022
• Размер: 2.33 Mb.
• Имя файла: razdel_3.doc
• Тип: Документы; #622327
• страница: 1 из 6

Раздел 3. Вычислительный эксперимент в методах диагностики микро - и наноструктур

Разработка методов диагностики и анализа требует проведения большого числа расчётов, целью которых является выяснение возможностей исследуемых методов и их отработка. Варьируемыми при таких расчётах являются модели объектов и измерительных воздействий, их изменяемые и постоянные параметры, различные погрешности измерений и диапазоны измеряемых величин. Эффективность проведения вычислительных экспериментов определяет во многом эффективность разработки и возможностей использования методов.

Вычислительный эксперимент можно определить как эксперимент над математической моделью метода исследования объекта. Модель метода исследования объекта представляется совокупностью модели самого объекта, модели взаимодействия объекта и измерительного воздействия с учетом воздействия окружающей среды на процесс измерения. Реализация вычислительного эксперимента состоит в вычислении на ЭВМ параметров модели на основе полученных данных (экспериментальных или модельных), по значениям которых делаются выводы о свойствах объекта исследования.

Вычислительный эксперимент дополняет эксперимент натурный, позволяя:

• 
  проверить соответствие используемых моделей объектам и методам
  

• 
  найти оптимальные условия измерений;
  
• 
  определить точность и область чувствительности выбранного метода;
  
• 
  определить неизвестные параметры объекта по экспериментальным данным натурного эксперимента;
  
• 
  установить степень влияния погрешностей измерения на значения определяемых параметров;
  

В отличие от натурного эксперимент вычислительный часто требует меньших затрат ресурсов - оборудования, времени, обслуживающего персонала, обладает прогностическим потенциалом и хорошей воспроизводимостью.

§3.1 Основные этапы вычислительного эксперимента

Основными этапами вычислительного эксперимента являются:

• 
  выбор математических моделей объекта и измерительного воздействия;
  
• 
  выбор группы априорно заданных параметров, параметров известных из эксперимента и искомых параметров модели;
  
• 
  выбор метода определения параметров модели и диапазонов их изменения
  
• 
  выбор и реализация алгоритма определения неизвестных параметров;
  
• 
  анализ результатов вычислительного эксперимента и выработка решений по их использованию.
  

Основные этапы вычислительного эксперимента выполняются решением так называемых прямой и обратной задач.

Решение прямой задачи – имитирует проведение натурного эксперимента и состоит в вычислении значений отклика объекта на воздействие измерительного агента в соответствии с заданной моделью объекта и метода измерений. Прямая задача содержит расчётные формулы, описывающие взаимодействие структуры и средства измерения, априорные сведения о свойствах структуры, параметры метода измерения.

Для ясности приведем пример спектрального метода диагностики, основанного на отражении излучения, параметрами метода измерения будут: спектральный диапазон - [λ^L ; λ^U] , шаг изменения дины волны - hλ, угол падения излучения - Θ, поляризация, модуляция и мощности падающего и отражённого излучения I₀ и I, погрешности Δλ и ΔI. Неизвестными параметрами, например, толщина слоя структуры - d_сл и показатель преломления слоя – n_сл, параметры подложки считаются известными. В ходе решения прямой задачи выясняется, какой вид будет иметь спектральная зависимость коэффициента отражения излучения R(λ) от структуры в диапазоне [λ^L ; λ^U] с шагом hλ при заданных показателе преломления- n_сл и толщине слоя - d_сл. и находятся численные значения измеряемых величин.

Анализ получаемых зависимостей типа R(λ)=I(λ)/I₀(λ) следует направить на предварительное выяснение тех особенностей, которые могут негативно повлиять на окончательный результаты измерений. Устранение нежелательных особенностей возможно выбором методов и условий измерений при вариации параметров исследуемой модели объекта. Естественно, что в ходе решения прямой задачи могут быть установлены области высокой чувствительности к определённым параметрам, такой анализ целесообразен, но недостаточен. Вычислительный эксперимент позволяет судить о методе лишь по результатам решения обратной задачи.

Решение обратной задачи – проводит определение неизвестных параметров модели объекта исследования по известным «экспериментальным» значениям выбранного метода измерений. Экспериментальные значения, используемые при решении обратной задачи, могут имитироваться в ходе решения прямой задачи или являться данными реального эксперимента .

Для спектрального метода измерения решение обратной задачи есть нахождение показателя преломления n_сл и толщины слоя d_сл по спектральной зависимости R(λ).

В ходе вычислительного эксперимента могут быть или должны быть введены в расчёты систематические и случайные погрешности измерения откликов и измерительных воздействий при различных вероятностных законах их распределения.

Решив обратную задачу мы получаем искомые значения и можем сопоставить их со значениями, заложенными в расчёты при решении прямой задачи. Мы знаем модель структуры и модель проведения измерений. Вычислительный эксперимент моделирует натурный, но только так, как это было заложено в использованных моделях, алгоритмах и программах решения прямой и обратной задачи.

При проведении натурного эксперимента мы заранее не знаем искомых значений. Задавая различные сочетания искомых параметров n_сл и d_сл, и оценивая расхождение экспериментально измеренных откликов с теми, что рассчитаны в прямой задаче, можно судить об успешности нахождения неизвестных параметров структуры.

Вычислительный эксперимент может дать значительно больше представленного в этом упрощённом примере. Могут быть установлены и количественно определены влияние условий отклонения модели от канонической на результаты определения искомых величин. Может быть установлено влияние погрешностей измерений на результаты, так же как и влияние диапазонов измерений и искомых параметров. Могут быть получены сведения о применимости и эффективности различных способов решения обратной задачи, о корректности задачи и т.п.

Рекомендовать заранее универсальный способ решения обратной задачи не верно. Однако, выработаны некоторые подходы, следование которым позволяет повысить эффективность усилий, направленных на решение обратной задачи, а, следовательно, и на получение данных диагностики.

Далее будет показано, что обратная задача в вычислительном плане, может быть сведена к задаче оптимизации. Поэтому отнесение решаемой обратной задачи к существующему классу оптимизационных задач может дать свои преимущества. А именно, позволит использовать особенности данной задачи с целью построения компактного алгоритма (минимизации затрат машинного времени на решение обратной задачи), максимизации надежности и точности вычислительного метода.

§3.2 Обратная задача как задача оптимизации. Метод наименьших квадратов и минимум функции многих переменных

Решение обратной задачи можно представить решением задачи поиска оптимума. Для начала постараемся записать задачу определения параметров в общем виде, без привязки к конкретному методу, затем для решения обратной задачи применим метод наименьших квадратов и проведем классификацию задач рассматриваемых в данном разделе.

Пусть объектом исследования является простая структура - слой на подложке, метод исследования - спектральная зависимость коэффициента отражения излучения R(λ) от структуры, искомые параметры – показатель преломления слоя - n_сл, показатель поглощения слоя - k_сл и толщина слоя - d_сл, известные параметры объекта – показатель преломления - n_s и показатель поглощения подложки - k_s ; Измерения проводятся в среде с заданными показателем преломления - n_ср, и показателем поглощения - k_ср при нормальных условиях.

Измерения проводятся в выбранном спектральном диапазоне ширины [λ^L ; λ^U], где зависимость оптических констант структуры от длины волны излучения незначима, шаг изменения длины волны – Δλ, параметры поляризации излучения обозначим - Pol. Излучение имеет мощность не достаточную для модификации свойств объекта, излучение не модулируется, угол падения излучения Θ - фиксирован. Существует также функция F - математическое описание реакции (ответа) объекта на измерительное воздействие.

Запишем в векторном виде группы известных постоянных параметров - 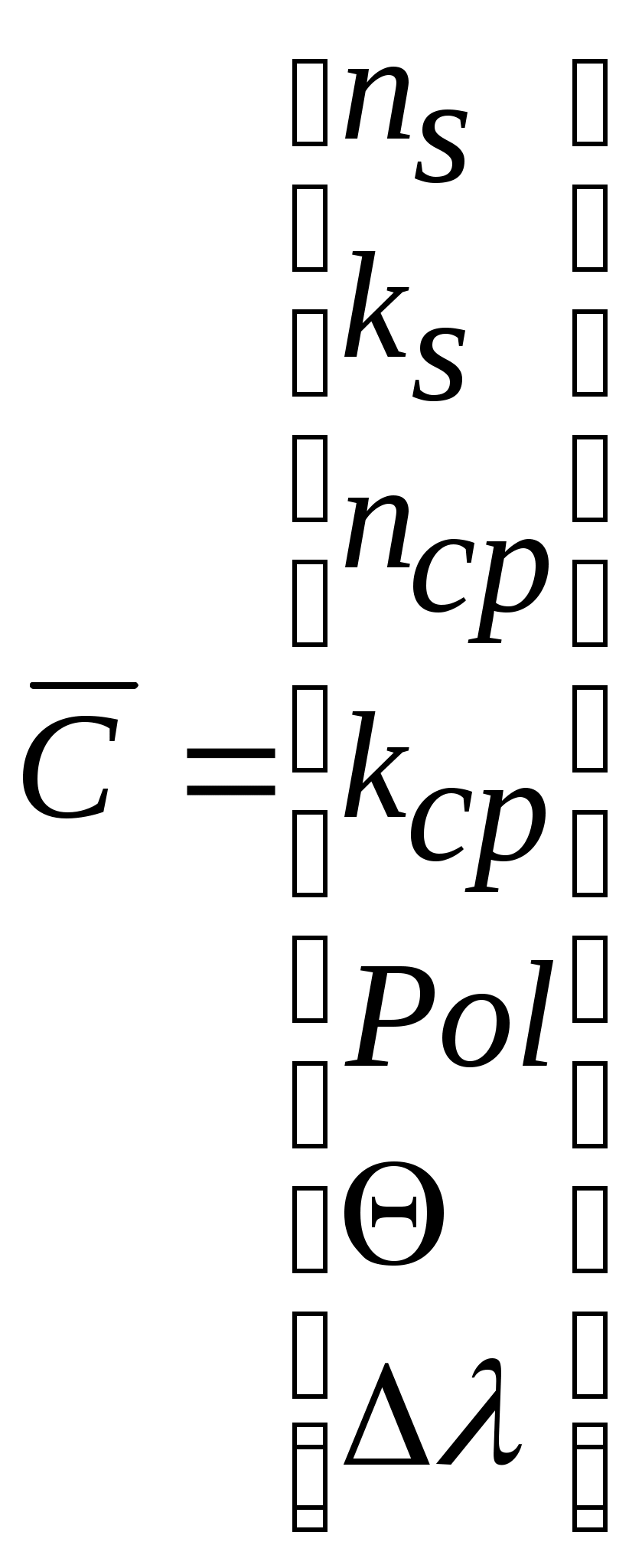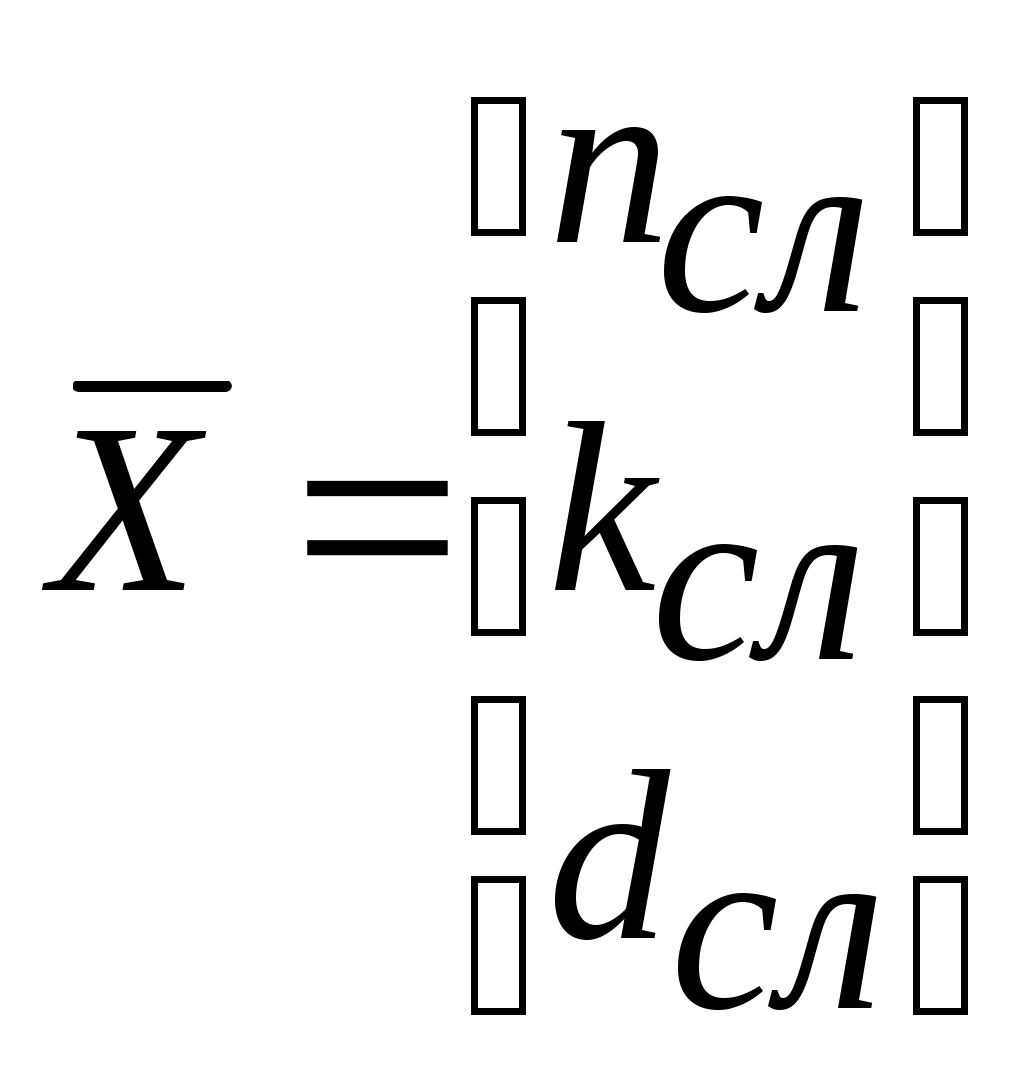, искомых параметров - и параметров измерительного воздействия, варьируемых в ходе измерения - (вектор независимых аргументов).

(3.2.1)

,где L=λ^L - фиксированная верхняя граница диапазона длин волн,

U=λ^U- фиксированная нижняя граница диапазона длин волн,

i= 1.. m – индекс длины волны излучения.

Используя введенные обозначения, связь спектральной зависимости коэффициента отражения и параметров структуры формально можно записать как

(3.2.2)

, где F – математическая модель объекта исследования (структуры). Предполагается, что Х и С не зависят от длины волны.

Решением обратной задачи для описанного случая является нахождение вектора при заданном векторе и измеренной зависимости R(λ). В разобранном случае вектор состоит из n=3 неизвестных параметров структуры - n_сл, k_сл d_сл.

Уравнение (3.2.2) описывает связь определяемых свойств объекта - и его реакции на измерительное воздействие - R(λ). В качестве метода измерения, помимо спектрального, могут быть выбраны любые другие - угловые, спектрально - угловые, поляризационные, вольтамперные, вольт – фарадные, зондовые и т.д.. Для общности рассмотрения левую часть уравнения 3.2.2, как зависимость, соответствующую методу измерения, обозначим - Y_i, где индекс i – обозначает i-e измерительное воздействие. Правая часть 3.2.2 формально остается неизменной, обозначая зависимость ответа на i-e измерительное воздействие от группы постоянных параметров - и группы неизвестных параметров - . В уравнении 3.2.2 вектор можно не указывать явно, помня о его существовании, так как он является вектором постоянных значений в ходе всего метода измерений. В итоге задача запишется

(3.2.3)

В данном разделе примеры всех методов измерений могут быть записаны в виде 3.2.3, поэтому решение обратной задачи для 3.2.3 не ограничивает общности рассмотрения способов решения обратных задач диагностики структур. Если в методе измерения варьируются несколько измерительных воздействий, тогда для каждого i-го значения аргумент t должен быть вектором, здесь и далее будут рассматриваться экспериментальный методы, получающие двухмерные зависимости и потому параметр t будет считаться скалярным.

В этом разделе будем считать функцию F нелинейной, что характерно для приводимых далее примеров задач. Если n есть размерность вектора неизвестных параметров , то при n=1 имеем однопараметровую задачу при n>1 многопараметровую задачу определения свойств объекта. Часто при получении экспериментальной зависимости для нахождения неизвестных параметров применяют метод наименьших квадратов.
Метод наименьших квадратов.

Варьируя параметр измерительного воздействия t_{i ,} i=1..m получают m соответствующих значений отклика структуры - массив экспериментальных данных. Далее требуется определить вектор неизвестных параметров на основе сопоставления сконструированной математической модели структуры и полученных экспериментальных значений . Во многих случаях неизвестные параметры входящие в не выражаются отдельно через другие параметры и все неизвестные компоненты приходится определять одновременно. Такое определение может реализовываться настройкой математической модели на экспериментальные данные подбором компонент вектора неизвестных параметров , эту процедуру относят к задачам идентификации. Настройку можно проводить методом наименьших квадратов (МНК) через введенную функцию S [1]

(3.2.4)

Заключенная в квадратные скобки разность между модельными и экспериментальными значениями в соответствующих точках называется невязкой. Меньшая невязка показывает лучшее приближение точки модельной к точке экспериментальной кривой. Функционал S как сумма квадратов невязок характеризует в целом близость экспериментальной и модельной зависимостей. Получив массив экспериментальных данных, ведут подбор компонент вектора добиваясь минимального значения функционала S. Параметры минимизирующие S представляют собой набор определяемых параметров структуры. Как сумма квадратов невязок S принимает неотрицательные значения, а, учитывая, что экспериментальные значения содержат погрешности и отсутствует возможность абсолютно точно провести «наложение» модельной кривой на экспериментальную, можно утверждать, что S>0. Таким образом, решение обратной задачи определения - вектора неизвестных параметров структуры можно проводить методом наименьших квадратов 3.2.4.

Задачи на нахождение минимума или максимума называют оптимизационными. В нашем случае в качестве целевой функции оптимизационной задачи выступает сумма квадратов невязок . Независимыми переменными являются компоненты вектора . Условия, характеризующие допустимые значения называют ограничениями задачи оптимизации.

Значения компонент вектора неизвестных являются характеристиками реальной структуры (представляя оптические константы, геометрические параметры, фазовый состав и т.п.), следовательно, они могут принимать не все мыслимые значения, а те, что соответствуют некоторым ограничениям. Приводимые далее примеры задач имеют ограничения

(3.2.5)

,где - вектор ограничений наименьших значений , - вектор ограничений наибольших значений .

То есть каждое значение i-го неизвестного параметра лежит в диапазоне, ограниченном L_k и U_k –нижней и верхней границей соответственно. Ограничения вида 3.2.5 называют простыми ограничениями на переменные.

Если целевая функция и/или ограничения являются нелинейными, то задача оптимизации относится к задаче нелинейного программирования, в случае их линейности – задача линейного программирования.

В итоге решение обратной задачи 3.2.3 при использовании МНК сводится к решению задачи на минимум функции 3.2.4. с ограничениями 3.2.5. Ряд алгоритмов, основанных на МНК будут приведены ниже в §3.3.3 и §3.4.2.

Минимум функции многих переменных

Размерность функции S - 3.2.4 зависит от размерности n вектора . Обозначим . Минимизация S есть минимизация функции n переменных. Для нахождения минимума S можно пользоваться значениями самой функции, использовать первые или вторые производные функции.

Первая производная одномерной функции показывает направление и скорость изменения функции. Положительный знак первой производной показывает возрастание функции, отрицательный - убывание, равенство нулю производной соответствует положению максимума или минимума (экстремума). Равенство нулю первой производной является необходимым условием минимума функции одной переменной, достаточным условием является положительный знак её второй производной. Вторая производная характеризует кривизну функции в некоторой точке, для выпуклых участков производная функции отрицательна, для вогнутых – положительна и равна нулю для точек перегиба функции.

Для функции нескольких переменных её первая производная называется градиентом – g и представляет собой вектор частных производных функции по каждой переменной (3.2.6), вторая производная аналогично первой есть совокупность производных от градиента по каждой переменной, которые образуют квадратную матрицу G, называемую матрицей Гессе [1].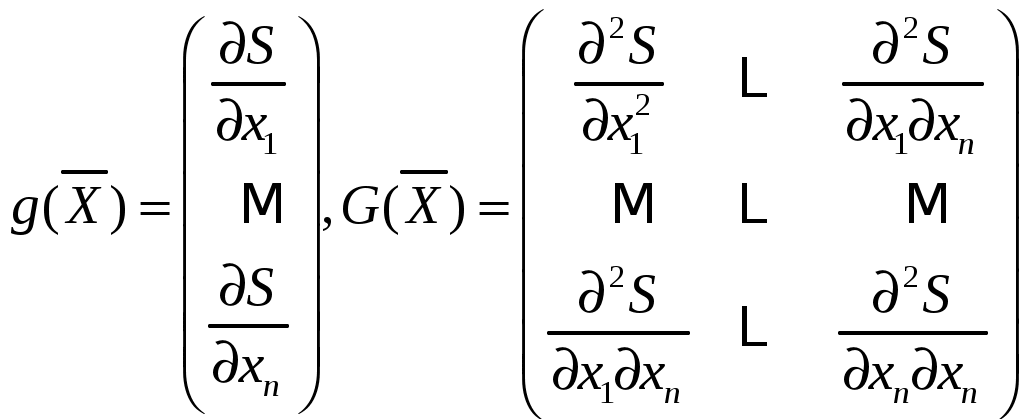

(3.2.6)

Для существования градиента g функция должна быть дифференцируема, то есть в точке и её окрестности должны существовать всё n частных производных, и в они должны быть непрерывны. Аналогично для существования матрицы Гессе, должны существовать и быть непрерывными первые частные производные функции, тогда существуют и вторые частные производные. Класс функций, имеющих непрерывные производные с 1 по k-й обозначают через C^k . Так класс С² есть множество дважды дифференцируемых функций. Класс непрерывно дифференцируемых функций называют «гладкими» функциями. Большинство рассматриваемых здесь обратных задач имеют гладкие целевые функции.

Собственными значениями матрицы G являются числа λ₁,…, λ_n, удовлетворяющие равенству или , где называют собственным вектором, отвечающим собственным значениям λ, I – единичная матрица.

Если все n собственных значений функции положительны, матрица G будет называться положительно определенной, если отрицательны – отрицательно определенной, если неотрицательны – положительно полуопределенной и знаконеопределенной при наличии и положительных и отрицательных собственных значений.

Необходимым условием минимума гладкой функции многих переменных в точке является равенство её градиента нулю в этой точке, достаточным условием является положительная определенность матрицы Гессе. Равенство градиента нулю есть равенство нулю его длины - нормы .

Теперь рассмотрим оптимизационные методы решения обратных задач.