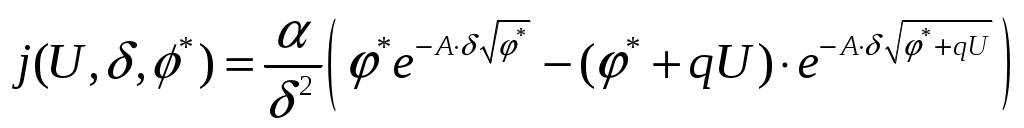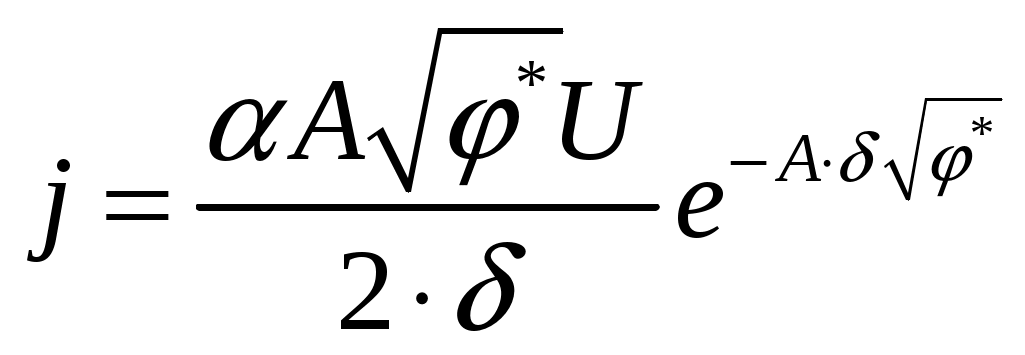Вычислительный эксперимент в методах диагностики микро и наноструктур
 Скачать 2.33 Mb. Скачать 2.33 Mb.
|
|
§3.4 Примеры реализаций вычислительного эксперимента Здесь описаны особенности и приведены примеры обратных задач диагностики микро - и наноструктур. В примерах раздела 3.4.2 обсуждаются возможные способы разрешения встречающихся трудностей. Трудности при решении многопараметровых обратных задач. При решении реальных обратных задач, можно столкнуться с некоторыми трудностями: Наличие нескольких экстремумов минимизируемой функции (многоэкстремальная задача) Установление диапазонов поиска значений определяемых параметров Многопараметровость задачи Слабая чувствительность метода к значениям определяемых параметров и влияние точности измерений на определение параметров Сложность аналитических выражений, связывающих параметры структуры и параметры измерительного воздействие. Сокращение времени решения обратных задач Соответствие модели и объекта. Многоэкстремальность целевой функции Выбирая минимизируемую функцию и приступая к исследованию решений обратной задачи, часто оказывается, что целевая функция имеет несколько минимумов, что означает возможную многозначность решения. Такая задача в общем случае не разрешима методами минимизации, описанными в разделе 3.3, т.к. они применимы для функций с единственным минимумом или для функций рассматриваемых на такой области определения, где он единственен (унимодальные области). В выделенных унимодальных областях методы раздела 3.3 не бесполезны, однако остается вопрос ‑ как выделять области с единственными минимумом не просчитывая значения целевой функции в каждой точке, или как избегать областей где минимума точно не встретиться? Здесь требуется оптимизация работы алгоритма решения обратных задач с целью совершения только необходимых шагов вычислений, что приводит к уменьшению общего времени счета. Если обратная задача решается с целью контроля параметров структур в технологическом процессе, то скорость счета влияет на управляемость, чувствительность регулирования факторов, определяющих функциональные свойства материалов. Универсальные методы, проводящие поиск глобального минимума многоэкстремальной функции без исследования каждого достаточно глубокого минимума пока неизвестны. Выходом из положения может стать использование гибридных методов, сочетающих использование значений самой целевой функции и ее производные. Установление диапазонов поиска значений определяемых параметров Выделение области определения параметров полезно для сокращения области определения целевой функции, приводящее к оптимизации точностных характеристик метода и сокращению времени счета. Здесь также нельзя перечислить набор четких правил выбора допустимых значений параметров, справедливых в любых случаях. Особенности воздействия варьируемых параметров структуры на целевую функцию нужно исследовать отдельно. Многопараметровость задачи Исследование связи целевой функции и определяемых параметров затруднено необходимостью определения одновременно нескольких параметров при единственной целевой функции суммирующей отклики на изменение каждого параметра. Если минимизируемая функция зависит более чем от 2 параметров, то появляется дополнительная сложность, связанная со способом визуализации многомерной функции. Приходится рассматривать проекции такой функции на 3-х мерную плоскость или сечения многомерного объема. С визуализацией 4-х мерных функций помогают современные математические пакеты прикладных программ, позволяющие создавать анимацию, записывая ролик из последовательности трехмерных построений. Мысленно соединяя части анимационного ролика вдоль линии времени можно постараться вообразить 4-х мерную функцию. Другим выходом является построение 4-х мерной функции в трехмерных координатах, где 4-я координата является параметром трехмерной зависимости, выводя несколько поверхностей на один график для улучшения обзора можно настраивать их прозрачность. Цвет поверхности может отображать не только высоту поверхности, как в географических картах, но вместо этого быть отдельной 4-й координатой на 3-х мерной поверхности. Чувствительность метода к значениям определяемых параметров Точность решения обратных задач зависит не только от точности экспериментальных данных и сконструированного вычислительного алгоритма, но и от области в которой находятся значения определяемых параметров, т.е. чувствительность или разрешение метода могут быть неодинаковыми для разных областей параметров. Разрешающую способность метода можно контролировать строя значения решений прямой задачи с использованием созданной сетки параметров из некоторого диапазона. Такие номограммы могут показать области с относительно высоким разрешением - где решения располагаются более редко и распределённо или с низким разрешением - где они располагаются более кучно. Погрешности экспериментальных измерений оказывают влияние на измерения при любых значениях определяемых параметров, однако оно более существенно для областей с низким разрешением. Сложность аналитических выражений Формулы математической модели, описывающие взаимодействие структуры и измерительного воздействия не редко являются довольно громоздкими. При решении прямой и обратной задачи программой регулярно ведется обращение к таким формулам. Одноразовый расчет таких выражений может занимать доли секунды, но при многократном обращении, когда количество итераций исчисляется тысячами, фактор скорости расчета модельных формул становится более значимым. Поэтому нужно стараться записывать функции расчета модельных данных так, что бы минимизировать время их расчета, например, заменяя повторяющиеся выражения громоздкой формулы константами, вычисленными до подстановки в формулу. Если используются методы минимизации с вычислением производных 1 и 2 порядка, то первоначальные формулы модели ещё более усложняются вместе с увеличением времени их обработки. В таких случаях получение дополнительной информации о скорости убывания или кривизне функции может не окупаться временными затратами на вычисления. Выходом может быть использование прямых методов минимизации или методов с конечно-разностной аппроксимацией производных. Сокращение времени решения обратных задач Можно выделить несколько главных факторов определяющих общее время решения обратной задачи: выделение области допустимых значений определяемых параметров; выбор функции и метода минимизации; оптимизация алгоритма, который должен содержать лишь необходимые шаги; учет изученных особенностей конкретной задачи; мощность вычислительной машины. Эффективность любых методов минимизации можно сравнивать по числу обращений к целевой функции, по трудоемкости вычислений функций и их производных, по скорости сходимости, по устойчивости, корректности и надежности получаемых решений. Соответствие модели и объекта Получая решения прямой и обратной задач, нужно помнить о предположениях, в которых была построена математическая модель. При соответствии предположений реальным условиям можно рассчитывать на адекватное представление объекта математической моделью. Математическая модель учитывает существенные особенности объекта и его взаимодействия с окружением, если учтены все существенные особенности, то модель называют полной, иначе – неполной. Сопоставляя значения параметров, определенных различными экспериментальными методами, нужно быть уверенным в адекватности модели объекту во всех используемых методах. Примеры задач и их решение Здесь приведены 4 примера, каждый из которых имеет свою особенность решения прямой или обратной задачи. Пример 1. Определение параметров слоистой структуры методом эллипсометрии. Тип задачи: двухпараметровая, многоэкстремальная, полностью определенная (решаются два уравнения с двумя неизвестными). Особенности решения обратной задачи: прямая подстановка параметров из задаваемого диапазона, решение уточняется сужением диапазона и дроблением шага разбиения. Данный пример является простейшим и иллюстрирует применение МНК для решения обратной задачи. А) Сущность метода Сущность эллипсометрического метода измерений состоит в исследовании изменения состояния поляризации света в результате его отражения от изучаемого объекта. Основное уравнение эллипсометрии имеет вид: Здесь - относительный коэффициент отражения поляризованного излучения, Rp и Rs -амплитудные коэффициенты отражения, характеризующие относительное изменение комплексных амплитуд p- и s-составляющих электрического вектораE при отражении, Ψ-пси и Δ-дельта – эллипсометрические параметры, описывающие эллипс поляризации, δp, δs – фаза p и s- волн соответственно. 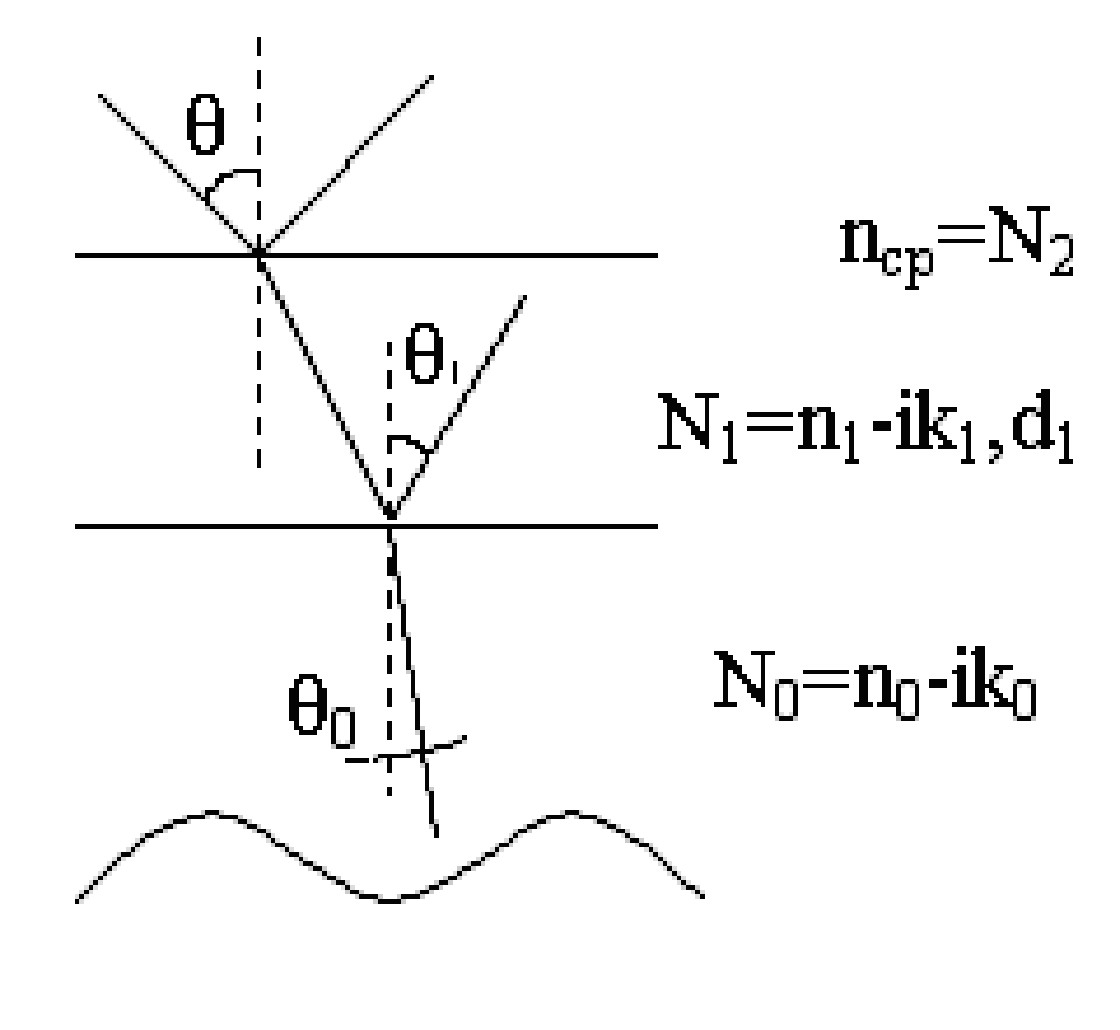 Рисунок 2. Прохождение излучения через систему среда-слой подложка. θ- угол падения излучения, θ1 и θ0 - угол отражения и преломления на границе слой-подложка соответственно. N0, N1, N2- комплексные показатели преломления; n0, n1, nср- показатели преломления, а k0, k1 – показатели поглощения слоя. d1 – толщина слоя.Индекс 0 обозначает параметры подложки, 1- параметры слоя, 2-параметры среды. Для системы среда – слой – подложка (рисунок) основное уравнение эллипсометрии расписывается через коэффициенты Френеля на границах раздела. 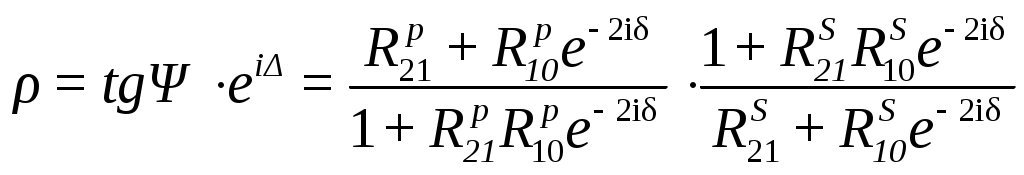 , (3.4.2) , (3.4.2)где 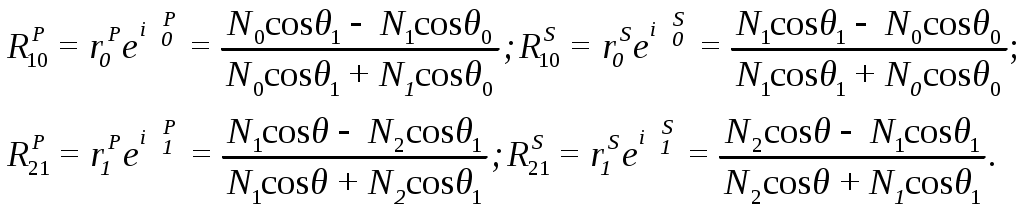 (3.4.4) (3.4.4)λ – длина волны падающего излучения, δ- сдвиг фаз при отражении излучения от слоя. Измерения параметров Ψ и Δ проводятся при постоянных значениях длины волны излучения - λ и угла падения - θ. Б) Прямая задача Определить поляризационные параметры Ψ и Δ при отражении излучения от структуры среда - слой – подложка, если все параметры среды, слоя и подложки считаются известными. В) Обратная задача Для структуры среда- слой – подложка найти параметры слоя n1 и d1 по измеренным поляризационным параметрам Ψ и Δ. Известными фиксированными параметрами считаются N2,N0, k1. Из 3.4.1 получаем выражения для параметров Ψ и Δ В данном примере требуется найти 2 неизвестных параметра по измеренным значениям пси и дельта, которые образуют два уравнения с двумя неизвестными (формула 3.4.5). Если требуется определять более 2-х параметров, то нужно измерять параметры Ψ и Δ при разных углах падения или при разных длинах волн падающего излучения. Г) Решение прямой задачи Внешнюю среду будем считать воздухом с показателем поглощения k2=0. Структура образована не поглощающим слоем, т.е. k1=0. Задаем параметры, считающиеся известными: Угол падения излучения θ=70°. Длина волны падающего излучения λ= 632,8 нм. Показатель преломления окружающей среды n2=1. Показатель преломления слоя n1=1.89 Толщина слоя d1= 650 ангстрем. Показатель преломления подложки n0=3.7 Показатель поглощения подложки k0=0.58 Определяем параметры Ψ и Δ Пользуясь формулами (3.4.2- 3.4.4) подстановкой заданных параметров рассчитываем поляризационные параметры Ψ и Δ по формулам 3.4.5. Для ускорения вычислений полезно сделать следующие замены переменных: 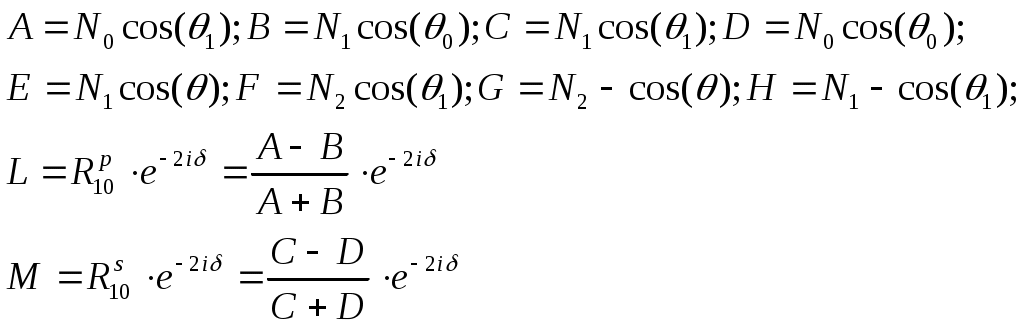 (3.4.6) (3.4.6)Тогда коэффициенты отражения запишутся Основное уравнение эллипсометрии примет вид 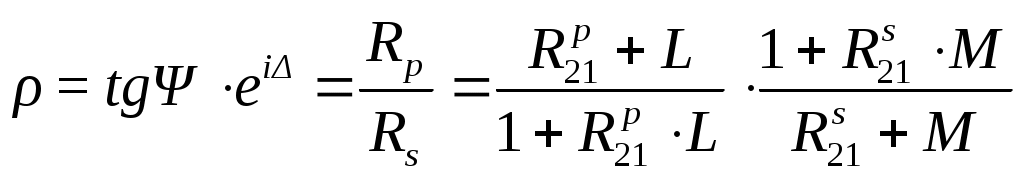 (3.4.8) (3.4.8)Из формул 3.4.5 и 3.4.8 получаем Ψ=34.62 и Δ=53.43. Для исследования чувствительности значений Ψ и Δ к определяемым параметрам структуры можно строить Пси-Дельта номограммы, рассчитывая значения Ψ и Δ для различных сочетаний параметров слоя. 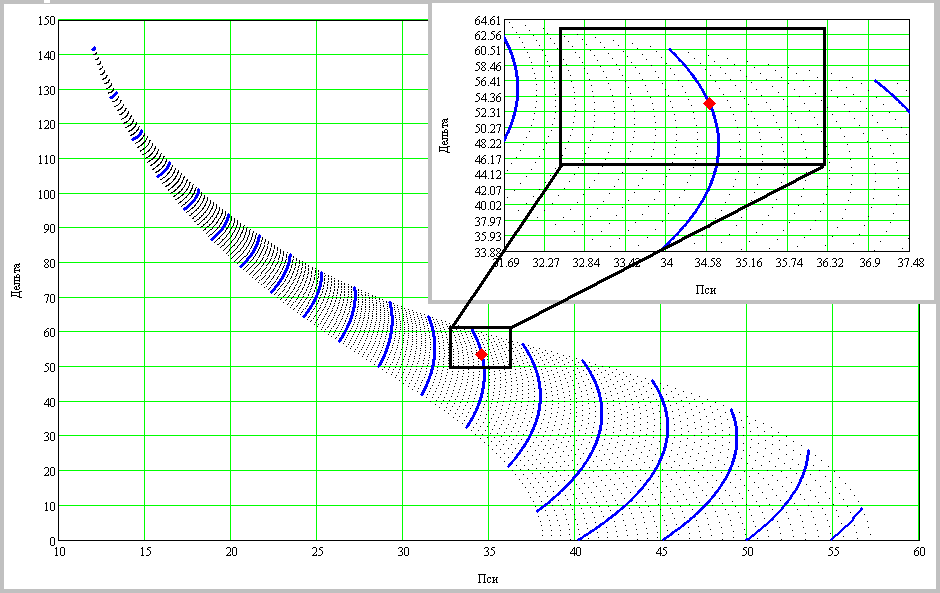 Рисунок 3. Ψ – Δ номограмма. Синие линии соответствуют изменению показателя преломления слоя n1, линии образованные черными точками - изменению толщины слоя d1.Красным ромбом отмечено измеренное значение параметров Ψ и Δ. Номограмма построена для толщин от 50 до 1500 Å с шагом разбиения 5 Å и для показателей преломления слоя от 1.8 до 2.1 с шагом разбиения 0.001. По номограмме видно падение чувствительности к определяемым параметрам при повышении значений Δ и понижении Ψ. Значения Δ и Ψ определяются с некоторой погрешностью метода, поэтому на номограмме корректнее отображать найденные Δ и Ψ не точкой, а областью с доверительными интервалами. Если такая область накладывается более чем на одно значение, то номограмма построена с большим разрешением, чем дает метод в данном случае. Недостатками номограмм является необходимость их построения для каждого типа подложки и большой объем вычислений для широкого диапазона и/или мелкого шага искомых параметров. Д) Решение обратной задачи Для решения обратной задачи используем Ψэксп и Δэксп - экспериментально измеренные значения Ψ и Δ и функцию минимизации где, Ψ(n1,d1) и Δ(n1,d1) – значения поляризационных параметров Ψ и Δ рассчитанные для некоторых параметров слоя n1 и d1. Пользуясь обозначениями раздела 3.2. задачу разбираемого примера можно записать 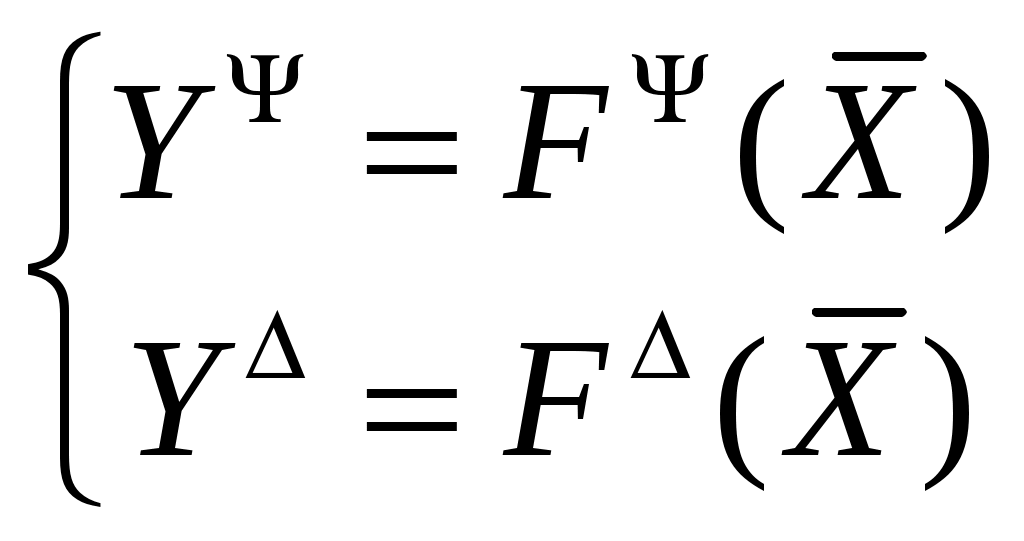 , где YΨ и YΔ - экспериментальные значения Ψ и Δ соответственно, FΨ и FΔ выражения (3.4.5 а) и (3.4.5 б) для модельных значений Ψ и Δ, вектор искомых величин , где YΨ и YΔ - экспериментальные значения Ψ и Δ соответственно, FΨ и FΔ выражения (3.4.5 а) и (3.4.5 б) для модельных значений Ψ и Δ, вектор искомых величинТогда введенные обозначения позволяют переписать функцию минимизации (3.4.9 а) как Экспериментальные значения Ψэксп, и Δэксп измерены с некоторой погрешностью, обусловленные средствами измерения и условиями эксперимента. Погрешность измерения Ψэксп, и Δэксп, а также несоответствие образца и его модели будут вносить искажения в решение обратной задачи. Будем искать минимум (3.4.9) прямой подстановкой эллипсометрических параметров Ψ(n1,d1) и Δ(n1,d1), рассчитанных в прямой задаче для различных пар значений n1, d1. Диапазон значений показателей преломления n1 [1.8, 2.1], шаг Δn1=0.05. Диапазон значений толщины слоя d1 [50,1500] ангстрем, шаг Δd1=50 ангстрем. Построим зависимость S(n1,d1), сопоставлением различных значений S найдем её минимум и соответствующие ему параметры n1min и d1min. Затем выделим новый диапазон поиска параметра n1, который образуется отступом на шаг Δn1 влево и вправо от найденного ранее n1min, т.е. [n1min- Δn1, n1min+ Δn1], с разбиением интервала, например на 5 частей. Аналогично, разобьем интервал возможных толщин слоя [d1min- Δd1, d1min+ Δd1], на 5 частей. В выделенном диапазоне найдем минимум S и соответствующие ему новые значения n1min и d1min. Применяя повторно описанную процедуру к найденным значениям, алгоритм будет осуществлять спуск к минимуму все точнее подбирая наиболее близкие к экспериментальным значения Ψ и Δ и, соответствующие им n1min и d1min (Таблица 1). 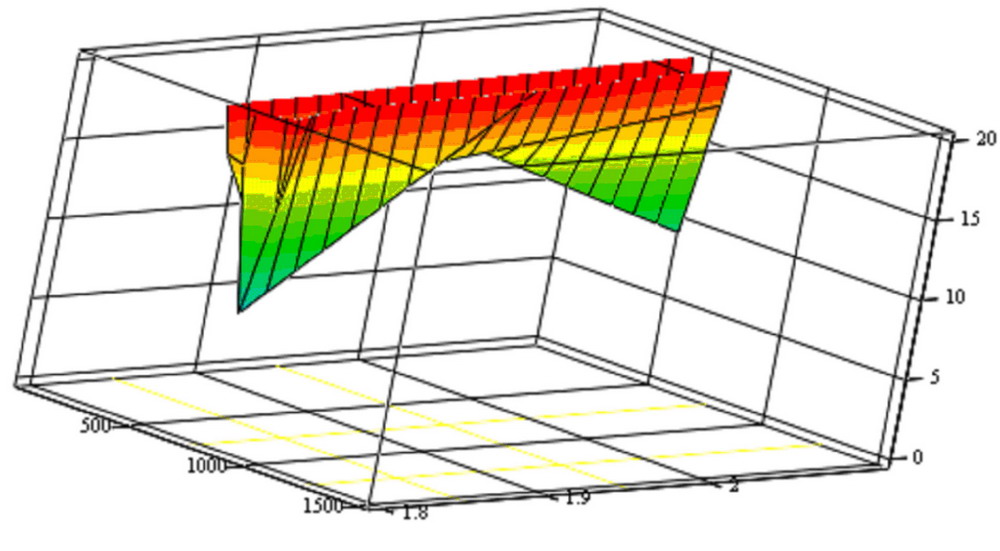 Рисунок 4. Область минимумов функции минимизации S(n1,d1). Таблица 1. Уточнение значений параметров структуры n1=1.89 и d1=650.
Из таблицы видно, что алгоритм постепенно приближается к реальным параметрам слоя n1=1.89 и d1=650 ангстрем, соответствующим значениям, заданным в прямой задаче. Пример 2. Определение параметров слоистой структуры по угловой зависимости коэффициента отражения. Тип задачи: трехпараметровая, многоэкстремальная, переопределенная (решается множество уравнений с тремя неизвестными). Особенности решения обратной задачи: прямая подстановка параметров с равномерным разбиением задаваемого диапазона, решение уточняется дроблением шага разбиения угла. А) Сущность метода Снимается угловая зависимость коэффициента отражения от слоистой структуры. Коэффициент отражения измеряется для числа углов превышающих количество неизвестных параметров структуры. Падающее излучение оптического диапазона поляризовано линейно. Связь между параметрами структуры и коэффициентом отражения устанавливается матричным методом, в котором между слоями вводятся прослойки нулевой толщины с оптическими свойствами внешней среды [6,7]. Такой подход позволяет получить обобщенные формулы для многослойных структур с неограниченным числом слоев. Для N слоя многослойной структуры коэффициент отражения p – поляризованного излучения -RpN икоэффициент отражения s – поляризованного излучения – RsN находятся по формулам (3.4.10) и (3.4.11) 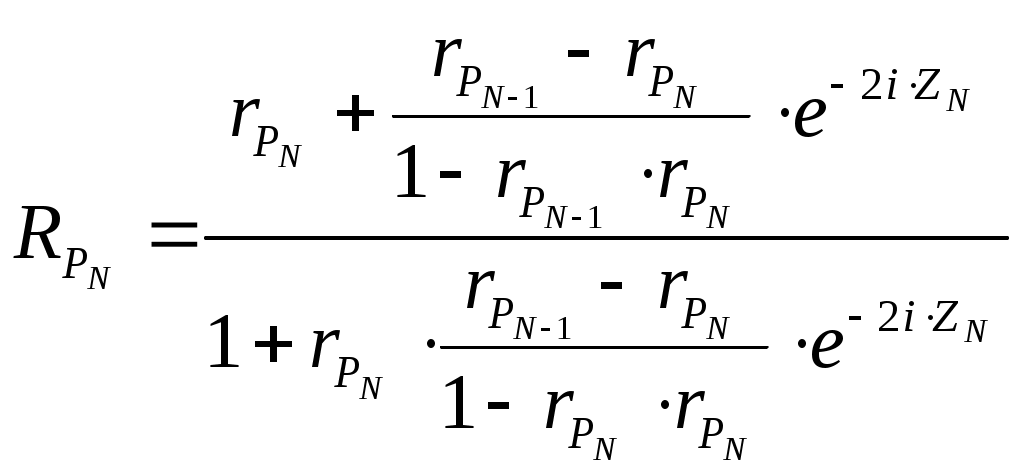 , (3.4.10) , (3.4.10)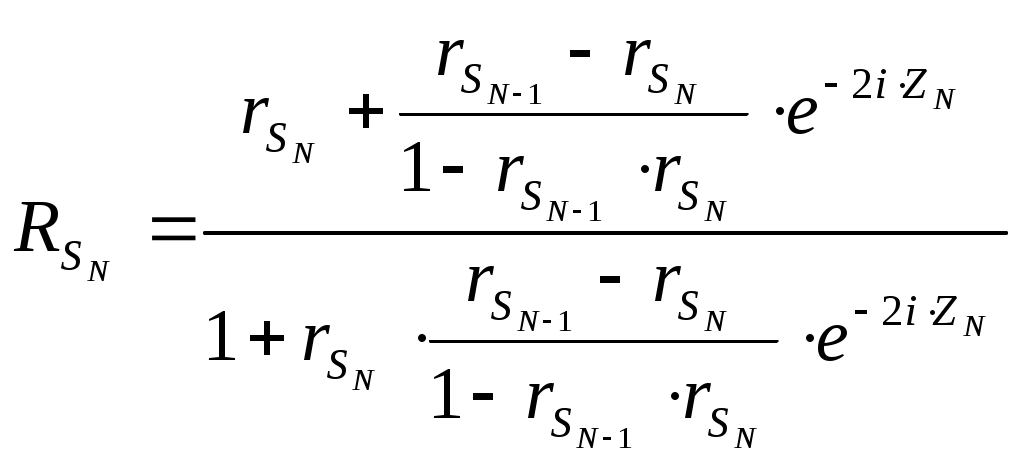 , (3.4.11) , (3.4.11)где Коэффициенты Френеля 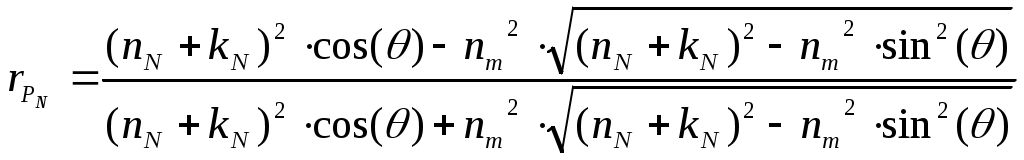 (3.4.12) (3.4.12)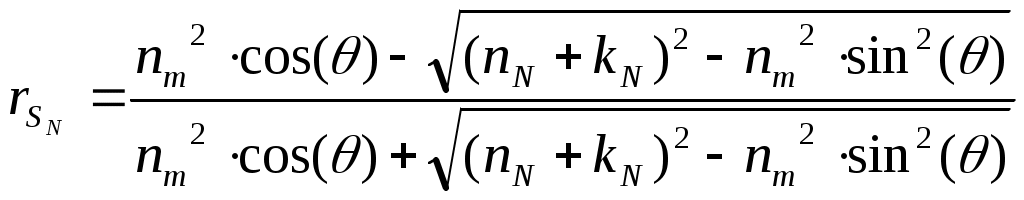 (3.4.13) (3.4.13), где nm-показатель преломления внешней среды.(km=0). nN, kN - показатель преломления и поглощения N слоя соответственно. θ-угол падения излучения.Фазовый сдвиг ZN определяется как 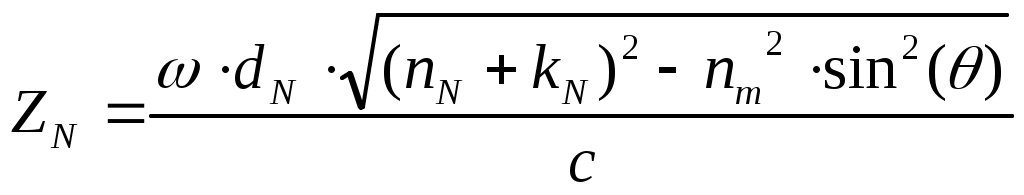 (3.4.14) (3.4.14),где ω-частота падающего излучения, dN-толщина N слоя, с-скорость света. В качестве примера рассмотрим случай падения p-поляризованного излучения на однослойную структуру. С учетом (3.4.10 - 3.4.13) формула энергетического коэффициента отражения Rp для однослойной структуры будет иметь вид 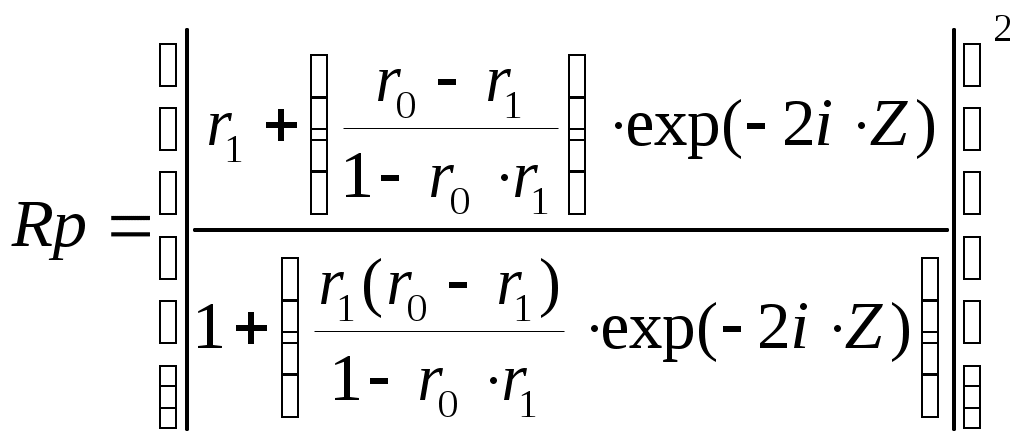 (3.4.15) (3.4.15),где r1- коэффициент Френеля для структуры слой–воздух, r0- коэффициент Френеля для структуры подложка – воздух, Z- фазовый сдвиг при отражении от границы слой-воздух. При заданных длине волны и комплексных показателях преломления подложки и внешней среды угловая зависимость однослойной структуры Rp (Θ) определяется тремя искомыми величинами - dL, nL, kL. Индекс L (от Layer -слой) указывает на отношение параметра к исследуемому слою. Б) Прямая задача Построить угловую зависимость коэффициента отражения Rp(Θ) от слоистой структуры при заданных параметрах структуры, окружающей среды и измерительного воздействия. В) Обратная задача Определить параметры слоистой структуры dL, nL, kL по полученной угловой зависимости коэффициента отражения излучения Rp(Θ). Пользуясь обозначениями раздела 3.2. можно записать Г) Решение прямой задачи Будем исследовать структуру Ag2S слой на SiO2 подложке. Внешняя среда - воздух с показателем поглощения km=0. Задаем параметры, считающиеся известными: Длина волны падающего излучения λ= 632,8 нм. Диапазон углов падения и шаг изменения угла θStart=50°, θEnd=80°, Δθ=1° Показатель преломления окружающей среды nm=1. Показатель преломления слоя nL=2.67. Показатель преломления слоя kL=0.91. Толщина слоя dL= 220 ангстрем. Показатель преломления подложки ns=1.46. Показатель поглощения подложки ks=0. По формулам 3.4.12 и 3.4.15 строим зависимость Rp(Θ). 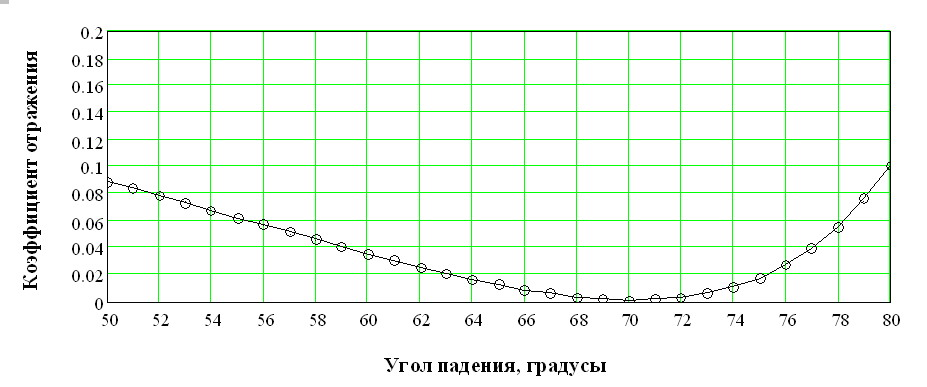 Рисунок 5. Угловая зависимость коэффициента отражения, построенная по вычисленным значениям. Д) Решение обратной задачи Получаем Y- массив моделируемых экспериментальных данных об угловой зависимости коэффициента отражения. Значения содержат погрешности измерений. 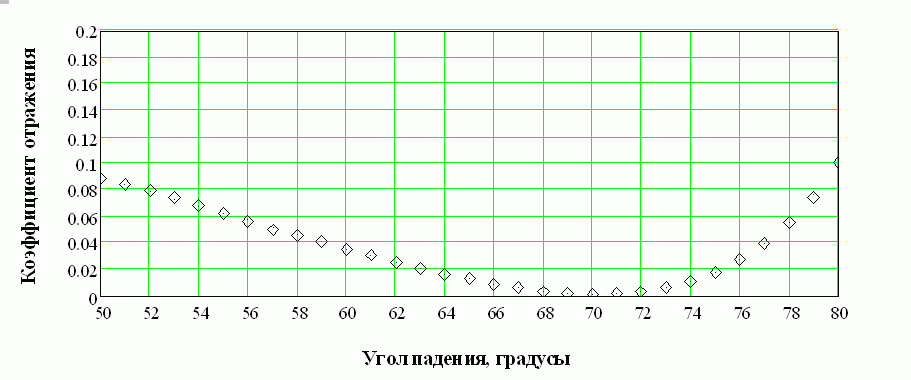 Рисунок 6 Угловая зависимость коэффициента отражения, построенная по моделируемым экспериментальным значениям. Если проводится вычислительный эксперимент, то погрешности экспериментальных значений Yi могут моделироваться добавлением к вычисленным значениям ошибок измерений, распределенных, например, по нормальному закону с заданным среднеквадратическим отклонением σ, которое соответствует прогнозируемым погрешностям эксперимента. Зависимость 3.4.5 построена с добавлением 5 % ошибки к вычисленным данным. Используем функцию минимизации МНК (3.2.4) Особенностью обратной задачи этого примера по сравнению с примером 1 является ее переопределенность, т.к. необходимо найти 3 параметра dL, nL и kL, а по экспериментальным данным возможно составить 30 уравнений – по одному для каждого угла падения. Это дает свободу выбора способа решения обратной задачи. Если в примере 1 решение уточнялось измельчением диапазона искомых параметров, то в этом примере спуск к минимуму S можно осуществлять дроблением шага изменения угла, например, так: 1а) Выбираем широкий диапазон и крупный шаг изменения параметров dL, nL, kL. Это даст уменьшение времени расчета угловой зависимости.; 1б) Рассчитываем 1в) Находим минимум 2а) Сужаем диапазон поиска параметров, отступая от каждого из параметров 2б) Рассчитываем 2в) Находим минимум *) и.т.д. до достижения требуемого значения минимума Расчет Проведем решение по описанной схеме. Будем сужать диапазон поиска параметров dL, nL и kL, уменьшать шаг разбиения диапазона и увеличивать количество рассматриваемых точек угловой зависимости. Условия поиска и результаты приведены в Таблице 2. 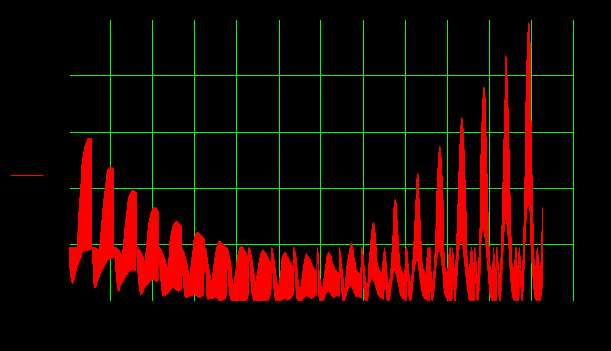 Рисунок 7. Функция Таблица 2. Поиск параметров структуры Ag2S на SiO2 с истинными параметрами слоя dL= 0.0220 мкм, nL=2.67, kL=0.91. Погрешность моделируемых экспериментальных значений Rp(Θ) составляет 5%.
Данные таблицы показывают, что даже при внесении 5% погрешности в экспериментальные значения решение обратной трехпараметровой задачи дает значения параметров с небольшим отличием от истинных значений. Для толщины слоя dL оно составляет 0.0005 мкм, для показателя преломления nL – 0.01 и для показателя поглощения kL- 0.008. Находить параметры также можно с использованием сочетаний,например, по три точки угловой зависимости из 10 выбранных точек. В таком случае образуется 120 сочетаний по три точки в каждом, решается обратная задача для каждого сочетания, полученные результаты усредняются. Пример 3. Определение потенциального рельефа и работы выхода методом туннельной зондовой микроскопии. Тип задачи: двухпараметровая, переопределенная. Особенности решения прямой задачи: для исключения мультипликативной и аддитивной погрешностей используются не прямые данные эксперимента, а образованные из них функции, которые включают измеренные производные при разных управляющих параметрах экспериментальной установки. А) Сущность метода Экспериментально метод реализуется с использованием сканирующего туннельного микроскопа (СТМ), который измеряет потенциальный рельеф поверхности, характеризующий её геометрический рельеф. Работа СТМ основана на явлении туннелирования электронов через узкий потенциальный барьер между металлическим зондом и проводящим образцом во внешнем электрическом поле. При подведении зонда к поверхности образца на расстояния в несколько ангстрем образуется туннельно-прозрачный потенциальный барьер, величина которого определяется, значениями работы выхода электронов из материала зонда φP и образца φS. При качественном рассмотрении барьер можно считать прямоугольным с эффективной высотой, равной средней работе выхода материалов по формуле
При приложении к туннельному контакту разности потенциалов U между зондом и образцом появляется туннельный ток. В процессе туннелирования участвуют, в основном, электроны с энергией в окрестности уровня Ферми EF. В случае контакта двух металлов выражение для плотности туннельного тока (в одномерном приближении) примет вид
где q – заряд электрона; β – коэффициент равный 23/24; δ – туннельный зазор между поверхностью и зондом, h- постоянная Планка, U – напряжение смещения, прикладываемое между зондом и образцом.
При таких напряжениях справедливо соотношение (3.4.17) для φ*, а ширина барьера ΔZ соответствует расстоянию между кончиком зонда и поверхностью образца - δ. Если напряжение смещения сопоставимо с работой выхода, то формула для φ* запишется
В работах [8, 9] описан метод определения контактной разности потенциалов на основе гармонической модуляции туннельного зазора. Для неоднородных образцов туннельный ток зависит не только от расстояния зонд - образец, но и от значения локальной работы выхода электронов на зондируемом участке поверхности. Предположим, что проводятся измерения на СТМ в режиме постоянного тока, когда при движении зонда над образцом туннельный ток поддерживается постоянным за счет перемещения Z - двигателя зонда. При таком режиме расстояние между зондом и поверхностью образца (туннельный промежуток δ) должно сохраняться постоянным, тогда перемещение зонда будет отражать изменение рельефа поверхности. Это верно в предположении постоянства работы выхода электронов с поверхности вещества. Если образец имеет неоднородное распределение работы выхода φ, то поддержание постоянного туннельного тока не гарантирует постоянство туннельного промежутка, а следовательно рельеф поверхности будет определяться с погрешностями. Для получения информации о распределении работы выхода применяется метод модуляции расстояния зонд - образец ∆Z. В процессе сканирования к управляющему напряжению пьезоэлемента Z-электрода сканера добавляется переменное напряжение с внешнего генератора на частоте ω и амплитудой Zm. Это приводит к тому, что расстояние зонд - образец становится модулированным с частотой ω, изменение Z координаты зонда описывается формулой
где Z0- Z координата зонда при постоянном напряжении на пьезоэлементе. Частота ω выбирается выше частоты полосы пропускания петли обратной связи для того, чтобы система обратной связи не могла отрабатывать накладываемые колебания зонда. Амплитуда колебаний пьезоэлемента Zm выбирается достаточно малой, чтобы возмущения туннельного промежутка также были малыми. При этом необходимо, чтобы значение напряжения смещения удовлетворяло неравенству Uq<<φ*. При постоянном напряжении смещения, с учетом 3.4.19 и принятых выше условий выражение для туннельного тока, модулированного на частоте ω запишется
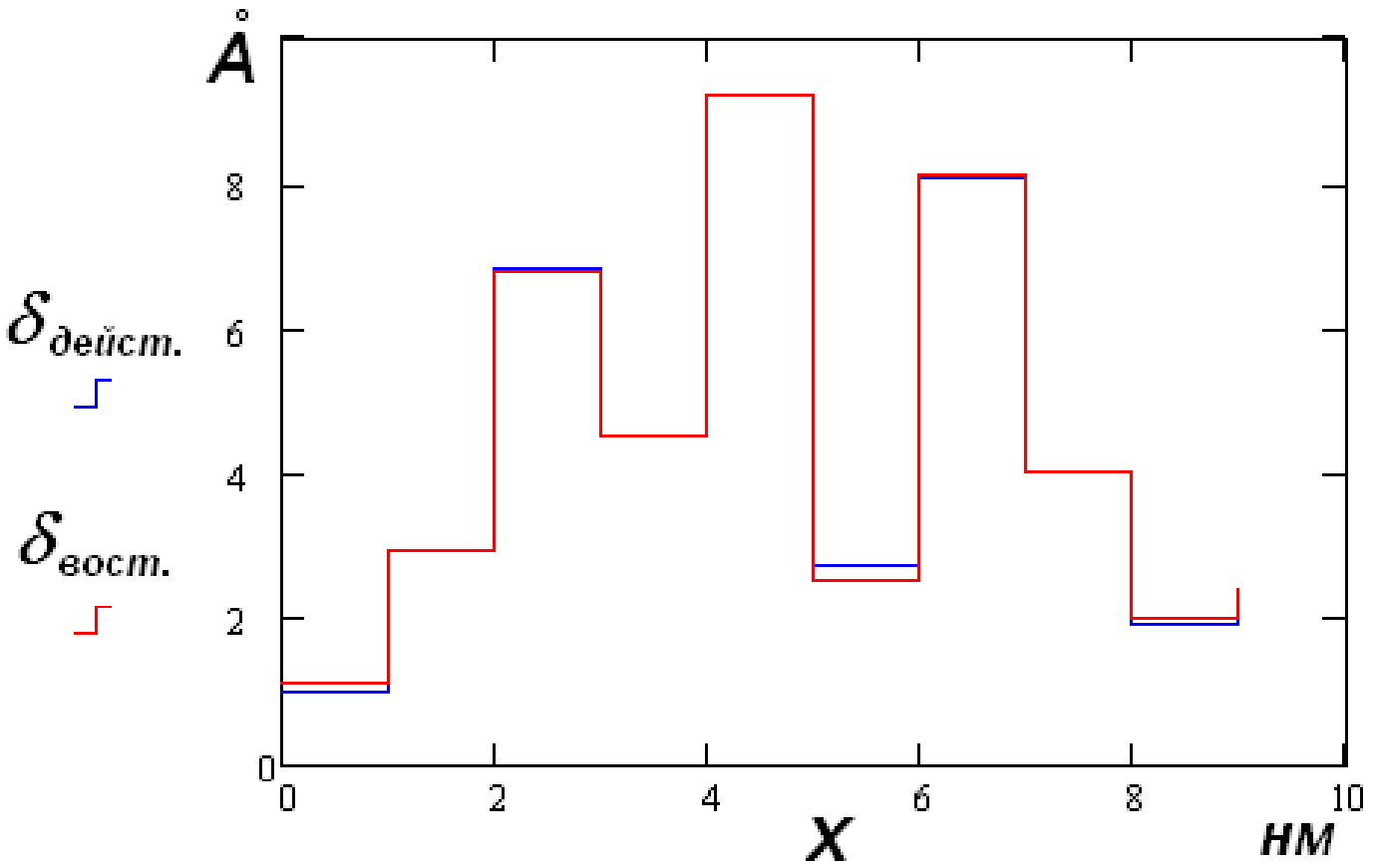
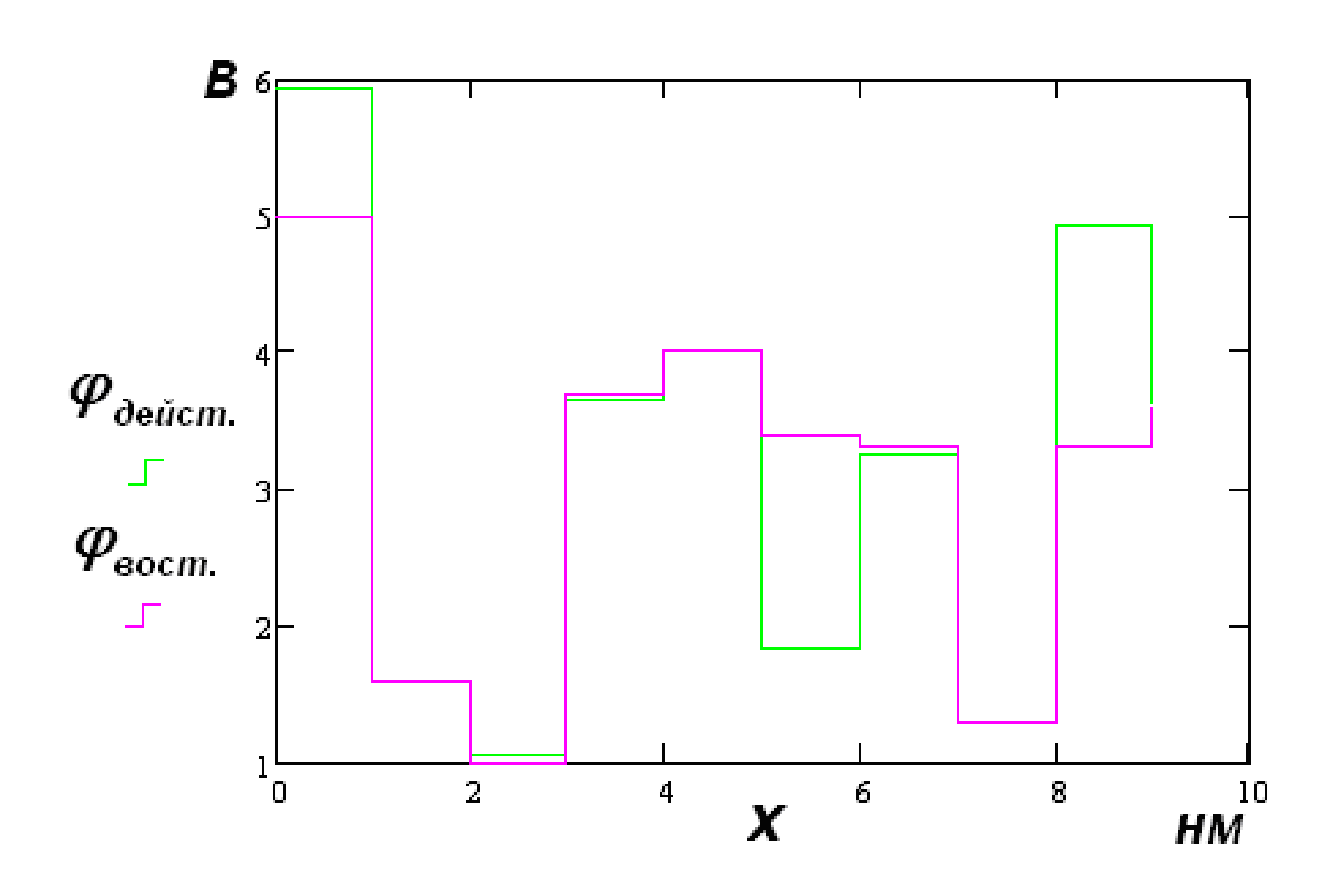
где I0- постоянная составляющая туннельного тока. Это позволяет раздельно определять туннельный промежуток и работу выхода в каждой исследуемой точке поверхности. Поддерживая в процессе сканирования ток I0 постоянным, отслеживаем движение зонда по координате Z и таким образом получаем данные об экспериментальном рельефе Z = f(x,y). Одновременно по малой амплитуде высокочастотных колебаний туннельного тока получаем данные о распределении локальной работы выхода φ(x,y) на исследуемом участке поверхности. Истинный рельеф поверхности восстанавливается по экспериментальному рельефу с учетом определенных значений работы выхода. Б) Прямая задача По значениям работы выхода – φ и туннельного промежутка - δ, заданным для каждой исследуемой точки поверхности образца, определить fU - производную туннельного тока по напряжению смещения и fδ – производную туннельного тока по туннельному зазору при трех различных напряжениях смещения U1, U2, U3. С использованием рассчитанных fδ и fU строятся новые функции D1 и D2, устраняющие возможные мультипликативные и аддитивные погрешности. В) Обратная задача По измеренным производным fU и fδ для трех различных напряжений смещения U1, U2 и U3 определить работу выхода φ и экспериментальный туннельный промежуток δ в каждой исследуемой точке. Относительное изменение туннельного промежутка отражает рельеф исследуемой поверхности. Г) Решение прямой задачи Задаются значения δ и φ для каждой исследуемой точки поверхности образца. Производные рассчитываются по формулам 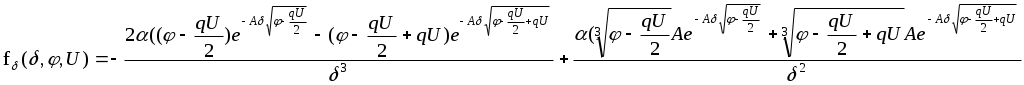 В каждой точке измеряются величины производных при различных напряжениях на зонде U1, U2, U3. Влияние аддитивных и мультипликативных погрешностей исключается введением относительных величин разностей значений fU и fδ, для различных значений напряжений, описываемых соотношениями 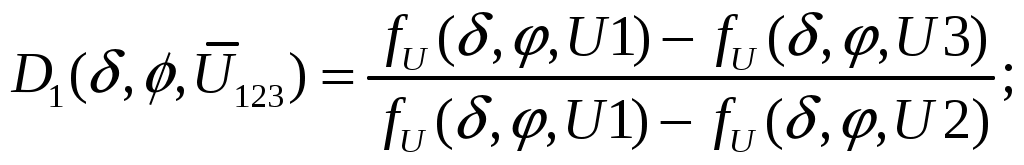 (3.4.23) (3.4.23)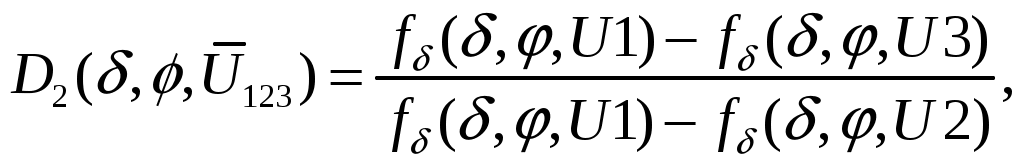 (3.4.24) (3.4.24)где Д) Решение обратной задачи Для построения экспериментальных D1 и D2 определяются значения производных fU и fδ при трех напряжениях смещения U1, U2, U3. Как и в примерах 1, 2, используем обозначения раздела 3.2 и приведем задачу нахождения параметров к виду 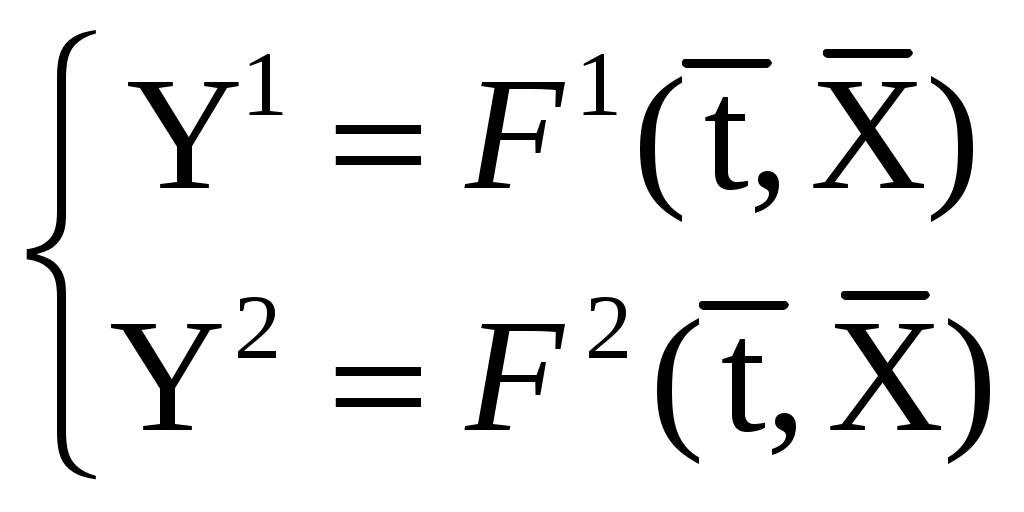
Рисунок 8. Действительный и восстановленный туннельный зазор (а), работа выхода (б) для 10 зондируемых точек поверхности. Вектор Возьмем функцию минимизации аналогичную функции (3.4.9) в примере 1, тогда целевая функция запишется: Методом минимизации невязки определяются искомые значения туннельного зазора δ и работы выхода φ. По найденным значениям строится действительный рельеф поверхности (рисунок 8). |