Вычислительный эксперимент в методах диагностики микро и наноструктур

• Название: Вычислительный эксперимент в методах диагностики микро и наноструктур
• Дата: 01.07.2022
• Размер: 2.33 Mb.
• Имя файла: razdel_3.doc
• Тип: Документы; #622327
• страница: 2 из 6

§3.3 Решение обратной задачи методами поиска минимума функции  многих переменных

Решение обратной задачи

Требуется решить обратную многопараметровую задачу определения n параметров структуры, применяя метод наименьших квадратов (МНК) для уравнения 3.2.4, с линейными ограничениями 3.2.5.

Искомые параметры, соответствуют минимуму суммы квадратов невязок модельных данных с экспериментальными. Если функция имеет на некотором интервале единственный минимум, то такая функция называется унимодальной. Решение задачи определения параметров МНК будет однозначным, если выделен отрезок локализации , ε – радиус интервала неопределенности, где функция является унимодальной.

Чаще всего имеет несколько локальных минимумов и параметры, определенные МНК, могут иметь ошибочные значения. Для наилучшего решения обратной задачи необходимо нахождение глобального минимума.

Задача определения параметров структуры сводится к минимизации многоэкстремальной функции нескольких переменных. На решение обратной задачи накладываются линейные ограничения 3.2.5, поэтому имеем случай условной минимизации.

Решение обратной задачи методом наименьших квадратов можно проводить, решая систему нелинейных уравнений. Если известно, что необходимым условием минимума является равенство нулю градиента функции в точке минимума 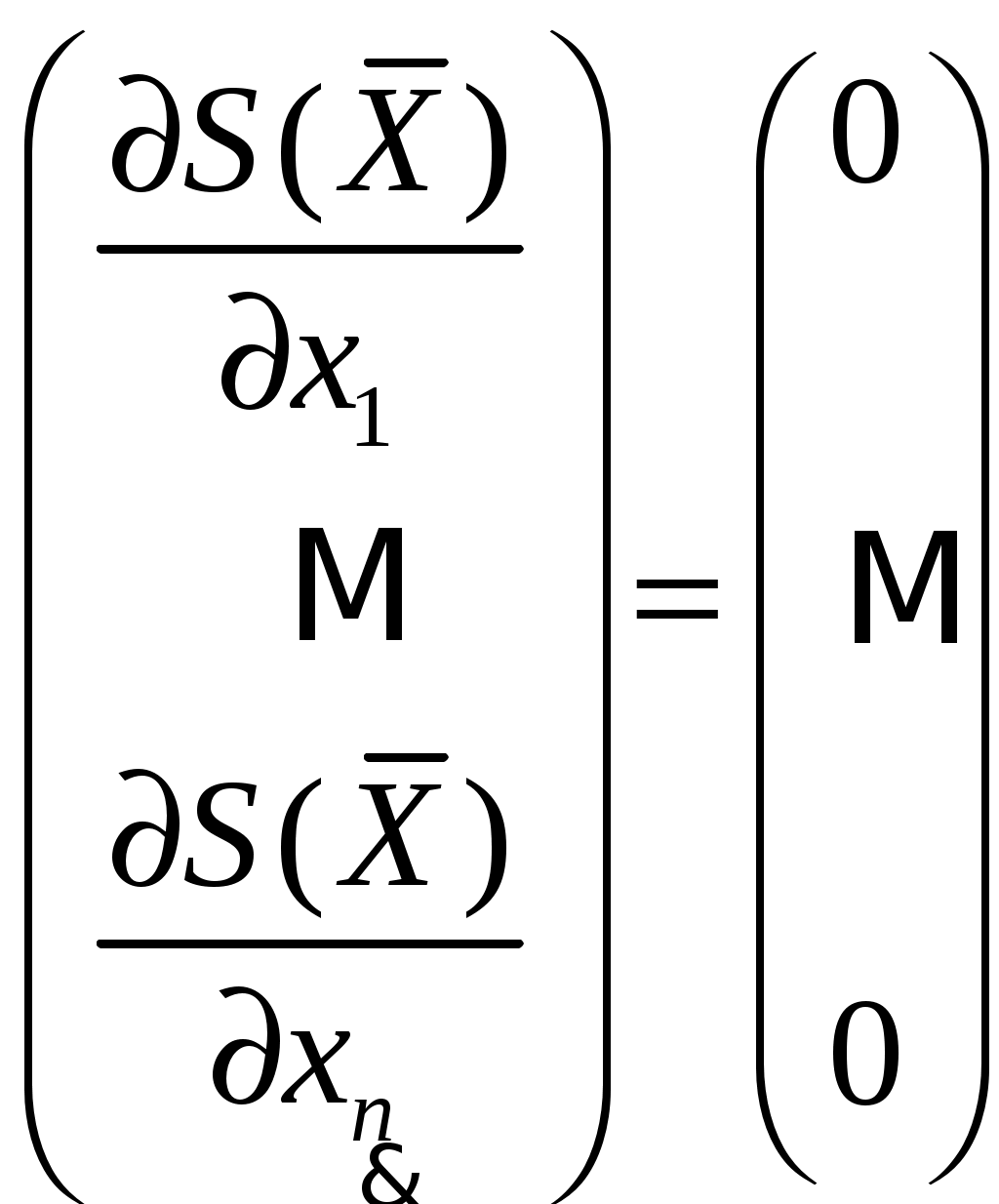, то корень векторного уравнения

(3.3.1)

дает комплекс неизвестных параметров. Чаще всего система 3.2.6 имеет несколько решений и численными методами, например, градиентными, нужное решение находится успешно в том случае, если задана точка начального приближения, на участке близком к истинному корню – глобальному минимуму S. Однако в реальных задачах указать малую окрестность, содержащую минимум, затруднительно. Ситуация усложняется, если на пути от точки приближения к глобальному минимуму встречаются дополнительные локальные минимумы.

Несколько отличающимся, но близким по смыслу является решение обратной задачи методом наименьших квадратов с использованием алгоритмов поиска минимума функций многих переменных.
Алгоритмы поиска минимума функции многих переменных

Информацию о приближении к минимуму дает сопоставление значений целевой функции в пробных точках, позволяя последовательно сокращать интервал неопределенности положения минимума. Вычисление первых и вторых производных дополняет алгоритм минимизации информацией о поведении функции в данной точке и её окрестностях, позволяя делать более широкие шаги к минимуму целевой функции. В любом случае в процессе минимизации нужно стараться использовать всю доступную информацию о функции, соотнося «затраты» на дополнительные вычисления и ценность получаемых из них сведений.

Общей чертой большинства итерационных алгоритмов минимизации является требование, чтобы на каждом последующем шаге итерации целевая функция убывала S_k+1 < S_k . Методы, удовлетворяющие такому требованию, называются методами спуска. Все описанные ниже алгоритмы относятся к методам спуска и отличаются способами выбора направления и шага спуска.

Алгоритмы минимизации можно поделить на категории в зависимости от использования в них значений производных:

а) методы второго порядка – с вычислением 2-х производных целевой функции;

б) методы первого порядка – с вычислением 1-х производных;

в) методы нулевого порядка – без вычисления производных.
Обзорно опишем суть методов а, б.

а) К методам второго порядка относятся метод Ньютона и его модификации [1]. Метод Ньютона основан на квадратичной аппроксимации целевой функции.[1. стр. 141]. Располагая первыми и вторыми производными целевой функции S (гладкая функция), в качестве её квадратичной модели можно взять сумму первых трех членов тейлоровского разложения в окрестности текущей точки , т.е. воспользоваться приближенным равенством вида

(3.3.2)

здесь -направление движения, верхний индекс Т обозначает транспонирование вектора, g_k и G_k – градиент и матрица Гессе в точке .

Минимум правой части 3.3.2 достигается при векторе минимизирующем квадратичную форму

(3.3.3)
Будучи стационарной точкой , этот вектор должен удовлетворять равенству

(3.3.4)

Алгоритм минимизации в котором направление p_k определяется системой 3.3.4, называется методом Ньютона, а направление, дающее решение системы называют ньютоновским направлением.

б) К основным методам первого порядка относятся: градиентные методы, методы сопряженных градиентов, квазиньютоновские методы и аналоги методов 2 порядка с конечно-разностными аппроксимациями 2-х производных.

Градиентный метод основан на том, что градиент функции указывает направление максимального роста функции, а антиградиен – направление наискорейшего движения к минимуму. Если задана k-я точка приближения, то на каждой последующей итерации шаг определяется из условия



(3.3.5)

где p_k – направление, определяемое антиградиентом

- величина шага в направлении p_k.

Метод выбора шага определяет вариант градиентного метода [5].

Ньютоновские методы минимизации, вычисляя матрицу Гессе, используют информацию о кривизне функции. Квазиньютоновские методы опираются на возможность аппроксимации кривизны нелинейной функции без явного формирования ее матрицы Гессе. Данные относительно кривизны целевой функции определяются на основе наблюдений за изменением градиента g во время итераций спуска [1].

Метод сопряженных градиентов использует понятие сопряженное направление, которое четко определено лишь для квадратичной функции [5]. Ненулевые векторы являются взаимно сопряженными относительно симметричной матрицы A квадратичной функции , если , для всех . Методом сопряженных градиентов для квадратичной функции называют метод, в котором сопряженные направления строятся по правилу

(3.3.6)

,где β_k- числовой коэффициент.

Для произвольной гладкой функции коэффициент β_k дается как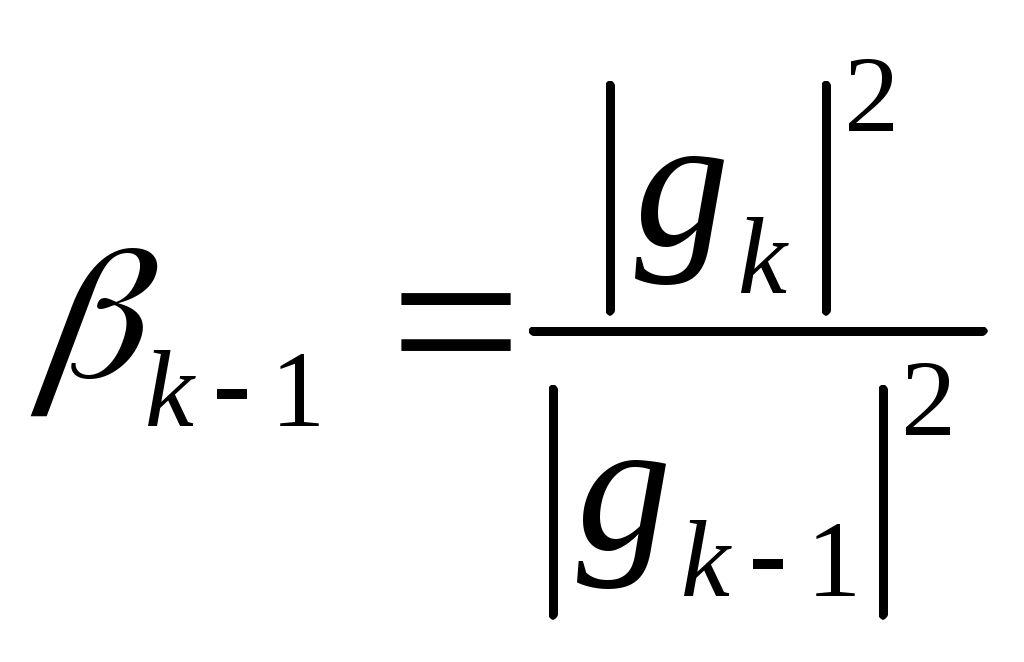

или (3.3.7)

Минимизацию целевой функции производят в соответствии с формулой (3.3.8)

,где направления вычисляют по формуле 3.3.6 с использованием 3.3.7, а шаг αk >0 вычисляется из решения задачи одномерной минимизации функции .

Геометрический смысл метода сопряженных градиентов состоит в следующем (рисунок 1) [10]. Из заданной начальной точки х(0) осуществляется спуск в направлении р(0) = -f'(x(0)). В точке х(1) определяется вектор-градиент f'(x (1)). Поскольку х(1) является точкой минимума функции в направлении р(0), то f’(х(1)) ортогонален вектору р(0). Затем отыскивается вектор р (1), G-сопряженный к р (0) (G - матрица Гессе.) . Далее отыскивается минимум функции вдоль направления р(1) и т. д.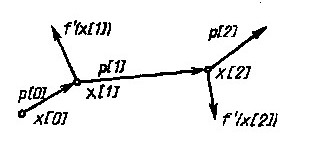



Рисунок 1. Траектория спуска в методе сопряженных градиентов

Методы сопряженных направлений являются одними из наиболее эффективных для решения задач минимизации. Однако следует отметить, что они чувствительны к ошибкам, возникающим в процессе счета, и для большого числа переменных не являются оптимальными [10].

в) К методам нулевого порядка относятся: прямой поиск, метод покоординатного спуска, метод деформируемого многогранника, методы Розенброка и Дэвиса, Свенна, Кемпи, с которыми можно ознакомиться в [1,3,4,5]. А также методы, в основу которых положены алгоритмы с вычислением производных, но сами производные заменяются конечно-разностными аппроксимациями.

Для минимизации задачи о наименьших квадратах 3.2.4 выгодно использовать алгоритмы, специально разработанные для таких задач. В специальных методах решения задачи МНК учитывается особая структура градиента и матрицы Гессе функции .

Некоторые специальные методы решения задач о наименьших квадратах

Опишем существо специальных методов минимизации задачи МНК - метод Гаусса-Ньютона, Левенберга – Маркардта и универсальный квазиньютоновский метод.

Прежде покажем, в чем особенность градиента и матрицы Гессе задачи МНК.

Обозначим невязку в 3.2.4 как , и пу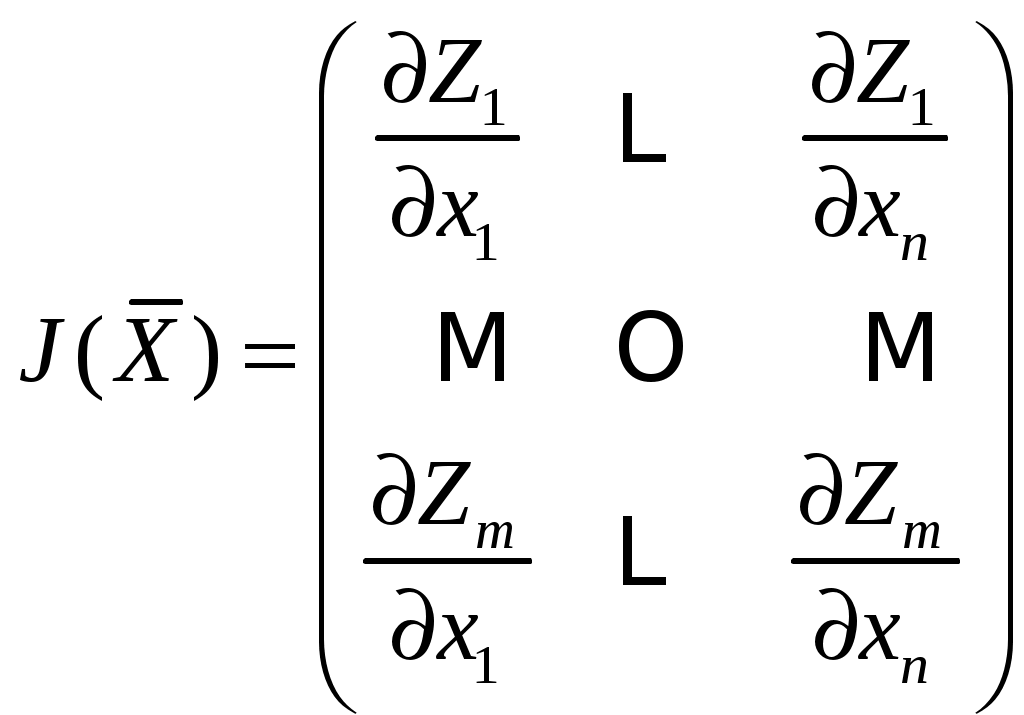сть - матрица Гессе для , тогда, вычислив градиент и матрицу Гессе функции S в 3.2.4, можно убедиться, что они формально запишутся [1]

(3.3.9 а)

(3.3.9 б)
, где ,

Здесь – матрица Якоби функции , - транспонированная матрица , G_i- матрица Гессе для

Заметим, что матрица Гессе G вычисляется с использованием первых и вторых производных . В окрестности точки минимума невязки становятся малыми и второе слагаемое в (3.3.9 б) также мало по сравнению с первым. Специальные алгоритмы решения задачи МНК опираются на преобладании первого слагаемого над вторым, что позволяет приближенно вычислять матрицу Гессе в окрестности точки минимума лишь по первым производным функции , хотя, по сути, используются методы второго порядка.
Метод Гаусса - Ньютона.

Обозначим через текущую оценку решения задачи минимизации функции 3.2.4, нижний индекс k будет обозначать её принадлежность к .

Тогда ньютоновская система 3.3.4 в силу 3.3.9 примет вид [1]



(3.3.10)

При приближении к оптимуму невязки Z_k будут близки к нулю и матрица Q_k также будет приближаться к нулевой. Значит ньютоновское направление можно аппроксимировать решением системы

(3.3.11)

Решение 3.3.11 представляет собой оптимальный вектор в одномерной задаче о наименьших квадратах по нахождению минимума суммы

(3.3.12)

, если матрица J_k имеет линейно независимые столбцы (полный столбцовый ранг), то вектор определен однозначно, при этом его можно обозначить как p_GN. Если линейная независимость столбцов J_k нарушается, то задача 3.3.12 будет иметь целое многообразие решений [1]. Метод минимизации, в котором p_GN используется в качестве направления поиска, называется методом Гаусса-Ньютона. Когда Q_k близка к нулю, направление Гаусса-Ньютона p_GN мало отличается от ньютоновского направления p_N. Метод Гаусса-Ньютона может достигать квадратичной скорости сходимости, хотя при расчете p_GN учитываются только первые производные.
Метод Левенберга - Маркардта.

Альтернативой методу Гаусса-Ньютона является метод Левенберга-Маркардта. В нем направление поиска определяется как решение системы уравнений вида

(3.3.13)

,где λ_k - некоторое неотрицательное число, I – единичная матрица. В этом методе шаг p_k всегда полагается единичным, т.е. очередной точкой x_k+1 будет x_k+ p_k. Можно показать, что p_k – решение задачи на условный минимум
, при ограничении (3.3.14)
где Δ- параметр связанный с λ_k. Монотонное убывание минимизируемой функции в методе Левенберга – Маркардта достигается за счет подбора «хороших» значений λ_k. При λ_k равном нулю, p_k будет направлением Гаусса-Ньютона. Когда λ_k стремиться к бесконечности, p_k стремиться к нулю и в пределе становится параллельным антиградиенту, следовательно, выбрав λ_k достаточно большим можно обеспечить выполнение неравенства для суммы квадратов невязок .

Пусть p_LM- решение системы 3.3.13, при каких-то x_k и положительных λ_k. Если для матрицы J_k условие линейной независимости столбцов не выполняется, то независимо от величин Q_k и λ_k направление p_LM будет близко к направлению p_GN в методе Гаусса – Ньютона.

Таким образом, и в методе Гаусса – Ньютона и в методе Левенберга - Маркардта пользуются предположением о доминирующей роли слагаемого в 3.3.9 б, исходя из чего матрицей Q предлагается пренебречь. Однако , метод Левенберга – Маркардта более устойчив чем метод Гаусса – Ньютона в отношении выполнения условия линейной независимости столбцов J_k.

Квазиньютоновский метод.

(Метод переменной метрики или метод Девидона).

Квазиньютоновский метод использует сведения о кривизне функции, которые накапливаются в ходе наблюдения за значениями градиента в процессе итераций спуска к минимуму.

Разложим градиент в ряд Тейлора в окрестности по степеням (шаг из точки ) .

Тогда оценка кривизны целевой функции S вдоль , т.е. произведение запишется

(3.3.15)
Формула (3.3.15) лежит в основе всех квазиньютоновских методов [1].

К началу k-й итерации известна некоторая аппроксимация B_k матрицы Гессе. Матрица B_k хранит информация о кривизне функции, накопленную на предыдущих k-1 итерациях. Используя B_k в качестве матрицы Гессе, очередное направление квазиньютоновского поиска определяется как решение аналогичной 3.3.4 системы уравнений:

(3.3.16)

Если не имеется дополнительной информации, то матрица B₀ принимается равной единичной матрице, при этом первая итерация квазиньютоновского метода будет эквивалентна шагу наискорейшего спуска.

После определения точки приближение B_k обновляется с учетом вновь полученной информации о кривизне, т.е. совершается переход от матрицы B_k к матрице B_k+1, задаваемой формулой пересчета вида

(3.3.17)

где U_k- некоторая поправочная матрица.

Обозначая , а приращение градиента через основное свойство всех квазиньютоновских правил пересчета (3.3.17) выразится равенством

(3.3.18)

В силу 3.3.15 оно означает, что B_k+1 будет правильно отражать кривизну целевой функции S (3.2.4) вдоль .

Матрица Гессе является симметричной и положительно определенной, поэтому естественно требовать, чтобы её квазиньютоновские приближения B_k обладали теми же свойствами. Пересчитывать матрицу B_k+1 из 3.3.17 можно различными способами. Вот некоторые из формул , обеспечивающих симметричность квазиньютоновских приближений [1]:

(3.3.19)

Выражение 3.3.19 называют симметричной формулой ранга один, т.е. второе слагаемое сформировано с использованием векторов первого ранга. Следующее выражение с поправками второго ранга называется формулой Дэвидона-Флетчера-Пауэлла (ДФП или DFP) и выглядит следующим образом [1]:

, (3.3.20)

где

Часто используемой является формула Бройдена - Флетчера - Гольдфарба -Шанно (БФГС или BFGS - формула):

(3.3.21 а)

Которая упрощается, если шаг s_k определялся из условия в предположении, что шаг осуществляется в направлении :

(3.3.21 б)

Для формул (3.3.21 а) условие положительной определенности выполняется если .
Теперь, учитывая особенности задачи в случае использования метода наименьших квадратов, система уравнений для расчета направления поиска выглядит так:

(3.3.22)

Условие, которому должно подчиняться очередное квазиньютоновское приближение M_k+1 запишется

, (3.3.23)

где и

Процедуру пересчета матрицы M_k можно осуществлять с использованием формул (3.3.19 – 3.3.21).