Моделирование Лузина. Виды (направления) прогнозирования
 Скачать 1.58 Mb.
|
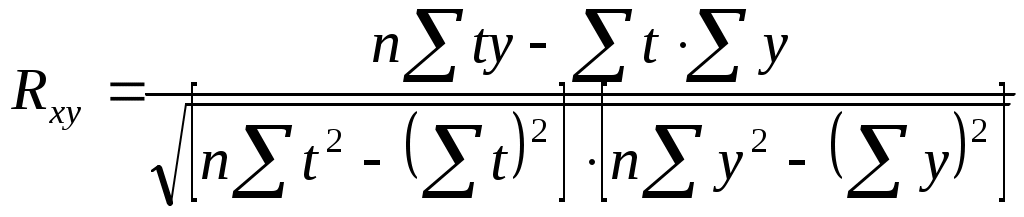  Следовательно, связь между временем и среднемесячной начисленной зарплатой работников прямая, т.к. Rxy 0, а теснота связи умеренная (по шкале Чеддока). Коэффициент детерминации равен R2xy= (0,3)2=0,09 (9%). Следовательно, 9% изменений среднемесячной начисленной зарплатой работников объясняется изменением времени. Коэффициент корреляции между временем и уровнем рентабельности деятельности сельхозпредприятий определяется по формуле (в качестве факторного признака Х выступает номер года t, а в качестве результативного признака Y выступает Х): 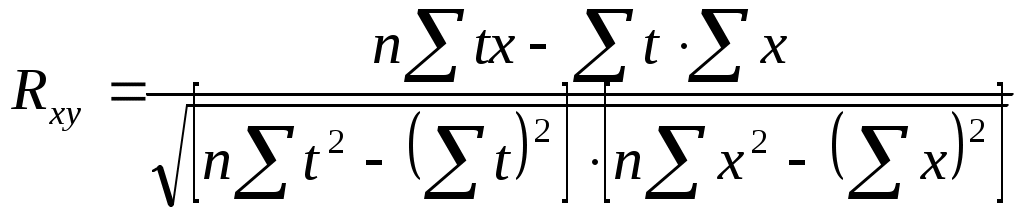  Следовательно, связь между временем и уровнем рентабельности деятельности с/х предприятий на 1 га удобренной площади прямая, т.к. Rxy 0, а теснота связи умеренная (по шкале Чеддока). Коэффициент детерминации равен R2xy= (0,49)2=0,24 (24%). Следовательно, 24% изменений уровня рентабельности деятельности с предприятий объясняется изменением времени. Коэффициент корреляции между среднемесячной начисленной зарплатой работников и уровнем рентабельности деятельности с\х предприятий определим по формуле: 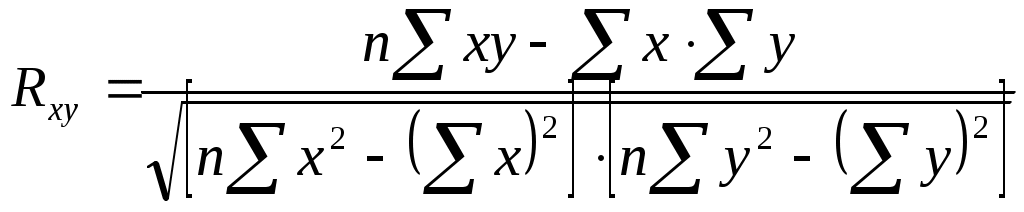  Следовательно, связь между среднемесячной начисленной зарплатой работников и уровнем рентабельности деятельности с/х предприятий прямая, т.к. Rxy 0, а теснота связи слабая (по шкале Чеддока). Коэффициент детерминации равен R2xy= (0,21)2=0,04 (4%). Следовательно, 4% изменений среднемесячной начисленной заработной платы работников объясняется уровнем рентабельности деятельности с/х предприятий. Таблица 4.3 Данные о надое молока, полученном сельскохозяйственными товаропроизводителями, и расходе кормов на 1 голову крупного рогатого скота в области за 1999-2008 гг.
По данным табл.4.3. Анализ по данным об объеме инвестиций и стоимости сельскохозяйственной продукции в области за 1999-2008 гг. Построим диаграммы, показывающие зависимость каждого из показателей от времени (x – t, y – t) и друг от друга (х – у). 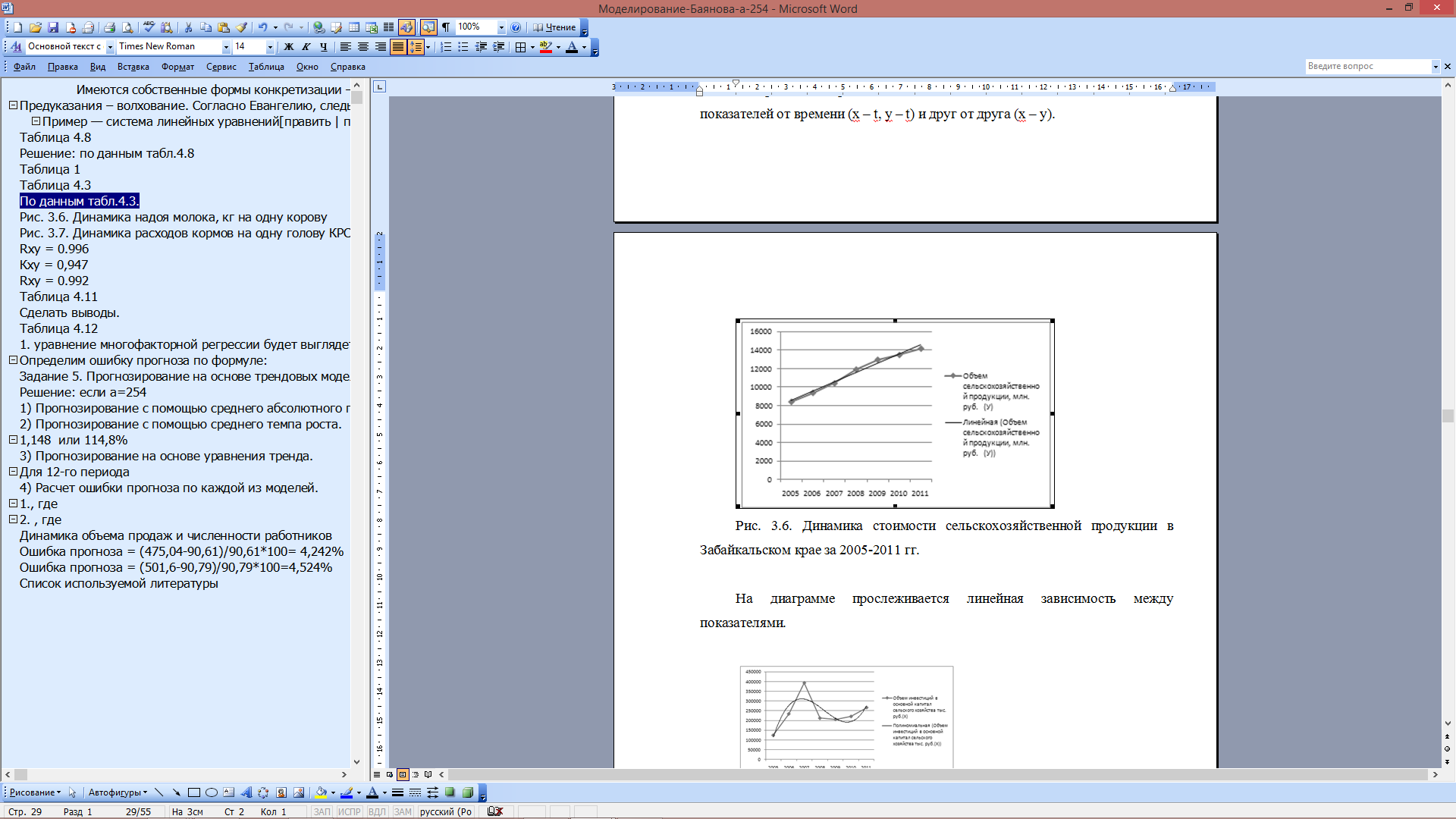 Рис. 4 Динамика стоимости сельскохозяйственной продукции в области за 1999-2008 годы На диаграмме прослеживается линейная зависимость между показателями. 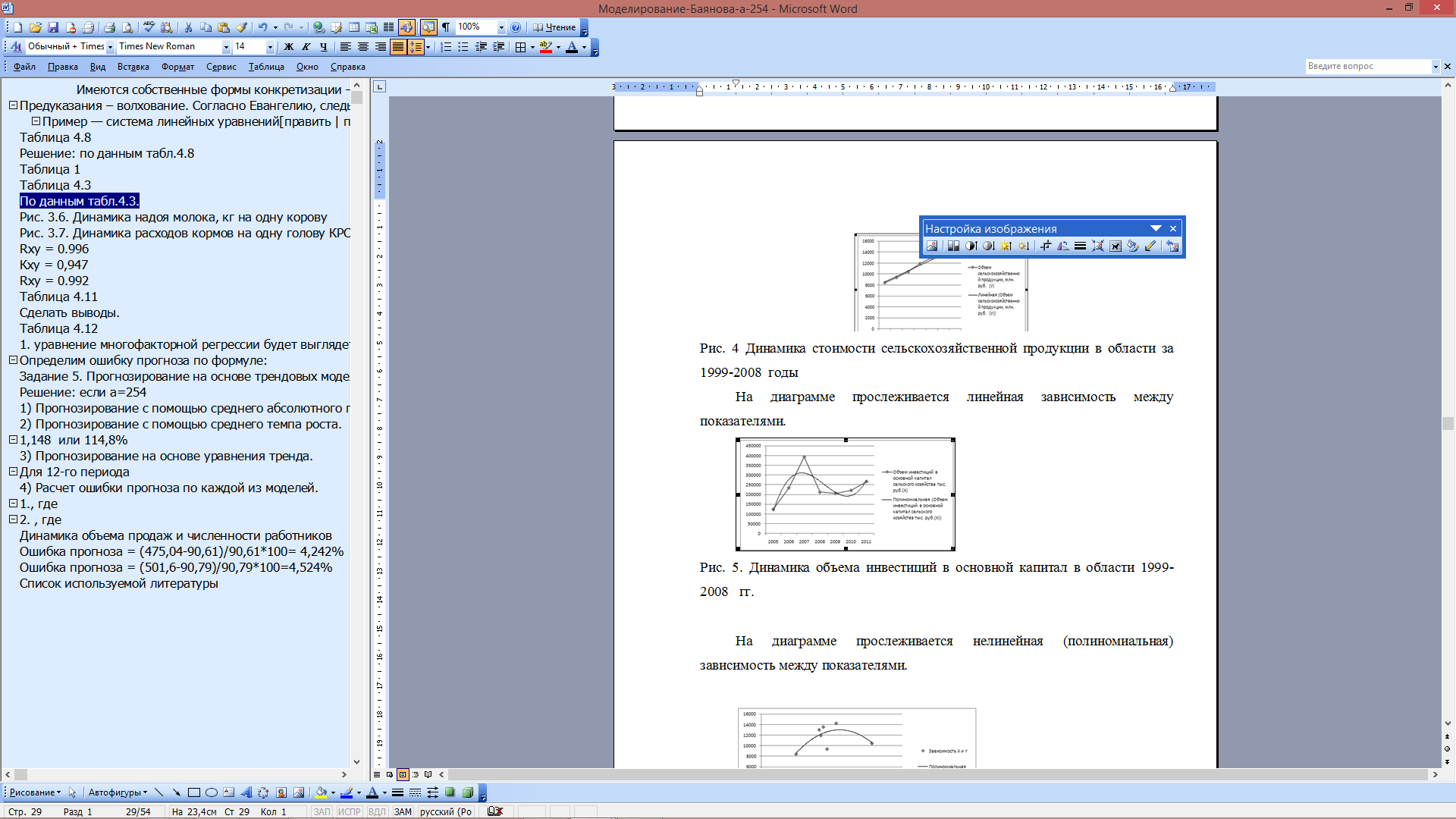 Рис. 5. Динамика объема инвестиций в основной капитал в области 1999-2008 гг. На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. 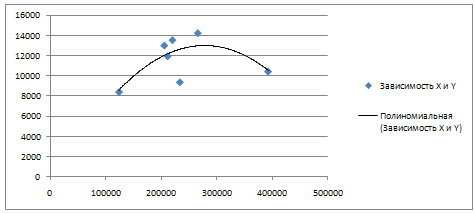 Рис. 6 Зависимость между объемом инвестиций и стоимостью сельскохозяйственной продукции в в области за 1999-2008 годы На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. Коэффициент корреляции между временем и объемом сельскохозяйственной продукции определим по формуле (в качестве факторного признака Х выступает номер года t):   0,991Следовательно, связь между временем и объемом сельскохозяйственной продукции в области, т.к. Rxy > 0, а теснота связи весьма высокая (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,991)2 = 0.982 или (98,2%). Следовательно, 98,2% изменений объема сельскохозяйственной продукции в области объясняется изменением времени. Коэффициент корреляции между временем и объемом инвестиций в основной капитал в Забайкальском крае определим по формуле (в качестве факторного признака Х выступает номер года t, а в качестве результативного признака Y выступает Х):   0.201Следовательно, связь между временем и объемом инвестиций в основной капитал в области, т.к. Rxy > 0, а теснота связи слабая (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,201)2 = 0,040 (4%). Следовательно, 4% изменений объема инвестиций в основной капитал в области объясняется изменением времени. Коэффициент корреляции между объемом инвестиций в основной капитал и объемом сельскохозяйственной продукции в области определим по формуле:   0.164Следовательно, связь между объемом инвестиций в основной капитал и объемом сельскохозяйственной продукции в области прямая, т.к. Rxy > 0, а теснота связи слабая (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,164)2 = 0,027 (2,7%). Следовательно, 2,7% изменений объема сельскохозяйственной продукции в области объясняется изменением объема инвестиций в основной капитал. Анализ по данным о надое молока, полученном сельскохозяйственными товаропроизводителями, и расходе кормов на 1 голову крупного рогатого скота в в области 1999-2008 гг. Построим диаграммы, показывающие зависимость каждого из показателей от времени (x – t, y – t) и друг от друга (х – у). 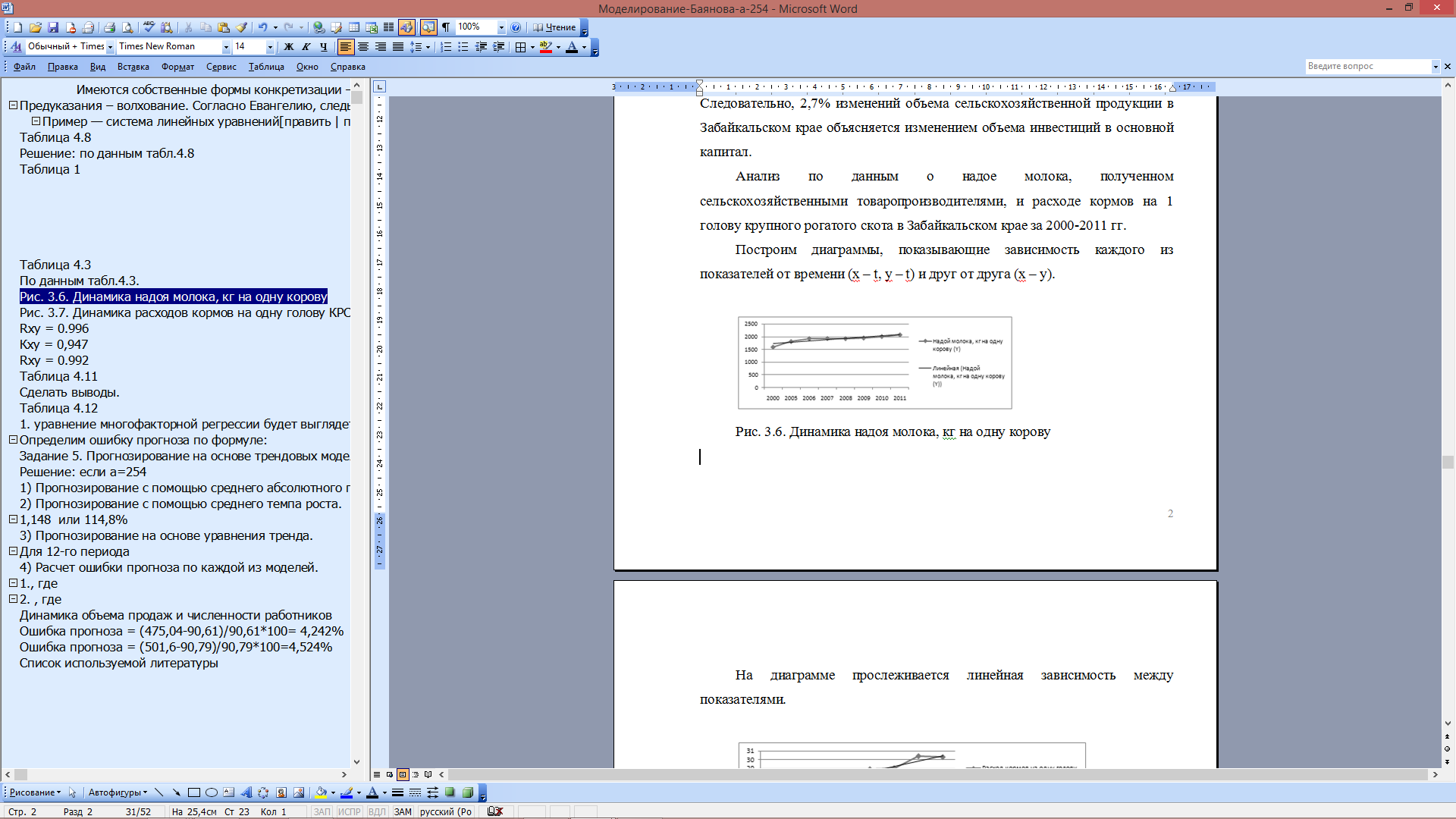 Рис.7 Динамика надоя молока, кг на одну корову На диаграмме прослеживается линейная зависимость между показателями. 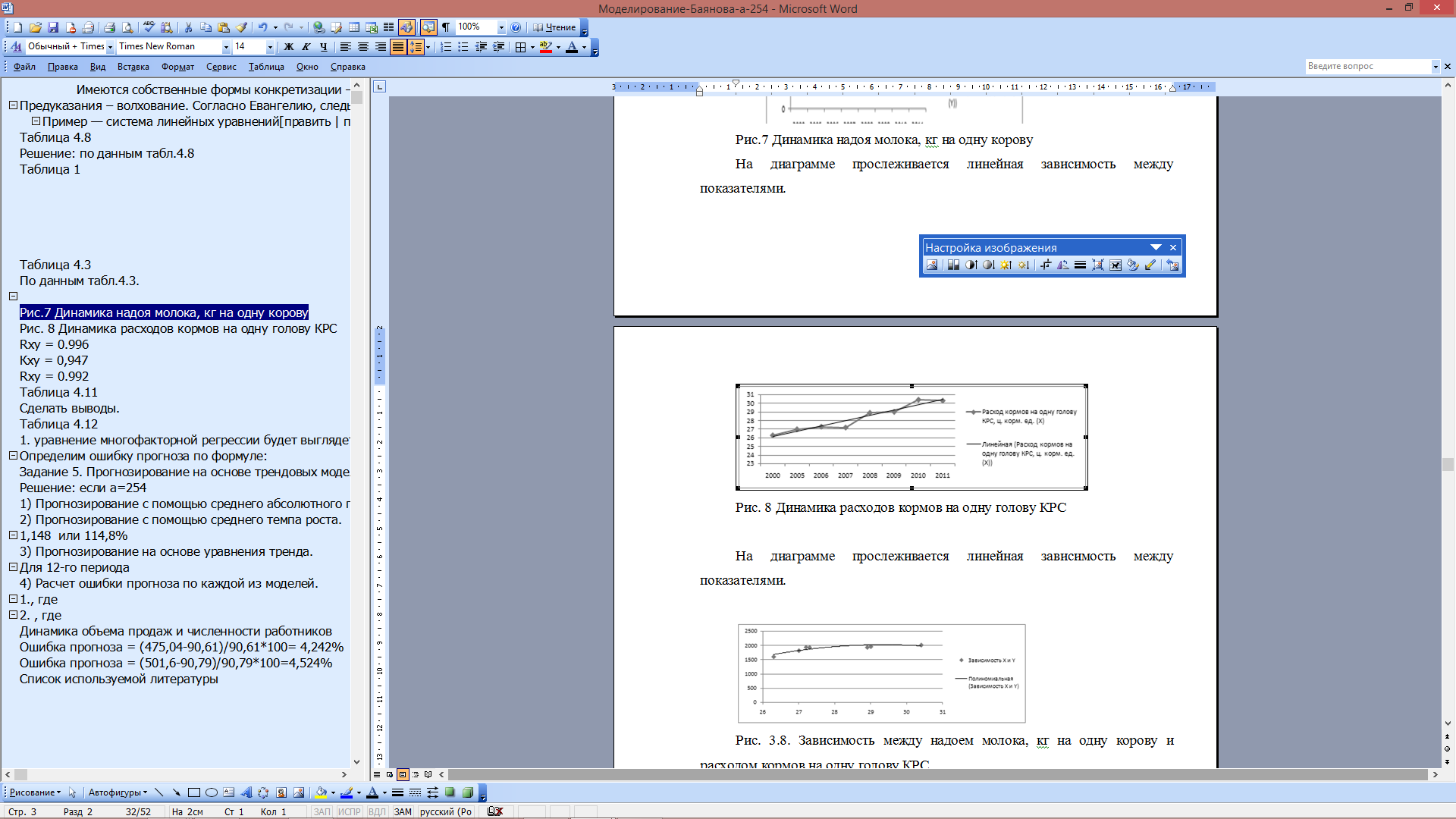 Рис. 8 Динамика расходов кормов на одну голову КРС На диаграмме прослеживается линейная зависимость между показателями. 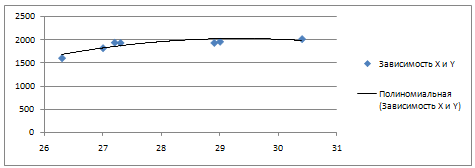 Рис. 9. Зависимость между надоем молока, кг на одну корову и расходом кормов на одну голову КРС На диаграмме прослеживается нелинейная (полиномиальная) зависимость между показателями. Коэффициент корреляции между временем и надоем молока определим по формуле (в качестве факторного признака Х выступает номер года t): Rxy = 0.996 Следовательно, связь между временем и надоем молока прямая, т.к. Rxy > 0, а теснота связи весьма высокая (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,996)2 = 0.991или (98,2%). Следовательно, 99,1% изменений надоя молока объясняется изменением времени. Коэффициент корреляции между временем и расходом кормов на одну голову КРС определим по формуле (в качестве факторного признака Х выступает номер года t, а в качестве результативного признака Y выступает Х): Кxy = 0,947 Следовательно, связь между временем и расходом кормов на одну голову КРС определим прямая, т.к. Rxy > 0, а теснота связи весьма высокая (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,947)2 = 0,896 (89,6%). Следовательно, 89,6% изменений расхода кормов на одну голову КРС объясняется изменением времени. Коэффициент корреляции между надоем молока и расходом кормов на одну голову КРС определим по формуле: Rxy = 0.992 Следовательно, связь между надоем молока и расходом кормов на одну голову КРС прямая, т.к. Rxy > 0, а теснота связи весьма высокая (по шкале Чеддока). Коэффициент детерминации равен R2xy = (0,992)2 = 0,984 (98,4%). Следовательно, 2,7% изменений объема сельскохозяйственной продукции в Забайкальском крае объясняется изменением объема инвестиций в основной капитал. Задание 3. По приведенным в табл. 4.11 данным, построить однофакторную линейную модель типа у=a+bx. Таблица 4.11
Оцените качество модели с помощью коэффициента детерминации, средней ошибки аппроксимации и F-критерия Фишера. Табличное значение F-критерия Фишера (F табл. ) равно 10,13 при Р=0,95. Выполнить прогноз на следующие три периода и рассчитать ошибку прогноза, если х изменялся следующим образом:
Сделать выводы. Решение: Если а=154. Определим фактические значения:
Для построения однофакторной линейной модели типа у=а+bx, необходимо определить ее параметры. Для этого построим вспомогательную таблицу:
С 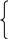 оставим и решим систему нормальных уравнений, для нахождения параметров уравнения регрессии.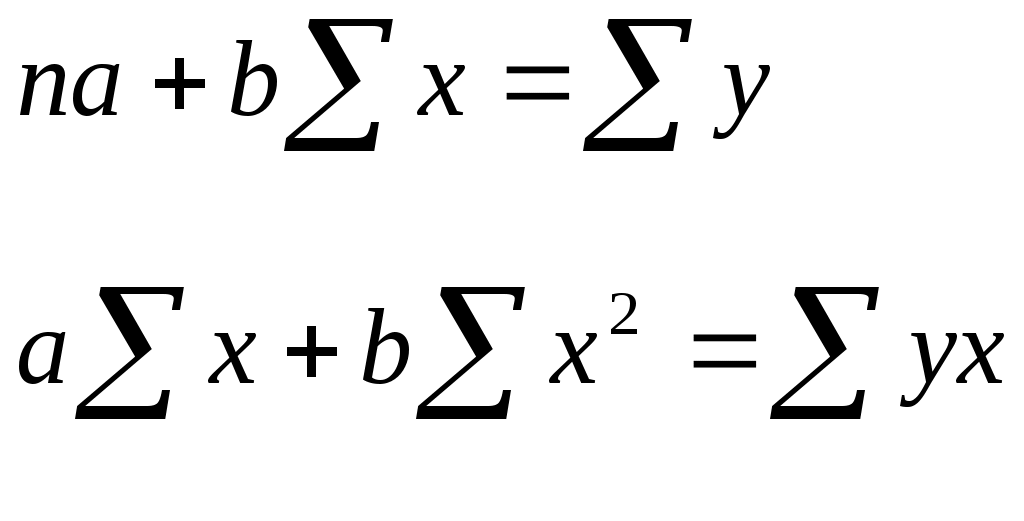 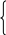  Д 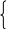 ля решения системы, умножим каждое значение первого уравнения на 2,26 и получим: Далее путем вычитания первого уравнения из второго получим: -9,71b = -12,76 b = 1,314 Подставим значение b в любое уравнение и найдем параметр a: 4а+9,04*1,314=51,72 4а=39,84 а=9,96 однофакторная линейная модель примет вид: у=9,96+1,314*х. Экономическая интерпретация, полученной модели: при увеличении фактора х на 1 единицу своего измерения результативный признак Y увеличивается на 1,314 единиц своего измерения. Качество регрессионной модели считается высоким, если: - коэффициент детерминации больше или равен 0,5%; - средняя ошибка аппроксимации менее или равна 10%; - Fтабл Fфакт. Найдем перечисленные показатели. Для нахождения коэффициента детерминации необходимо знать коэффициент корреляции, который определим по формуле: 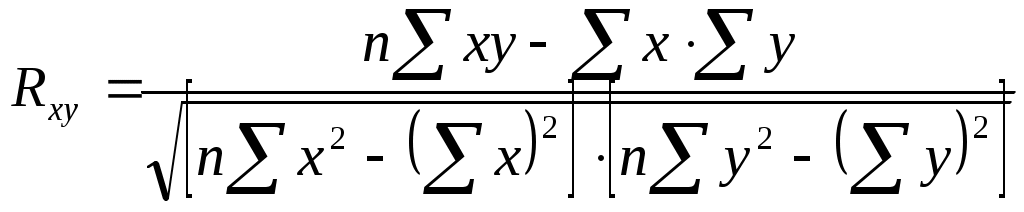 Следовательно, связь между Y и Х прямая, т.к. Rxy0, а теснота связи весьма высока (по шкале Чеддока). Коэффициент детерминации равен R2xy= (0,97)2=0,94 (94%). Следовательно, 94% изменений результативного признака Y объясняется изменением фактора Х. В нашем случае коэффициент детерминации больше 0,5, следовательно, первое условие, определяющее высокое качество модели выполнилось. Для расчета средней ошибки аппроксимации построим вспомогательную таблицу:
Определим среднюю ошибку аппроксимации по формуле: |