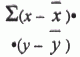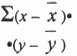Моделирование Лузина. Виды (направления) прогнозирования

• Название: Виды (направления) прогнозирования
• Дата: 18.04.2022
• Размер: 1.58 Mb.
• Имя файла: Моделирование Лузина.doc
• Тип: Документы; #482592
• страница: 1 из 6

3. История развития прогнозирования
Данные археологии и этнографии показывают, что первобытное мышление после долгого развития выработало представление о прошлом и гораздо позднее о будущем как о чем-то отличном от настоящего. Даже позднее представление о цепи событий как о причинно-следственном логическом процессе было довольно смутным. По сути, время существовало только одно – настоящее. Затем к нему добавилось другое – «иное, нереальное, мифическое», где действовали герои мифов и сверхъестественные силы. Затем совершился переход к конструированию «иного мира в ином времени» – «иное будущее».

Предвидением будущего занимались, занимаются и будут заниматься во все времена. Хотя церковь, как правило, негативно относится к людям, занимающимся прогнозированием. Например, Библия говорит, что будущее человеку вообще нельзя знать. Сократ же приветствовал прогнозирование (мантику): “Мантика – орудие человеческого успеха, а это оправдывает ее существование”.

Официально прогнозирование (футурология) родилось в России в 1943 году.

Виды (направления) прогнозирования. Условно в прогнозировании можно выделить 4 направления: эзотерическое; религиозное; астрологическое; научное. В научном прогнозировании зарождается новое направление – комплексное,которое порой учитывает все направления.

Каждый из видов прогнозирования имеет свои «подвиды». Например, бесчисленные откровения, произведения по религиозной эсхатологии, философия истории и социальные утопии, которые продолжают существовать и в наше время.

Эзотерическое прогнозирование основано на предвосхищении и имеет три вида откровений:

1.   механический –одержимость, “физические манифестации”;

2.   эмоциональный –произнесение и написание слов в состоянии транса;

3.   духовный – экстаз, озарение (подобное происходит со святыми и пророками).

Имеются собственные формы конкретизации – предсказания и предуказания:

предсказания:откровения, предвидение, прорицания, гадания;

предуказания: предопределения, волхования, заклинания, просьбы-мольбы и пр.

Предсказания – предвидениево многом зависит от интуиции и не имеет никакого отношения к науке. У древних народов искусство предсказания получила название “мантика”, и оно было самостоятельным направлением деятельности магов и гадателей. Самыми первыми предсказателями можно считать древних пророков, которые чудесным образом видели будущее. Об этом, например, говорится в Ветхом Завете.

Самыми уважаемыми пророками в древности считались жрецы Древней Греции, ценившие больше всего в жизни гармонию. Наиболее знаменитыми оракулами у них считались Дельфийские, которые первоначально назывались Пифонами.

В особом ряду пророков стоят святые отцы, праведники.

Предсказания носили иногда странный характер: в виде вещих снов (примеры находим в Библии); видений (например, видений Сергия Радонежского Богоматери); слышание голоса неизвестного предсказателя – “вмешательство гения” (как было у Сократа); с помощью “потока сил из вечности” (как предсказывал Нострадамус); автоматического письма (как это было у предсказательницы Сибиллы, которая предсказывала на многие столетия вперед судьбы героев, наций и государств).
Предуказания–волхование.Согласно Евангелию, следы трех волхвов, 2000 лет тому назад предсказавших рождение Иисуса Христа, ведут на Восток. Волхвы были у египтян, которые использовали тайные знания для усиления власти жреческого сословия. В истории мидян и персов есть свидетельство тому, что некая одна каста (племя) обладала тайными магическими знаниями. Ассиро-Вавилонские волхвы существовали независимо от жрецов и занимались толкованиями снов, предсказаниями, астрономией и астрологией. У них был свой Учитель (“раб-маг”), который наряду с другими высшими чиновниками (“раб-сарис” и “раб-сак”) являлся советником вавилонского царя. Иногда волхвы делились по четырем кланам: “хертуммимы” (составляли заговоры, снимали сглаз); “ашшафимы” (составляли одни заклинания); “мекашафимы (составляли другие заклинания); “газеримы” (астрологи, наблюдавшие астрономические явления и по ним занимающиеся предсказаниями). Однако, независимо от этого деления все они обладали тайными знаниями, и всех их называли халдеями. От ассиро-вавилонян волхование перешло к персам, где волхвам пришлось бороться с сильной жреческой кастой, не желавших терять единовластие. Но затем произошло объединение волхвов и жрецов, и слово маг у персов стало синонимом слова жрец. Греки в Азии в свою очередь восприняли волхование от персов и перенесли его в Европу. Затем волхование переняли римляне. Так к магии приобщились многие народы. Но волхвов чаще воспринимали как чародеев, колдунов и заклинателей. В Древнем Египте информацией владели ученые-жрецы. Волхование считалось даром богов – высшим проявлением таланта и избранности. Фараоны, цари и императоры были к волхвам благосклонны и особо их почитали. К ритуалу предсказаний жрецы Древней Греции готовились заранее – за 3 дня. Они очищались, голодали и купались в святом колодце. Служили оракулу пифии – это были молодые девушки (только девственницы), избранные из наиболее нервных и впечатлительных. Пифии под действием наркотических трав впадали в транс и “вещали”.
Представителями эзотерического прогнозирования 18-20 века были, например, русский генералБрюсс (ученый,друг и соратник русского царя Петра Первого), сын еврейского народа Вольф Мессинг (родился в1899 г.), болгарка Ванга (Вангелия Пандева) (1912-1996 гг.).

Форм хранения предсказаний. В античном мире, а затем и в другие времена в разных странах существовало множество форм хранения предсказаний: записи, предания и мифы. К древним методам прогнозирования относились, например, “Книга Перемен” (“Ицзин” или “Чинг”, 2852-2737 года до н.э.), в ней 64 пророчества записаны гексаграмами по принципу двоичного кода (“да-нет”); древнеегипетское карточное “Предсказательное Таро” (“Книга Тота”); нумерология Пифагора (5-6 век до н.э.). Вековые тайны скрываются в древневосточном эпосе, книгах библейских пророков, например, “Апокалипсис” Иоанна Богослова (написанный в 67-68 годах), халдейских мудрецов. Присутствуют они и в мировых шедеврах. Это “Илиада” и “Одиссея” (Гомер), “Энеида” (Вергилий), “Повесть временных лет” (Нестор), “Новая жизнь” и “Божественная комедия” (Данте), “Фауст” (Гете).

Религиозные концепции будущего обычно использует духовный вид откровений, и они формировались по трем направлениям на основе:

1.   первобытной  мифологии;

2.   мировой индуистско-буддистско-джайнистской религии;

3.   мировой иудаистско-христианско-мусульманской религии.

Первобытная мифология основывалась на примитивных мифах и сказок о явлениях природы, об обычаях и родовых нравах, судьбах умерших, о «конце света».

Индуистско-буддистско-джайнистская концепцияпредставляет историю в виде постоянной смены циклов регресса (охватывающих миллионы лет), от «золотого века» к «концу света», затем «сотворение нового мира», вновь регресса и т.д. без конца. Счастливое будущее с таких позиций видится в том, чтобы «добродетельным поведением» избавиться от бесконечных «перевоплощений» души после смерти, от этого вечного «коловращения» мироздания и попасть в «нирвану» – качественно иное состояние, при котором отсутствуют и желания и страдания. Такие взгляды характерны для современной религиозной идеологии в обширном регионе Юго-Восточной Азии, и с ними приходится сталкиваться на международных конференциях или в литературе.

Иудаистско-христианско-мусульманская концепция- согласно ей «история будущего» представляется в виде прихода «спасителя-мессии», установления «царства божия», наступления «конца света», «страшного суда». И, наконец, переход в качественно новое состояние «вечного блаженства» для праведников и «вечных мук» для грешников.

Самыми первыми предсказателями этого направления можно считать древних пророков, которые чудесным образом видели будущее. Среди них, например: Монах Авель (1757-1841),Игумен Серафим (Кузнецов) (1920), Преподобный Феофилакт-исповедник, епископ Никомидийский (9 век), Отец Варсонофий (Плиханков) (1845-1913), Преподобные Варсануфий и Иоанн (6 век), Блаженная Матрона (19-20 век), Св. прав. Иоанн Кронштадтский (19-20 век).

Религиозные направления и сейчас популяризируются в литературе и на разных конференциях, они оказали сильнейшее влияние на эволюцию утопизма и идеалистической философииистории и сформировали целый ряд учений и идей:

«воздаяние» в загробном мире сообразно поведению человека при жизни;

провиденциализм – божественное провидение, якобы целенаправленно определяющее ход событий независимо от воли человека;

мессианизм – упование на приход «спасителя-мессии», который радикально изменит к лучшему существующие порядки и т.д.

  В древние века предсказание жрецами солнечных и лунных затмений, появления комет считалось чудом.

Астрология – астрономические расчеты с элементами личного восприятия. Астрологи(“математики” или “маги”; в наше время их называют космобиологами) по положению созвездий, планет, Луны и астероидов относительно Земли составляли “карту” человека, страны или события на момент их появления или рождения и трактовали ее согласно своим знаниям, таланту, воображению и уровню развития. Поэтому можно сказать, что астрология находится в промежутке между эзотерикой и астрономией. Среди российских астрологов, например, можно выделить: друга русского царя Петра Первого генерала Брюсса; наших современников А.Зараева, А.Каменского, П.Глоба.

Космобиология (солнечно-земные связи).В наше время к научному направлению этого вида прогнозов относятся солнечно-земные связи. Направление начало зарождаться более 2 тысяч лет тому назад, но облекло научную форму с начала 20 века благодаря астрономическим наблюдениям за Солнцем – солнечной активности (СА). Прородителем этого направления является русский ученый-космист А.Чижевский.

Солнечная активность (СА) – это совокупность нестационарных явлений на Солнце, возникающих и развивающихся в отдельных активных областях, а также совокупность таких активных областей (АО). Здесь образуются группы пятен, флоккулы, протуберанцы, волокна, корональные детали, магнитные поля.

Природа любых земных событий, а также механизм ее рассматривается современной наукой в двух гипотезах:

эндогенной (внутренней), где причины следует искать прежде всего в самой Земле и тех процессах, которые протекают на ней и в ее недрах,

экзогенной (внешней), которая считается, что причины находятся за пределами Земли – в Солнечной системе и Галактике.

Во внешнем воздействии выделяют следующие основные факторы:

1)   воздействие Солнца (солнечно-земные связи, А.Л. Чижевский). Влияние в этом случае идет по цепочке: солнечная активность – атмосферные процессы – геологические и другие события. Доказано, что солнечные изменения прямо пропорциональны земным;

2)   воздействие Луны (лунно-земные связи). В первую очередь приливный эффект. Лунно-земные связи были известны еще в древности;

3)   галактическое воздействие: движение Солнца вокруг ядра Галактики, пролеты звезд,

4)   теория катастроф: столкновение Земли с астероидами, метеорами и кометами. Теория катастроф возродилась в 70-е годы 20-го века, и ее прогнозами начали серьезно заниматься ученые многих стран мира.

  В научном прогнозировании можно выделить 3 основных направления:

1.     научная фантастика;

2.     размышления о будущем;

3.     технологическое прогнозирование.

Научная фантастика и размышления о будущем стали бурно развиваться в 20 веке. Среди прогнозистов этого направления (научная фантастика) Жюль Верн, Герберт Уэллс («Предвидения о воздействии прогресса механики и науки на человеческую жизнь и мысль», 1901). Размышлениями о будущем  занимались П.Гартинг, Ш.Рише, Г.Тард, Д.Менделеев, И.Мечников. Фтурологом можно считать и Ньютона, который попытался на данных Библии рассчитать будущий «Конец Света». Он говорил, что “от искусства человека зависит предугадывание божественного промысла”. К ранним футурологам первого поколения относятся также нобелевский лауреат Дж.Томсон («Предвидение будущего», 1955), К.Э.Циолковский («Будущее Земли и человечества», 1928).

Технологическое прогнозирование (концепции, течении и проблемы) – определяется, как вероятностная оценка будущего перемещения технологии, означающей весь диапазон процессов любого перемещения (вертикального и горизонтального).

Современныйнаучныйподходвозник в начале 20-го века. Среди прогнозистов этого направленияП.Сорокин (социологическое прогнозирование,1918), А.Чижевский (солнечно-земные связи, 1918), Н.Кондратьев (экономические циклы, 1927), В.А.Базаров-Руднев (технологическое прогнозирование, 1924-1927), Е.Слуцкий (1927). А также Н.Четвериков, А.Вайнштейн, Т.Райков, А.Богданов, Н.Бердяев, Л.Гумилев, В.Леонтьев и многие ученые-космисты.

Первая книга по футурологии в России была написана в 1918 году в Санкт-Петербурге Питиримом Сорокиным (в ней автор, например, предсказывал к концу 20-го века рост жестокости, бесчеловечности и распад культуры). В 1924-1928 гг. вышли в свет серии статей Б.Руднева (переизданные в 1989 году) «Каким быть плану: дискуссии 20-х годов».

В качестве признанной самостоятельной отрасли управления технологическое прогнозирование внедрилось примерно в середине 20-го века и стало применяться в широком и всевозрастающем масштабе в промышленности, научно-исследовательских институтах и военных ведомствах. Началась разработка новой технологии прогнозирования. Прогноз стал отраслью индустрии. Начался бум прогнозов, появляются работы: «Экономические прогнозы и принятие решений» и «Прикладное экономическое прогнозирование» (Г.Тейл, 1958-1965), «12 способов предсказаний» (Д.Белл, 1964), «Социальная технология» (О.Гелмер, 1966), «Прогнозирование научно-технического прогресса» (Э.Янч, 1967), «Прогностика» (Ф.Полак, 1968).

Экологическая проблема в 70-е годы 20 века подорвала престиж мажорных прогнозов в развитии экономики (Р.Фолк «Наша планета в опасности, 1971»). Виновником загрязнения природной среды признали современные тенденции развития научно-технического прогресса (М.Ситрон, Б.Барток «Переоценка технологии в динамической среде», 1974).

Социальное прогнозированиев своем развитии имело несколько этапов:

• 
  религиозной эсхалогии (учения о конце света), которое берет свое начало несколько тысячелетий назад и представлено пророческой деятельностью древних жрецов, волхвов, оракулов, астрологов;
  
• 
  ранней футурологии (вторая половина 19 века) – художественные «размышления о будущем», (труды Г.Уэлса, К.Э.Циолковского и др.);
  
• 
  технологического прогнозирования (вторая четверть 20-го века) (труды В.А.Базарова, Д.Бернала, Н.Винера, Р.Юнгка и др.);
  
• 
  социального прогнозирования (1970-1975г.г.) (книга А.Тоффлера «Футурошок», И.В.Бестужев-Лада «Социальное прогнозирование»).
  

9. Показатели количественного измерения тесноты связи
При изучении корреляционной связи важно выяснить не только форму, но и тесноту (сопряженность) связи между факторным и результативным признаками. Для этого статистикой установлен объективный числовой показатель, который вычисляется по определенным правилам. Чтобы измерить тесноту прямолинейной связи между двумя признаками, пользуются парным коэффициентом корреляции, который обозначается r_ху.

Так как при корреляционной связи имеют дело не с приращением функции в связи с изменением аргумента, а с сопряженной вариацией результативных и факторных признаков, то определение тесноты связи, по существу, сводится к изучению этой сопряженности, т.е. того, в какой мере отклонение от среднего уровня одного признака сопряжено с отклонением другого. Это значит, что при наличии полной прямой связи все значения   должны иметь одинаковые знаки, при полной обратной – разные, при частичной связи знаки в преобладающем числе случаев будут совпадать, а при отсутствии связи – совпадать примерно в равном числе случаев.

Покажем это на примере связи двух признаков х и у, приведенных выше. Исчислим которая также меняется в зависимости от тесноты связи, для чего предварительно установим, что:

Полная прямая связь

х	3	5	7	10
y	15	17	20	22
	-3,25	-1,25	+0,75	+3,75
	-3,5	-1,5	+1,5	+3,5
	+11,375	+1,875	+1,125	+13,125 = +27,5

Полное совпадение знаков свидетельствует о наличии полной прямой связи и при этих условиях в нашем примере

Полная обратная связь

х	3	5	7	10
у	22	20	17	15
	-3,25	-1,25	+0,75	+3,75
	+3,5	+1,5	-1,5	-3,5
	-11,375	-1,875	-1,125	-13,125 = -27,5

Полное несовпадение знаков   свидетельствует о наличии полной обратной связи и при этих условиях:

Частичная прямая связь

х	3	5	7	10
у	15	20	17	22
	-3,25	-1,25	+0,75	+3,75
	+3,5	+1,5	-1,5	+3,5
	+11,375	-1,875	-1,125	+13,125 = +21,5

Частичное совпадение знаков   свидетельствует о преобладании прямой связи, и при этих условиях



Частичная обратная связь

х	3	5	7	10
у	22	17	20	15
	-3,25	-1,25	+0,75	+3,75
	+3,5	-1,5	+1,5	-3,5
	-11,375	+1,875	+1,125	-13,125 = -21,5

 

Частичное совпадение знаков   указывает о преобладании обратной связи, и при этих условиях



Полное отсутствие связи

х	3	5	7	10
у	20	15	22	17
	-3,25	-1,25	+0,75	+3,75
у =	+5	-3,5	+3,5	-1,5
Σ(υ-х)(у-у)	-4,875	+4,375	+2,625	-5,625 = -3,5

Частичное совпадение знаков   при условии, что   близка к нулю, свидетельствует об отсутствии связи между признаками.

Таким образом, по показателю 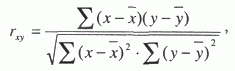  можно определить направление и тесноту связи, но он неудобен, так как зависит от числа членов ряда и единиц измерения. Математически доказано, что   достигает максимума при полной прямой связи и минимума при полной обратной связи. Следовательно, если бы во всех случаях можно было знать максимум   то отношение фактического выражения к своему максимуму позволило бы определить степень связи, т.е. в какой мере фактическая связь близка или далека от полной связи. Математически доказано, что максимум выражения

 поэтому теснота связи определяется как отношение



где r_ху – линейный коэффициент корреляции.

Коэффициент корреляции принимает значение от -1 до +1, причем если r_ху>0, то корреляция прямая, если r_ху<0, то корреляция обратная, а если r_ху = 0, то связь отсутствует полностью.

В зависимости от того, насколько r_ху, приближается k±1, различают связь слабую, умеренную, заметную, высокую, тесную и весьма тесную.

Коэффициент корреляции может быть исчислен и по следующей формуле, которая тождественна приведенной выше, но удобнее для расчетов (особенно на компьютерах и другой вычислительной технике).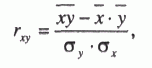

 

где σ_у– среднее квадратическое отклонение результативного признака;

σ_х– среднее квадратическое отклонение факторного признака.

Зная коэффициент корреляции, можно определить и параметры уравнения регрессии, потому что 

Коэффициент корреляции r_ху, применяется только в тех случаях, когда между явлениями существует прямолинейная связь. Если же связь криволинейная, то пользуются индексом корреляции, который исчисляется по формуле: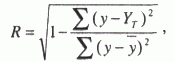



где у – первоначальные значения;  – среднее значение; Y_T– теоретические (выровненные) значения переменной величины.

 Показатель 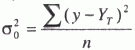  – остаточная, случайная дисперсия. Она характеризует размер отклонений эмпирических значений результативного признака у от теоретических Y_T, т.е. случайную вариацию.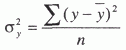

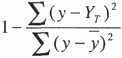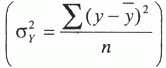 – общая дисперсия. Она охарактеризует размер отклонений эмпирических значений результативного признака у от   т.е. общую вариацию. Отношение случайной дисперсии к общей характеризует долю случайной вариации в общей вариации, а   есть не что иное, как доля факторной вариации   в общей, потому что по правилу сложения дисперсий общая дисперсия равна сумме факторной и случайной дисперсии: σ² = σ²у + σ²₀

Подставим в формулу индекса корреляции соответствующие обозначения случайной, общей и факторной дисперсий и получим: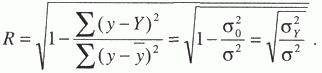



Таким образом, индекс корреляции характеризует долю факторной корреляции в общей 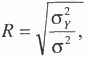  однако с той только разницей, что вместо групповых средних берутся теоретические значения Y.

Индекс корреляции по своему абсолютному значению колеблется в пределах от 0 до 1. При функциональной зависимости случайная вариация Σ (у – Y)² =0, индекс корреляции равен 1. При отсутствии связи R = 0, потому что 

 Коэффициент корреляции является мерой тесноты связи только для линейной формы связи, а индекс корреляции и для линейной, и для криволинейной.При прямолинейной связи коэффициент корреляции по своей абсолютной величине равен индексу корреляции ІrІ = R.

Если индекс корреляции возвести в квадрат, то получим коэффициент детерминации, 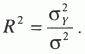Он характеризует роль факторной вариации в общей вариации и по построению аналогичен корреляционному отношению В нашем примере коэффициент детерминации R² = 0,567. Это значит, что 56,7% всей вариации обусловлено изучаемым фактором, т.е. возрастом рабочего. Как и корреляционное отношение, коэффициент детерминации R²может быть исчислен при помощи дисперсионного анализа, так как дисперсионный анализ позволяет расчленить общую дисперсию на факторную и случайную. Однако при дисперсионном анализе для разложения дисперсии пользуются методом группировок, а при корреляционном анализе – корреляционными уравнениями.

Коэффициент детерминации является наиболее конкретным показателем, так как он отвечает на вопрос о том, какая доля в общем результате зависит от фактора, положенного в основание группировки.

При прямолинейной парной связи факторную дисперсию можно определить без вычисления теоретических значений Y по следующей формуле:



Оценка существенности связи в корреляционном анализе проводится так же, как и в дисперсионном: определяется число степеней свободы К₁ = т – 1 и К₂= n – т, только т – не число групп, а число параметров в уравнении регрессии. Если уравнение линейное, то т = 2 (параметры а₀и а₁), если криволинейное, выраженного параболой второго порядка, то т = 3 (параметры а₀, а₁и а₂) и т.д. Критические значения коэффициента детерминации R²определяются по тем же таблицам, что и для корреляционного отношения µ². Чтобы оценить существенность связи при помощи критерия Фишера, пользуются формулой: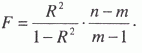



17. Метод наименьших квадратов
Метод наименьших квадратов (МНК, англ. OrdinaryLeastSquares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

До начала XIX в. учёные не имели определённых правил для решения системы уравнений, в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (1795) принадлежит первое применение метода, а Лежандр (1805) независимо открыл и опубликовал его под современным названием (фр. Méthode des moindres quarrés). Лаплас связал метод с теорией вероятностей, а американский математик Эдрейн (1808) рассмотрел его теоретико-вероятностные приложения. Метод распространён и усовершенствован дальнейшими изысканиями Энке,Бесселя, Ганзена и других.

Работы А. А. Маркова в начале XX века позволили включить метод наименьших квадратов в теорию оценивания математической статистики, в которой он является важной и естественной частью. Усилиями Ю. Неймана, Ф.Дэвида, А. Эйткена, С. Рао было получено немало важных результатов в этой области.

Пусть   — набор   неизвестных переменных (параметров),  ,  ,   — совокупность функций от этого набора переменных. Задача заключается в подборе таких значений x, чтобы значения этих функций были максимально близки к некоторым значениям  . По существу речь идет о «решении» переопределенной системы уравнений  ,   в указанном смысле максимальной близости левой и правой частей системы. Сущность МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей   . Таким образом, сущность МНК может быть выражена следующим образом:

.

В случае, если система уравнений имеет решение, то минимум суммы квадратов будет равен нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть, говоря нестрого, количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор   в смысле максимальной близости векторов   и   или максимальной близости вектора отклонений  к нулю (близость понимается в смысле евклидова расстояния).