Моделирование Лузина. Виды (направления) прогнозирования
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
|
В среднем расчетные значения отклоняются от фактических на 4,08%. Ошибка аппроксимации небольшая (А8%), регрессионная модель хорошо описывает изучаемую закономерность. Второе условие, определяющее высокое качество модели выполнилось. Определим фактическое значение критерия Фишера по формуле: 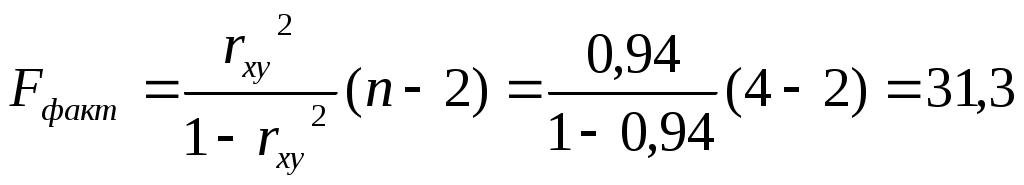 По условию задачи Fтабл Fфакт. Если Fтабл Fфакт, то гипотеза Н0 – о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность с вероятностью 1-а, следовательно, принимается гипотеза Н1. Третье условие, определяющее высокое качество модели выполнилось. Так как все условия, определяющие высокое качество модели выполняются, то модель у=9,96+1,314*х вида может быть использована для прогнозирования признака Y от фактора Х. Прогнозирование по линейной однофакторной регрессии осуществляется путем подстановки ожидаемого значения х в уравнение регрессии. Определим ожидаемые значения х в прогнозных периодах:
Выполним прогноз на следующие 3 периода: у5 = 9,96+1,314*4,767 = 16,22 у6 = 9,96+1,314*5,105 = 16,67 у7 = 9,96+1,314*5,192 = 16,78 Рассчитаем ошибки прогноза по формуле: Вывод: однофакторная линейная модель примет вид у=9,96+1,314*х. Следовательно, при увеличении фактора х на 1 единицу своего измерения результативный признак Y увеличится нам 1,314 единиц своего измерения. Данная модель может быть использована для прогнозирования признака Y от фактора Х, т.к. выполняются все условия, определяющие ее высокое качество. Наиболее точным оказался прогноз на 5-ый период (соответствует минимальное значение ошибки прогноза). Задание 4. Прогнозирование по многофакторным регрессионным моделям По приведенным в табл. 4.12 данным построить уравнение многофакторной линейной регрессии, если а = а/11,5 ,b1=(a/8)-10, b2=(1/a)+0,79, b3=0,1-(1/a), b4=(1/a)+0,5, b5=(1/a)+0,4. Таблица 4.12 Фактические значения х
Рассчитать значения результативного показателя на следующие 2 периода. На основе матрицы парных коэффициентов корреляции (табл.4.13) (рассчитать) выявить и устранить мультиколлинеарные факторы. После их устранения построить уравнение регрессии по новым данным регрессионного анализа, характеризующее зависимость результирующего показателя (y) от факторных (x i ) в линейной форме. Таблица 4.13
Рассчитать прогнозные значения результативного показателя по скорректированной многофакторной модели на следующие 2 периода, если:
Оценить точность прогноза, рассчитав ошибку прогноза для обоих случаев. Сделать выводы. Решение: Если а=154. 1. уравнение многофакторной регрессии будет выглядеть следующим образом: y = 22,09 + 21,75x1 + 0,79x2 + 0,1x3 + 0,5x4 + 0,4x5 Рассчитаем прогнозные значения Y:
Определим ошибку прогноза по формуле: Проверим модель на мультиколлинеарность и при необходимости устраним ее.
Найдем пары мультиколлинеарных факторов, которые удовлетворяют условию Из каждой пары необходимо исключить фактор, имеющий наименьшее значение rxiy. Рассмотрим первую пару rx1y = 0,59 rх2y=0,76 rx1y rx2y, следовательно, факторный признак х1 следует исключить из модели, т.к. он имеет наименьшее значение rxiy в рассматриваемой паре. Рассмотрим вторую пару rx2y = 0,76 rх4y=0,297 rx2y rx4y, следовательно, факторный признак х4 следует исключить из модели, т.к. он имеет наименьшее значение rxiy в рассматриваемой паре. Итак, из модели исключаем x1 и x4, модель примет вид: y = 22,09 + 0,79x2 + 0,1x3 + 0,4x5 Рассчитаем скорректированный прогнозные значения Y:
Определим ошибку прогноза по формуле: Вывод: более качественной является трехфакторная регрессионная модель, так как позволяет получить меньшие значения ошибки прогноза. Задание 5. Прогнозирование на основе трендовых моделей Имеются некоторые данные об объеме продаж (д.е.) за 10 лет.
Выполнить прогноз с помощью среднего абсолютного прироста, среднего темпа роста и уравнения тренда на 11-12-ый периоды. Если в 11-м периоде у будет равен (325,7 + а/100) д.е., а в 12-м периоде – (333 + а/100) д.е., рассчитать ошибку прогноза по каждой из моделей. Оцените точность прогноза по каждому периоду. Решение: если а=154 Расчет уравнения тренда ряда динамики объема продаж
1) Прогнозирование с помощью среднего абсолютного прироста. Среднегодовой абсолютный прирост объема продаж равен: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
