Инвестиционный менеджмент. инвестиционный менеджмент. Вопрос Инвестиционный менеджмент сущность и функции

• Название: Вопрос Инвестиционный менеджмент сущность и функции
• Анкор: Инвестиционный менеджмент
• Дата: 11.05.2022
• Размер: 1.4 Mb.
• Имя файла: инвестиционный менеджмент.docx
• Тип: Документы; #522440
• страница: 6 из 9

Построение регрессионной модели. Предположим, что портфель формируется из рассмотренных ранее акций фирм «А», «В» и «С». Пусть задана длительность будущего холдингового периода (для последующего сравнения модели Шарпа с моделью Марковица будем полагать, что эта длительность совпадает с выбираемой длительностью в модели Марковица) и заданы N = 10 шагов расчета в прошлом. На основании данных об изменениях рыночного индекса вычислим доходность   рыночного портфеля за N шагов расчета. Полученные данные внесем в табл. 7, где также приведены доходности   акции С, вычисленные ранее:

 

Таблица 7.

 

Условные доходности рыночного портфеля и акции С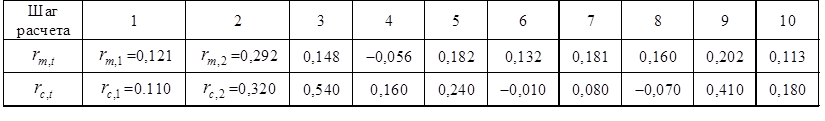

 



 

В таком случае для акции С уравнение линейной регрессии должно принимать вид:

 

= 

 

Ниже будут вычислены параметры линейной регрессии для акции С:  =0,1165 и  =0,5255. Значит, для этой акции уравнение линейной регрессии должно иметь вид:

 

 = 0,1165 + 0,5256

 

Сравним получаемые по этой формуле теоретические величины   и реально наблюдаемые значения  , приведенные в табл. 7:

 

= 0,1165 + 0,5256× = 0,1165 + 0,5256×0,121 = 0,1802,

 

что отличается от наблюдаемого значения  = 0,110. Чтобы уровнять теоретическую и реальную величины, необходимо провести коррекцию теоретической величины  . Достигается это путем добавления к значению   ошибки  = 0,0702: (0,1802  0,0702 = 0,110).

Поскольку величины   и   случайные, то, скорее всего, и остальные теоретические значения  , получаемые с использованием уравнения линейной регрессии, будут отличаться от реально наблюдаемых величин  , приведенных в таблице 7. В этой связи величины   необходимо корректировать ошибкой  на каждом шаге расчета. Так как величины   и   случайные, то и значения ошибки  также должны представлять собой случайные величины. В итоге уравнение линейной регрессии для акции С должно иметь следующий вид:

 

 =  + ,

где:

– случайная ошибка.

 

В общем случае, если в портфель включено nакций, то для любой i-ой акции портфеля уравнение линейной регрессии выглядит следующим образом:

 

=   ,

 

где:

 – доходность i-ой акции портфеля за шаг t;

 – параметр регрессии, называемый коэффициентом «альфа»; показывает, какая часть доходности i-ой акции портфеля не связана с изменениями доходности рыночного портфеля  ;

 – параметр линейной регрессии, называемый коэффициентом «бета», показывающий чувствительность доходности i-ой акции портфеля к изменениям рыночной доходности  ;

 – доходность рыночного портфеля в момент t;

 – случайная ошибка, свидетельствующая о том, что реальные, действующие значения   и   отклоняются от линейной зависимости.

 

Уравнение  =   является основным в линейном регрессионном анализе и берется за основу в модели Шарпа. В линейном регрессионном анализе полагается, что средняя арифметическая (ожидаемая) величина ошибок наблюдения E( )=0, то есть фактические величины   в среднем равномерно распределяются выше и ниже значений, получаемых при линейной регрессии.

Параметр бета. Особое значение необходимо уделить параметру  , поскольку он определяет чувствительность доходности i-ой акции портфеля к изменениям рыночной доходности. Коэффициент   для каждой ценной бумаги показывает, на сколько процентов изменится доля  , определяемая воздействием рынка ( × ), при изменении рыночной доходности на 1%.

В общем случае, если  >1, то доходность данной ценной бумаги более чувствительная, подвержена большим колебаниям, чем рыночная доходность r_m. Соответственно, при  <1 ценная бумага имеет меньший размах отклонений доходностей r_j от средней арифметической (ожидаемой) величины E(r_i), чем рыночная доходность. В этой связи ценные бумаги с коэффициентом  >1 классифицируются как более рискованные, чем рынок в целом, а с  <1 - менее рискованными, чем рынок в целом.

Как показывают исследования, для большинства ценных бумаг коэффициент  >0, хотя могут встретиться ценные бумаги и с отрицательной величиной  . В последнем случае доходности этих ценных бумаг отрицательно коррелированны с доходностью рыночного портфеля. Следует учитывать, что и в случае отрицательных величин  , если величина этого коэффициента по модулю превосходит единицу, то есть   (например,  = 1,5), то акции считаются более рискованными, чем рынок в целом.

Поскольку коэффициент  характеризует зависимость доходности исследуемой акции и рыночного портфеля, то, очевидно, что данный коэффициент отражает только систематическую, недиверсифицируемую часть риска.

Определение параметров   и   регрессионной модели и оценка результатов регрессии. Для нахождения параметров   и   по результатам наблюдений используется метод наименьших квадратов (МНК). По этому методу в качестве параметров   и   берутся такие значения, которые минимизируют сумму квадратов ошибок  , то есть которых величина: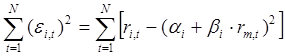

 



 

достигает минимума. Если провести необходимые вычисления, то окажется, что выражение имеет минимум, когда параметры   и   принимают следующие значения: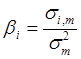

 



 



 

Если будут известны наблюдаемые в течение N лет величины   и  , то, пользуясь известными формулами для вычисления ожидаемых доходностей, ковариаций и дисперсий, можно найти E(r_i), E(r_m),  и  , подставить их в выше представленные формулы и вычислить параметры регрессии   и  .

Найдем значения коэффициентов   и  для акций «А», «В» и «С»:

 

=0,2494 и  = 0,9787

 

= 0,0117 и  =0,9470

 

= 0,1165 и  = 0,5256

 

Вычисление дисперсий случайной ошибки. Поскольку для определения оптимального портфеля с использованием модели Шарпа понадобятся значения дисперсий   случайных ошибок, то проведем необходимые вычисления. Общая формула для вычисления дисперсии случайной ошибки имеет вид: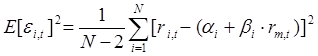

 

 = 

 

Для акций «А» вычисления дают:

 

=[(0,1200,2694+0,97870,1212) +(0,0400,2694+0,97870,2924) +(0,0100,2694+0,97870,1479) + и т.д. по всем 10 годам] / 8 = 0,0073

 

Соответственно:  =0,0136 и  =0,0375.

Для наглядности сведем данные регрессионного анализа для акций «А», «В» и «С» в одну таблицу (табл. 8):

 

Таблица 8.

 

Данные, полученные с использованием регрессионной модели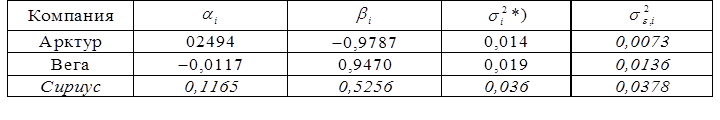

 



 

*) Вычислены ранее без регрессионных формул

 

Оценка результатов регрессии. Вычисленные параметры   и   регрессионной модели дают представление об общих тенденциях взаимосвязей между изменениями доходности рыночного портфеля   и доходностью   оцениваемой акции. Однако величины   и   не позволяют давать однозначный ответ о степени подобной взаимосвязи. Точность регрессионной модели, степень взаимосвязи   и   определяется разбросом случайных ошибок  , который можно оценить с помощью дисперсии случайной ошибки  . Кроме того, точность регрессии можно определить, оценивая, сколь точно регрессионная модель определяет дисперсию   доходности ценных бумаг, для которых составляется регрессионная модель.

Чуть ниже будет показано, что дисперсию i-ой ценной бумаги   можно представить в виде двух слагаемых:

 

 = 

 

Как видим, первое слагаемое свидетельствует, что часть риска i-ой ценной бумаги определяется нестабильностью самого рынка, поскольку туда входит   – дисперсия рыночной доходности r_m. Второе же слагаемое   показывает, что в суммарном риске ценной бумаги присутствует и собственная доля, не зависящая от колебаний рынка.

Разделим обе части равенства  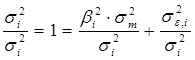 =   на величину  :

 



 

Обратим внимание, что в этом случае первое слагаемое будет показывать, какую долю в суммарном риске ценной бумаги можно описать с помощью регрессионной модели  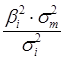=  , а второе слагаемое – степень неточности регрессионной модели. Значит, чем ближе величина   к единице, тем более точная регрессионная модель.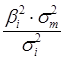

 – это квадрат коэффициента корреляции  . Именно квадрат коэффициента корреляции   является мерой оценки точности линейной регрессии, то есть мерой того, насколько точно уравнение регрессии подходит для описания соотношений реальных данных   и  .

Вычислим величину   для акций «А», «В» и «С», вспомнив ранее вычисленные значения  ;  ;  :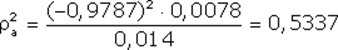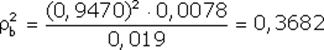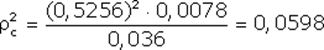

 



 



 



 

Эти данные свидетельствуют, что лучше всего линейная регрессия описывает поведение акций компании «А», так как величина   ближе к единице, чем для других компаний. Для компании «С» использование выбранного индекса РЦБ при составлении линейной регрессионной модели не оправданно, так как только 6% (0,0598) изменений ее доходности можно связать с колебаниями рынка.

 

Использование модели Шарпа для построения границы эффективных портфелей.

В основу модели Шарпа положена линейная регрессия. Для применения модели Шарпа необходимо предварительно ввести ряд условий. Если предположить, что инвестор формирует портфель из n ценных бумаг, то будем считать, что:

1)      Средняя арифметическая (ожидаемая) величина случайных ошибок = 0 для всех акций портфеля, то есть для i=1,2,...,n.

2)      Дисперсия случайных ошибок   для каждой ценной бумаги постоянна.

3)      Для каждой акции портфеля отсутствует корреляция между наблюдаемыми в течение N шагов расчета величинами случайных ошибок, то есть E[  ]= 0 (t=1,2,...,N).

4)      Отсутствует корреляция между случайными ошибками любых двух ценных бумаг в портфеле, иначе говоря, E[  ]=0.

5)      Отсутствует корреляция между случайными ошибками   и рыночной доходности, то есть   = 0.

 

Определение доходности и риска отдельной акции портфеля. Используя эти упрощения, можно получить выражения E(r_i),   и _i,j для любых акций в портфеле:

 

 =  +  

 

 =    + 

 

 =   

 

необходимые для построения границы эффективных портфелей. При этом инвестору требуется предварительно вычислить n значений  , n величин  , n значений  , а также   и  . Следовательно, всего потребуется найти: (n+n+n+2)=3n+2 начальных данных, что существенно меньше объема вычислений для модели Марковица. Например, при формировании портфеля из 30 ценных бумаг для определения границы эффективных портфелей надо 3×30+2=92 начальных данных по модели Шарпа и 495 (в 5 раз больше!) по модели Марковица.

Сокращение объема вычислений в модели Шарпа происходит потому, что все парные ковариации   между доходностями ценных бумаг в портфеле предполагаются равными нулю. А чтобы отразить взаимное влияние риска одной ценной бумаги на риск другой ценной бумаги, Шарп предложил свести эти ковариационные эффекты к взаимосвязи ценных бумаг портфеля с каким-то рыночным индексом, например, S&P500. Иначе говоря, корреляция между доходностями ценных бумаг в портфеле выражается с помощью рыночного индекса.

Определение ожидаемой доходности и дисперсии портфеля. Как установлено, ожидаемая доходность портфеля, состоящего из n ценных бумаг, вычисляется по формуле: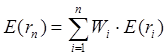

 



 

где

 – вес каждой ценной бумаги в портфеле.

 

Подставим в эту формулу выражение   из формулы  =  +   :

 

 = [ +  ]

 

Выделим в этом равенстве слагаемые, на которые не оказывает воздействие изменения рынка, и которые зависят от рыночных показателей:

 

=  + (  )

 

Для придания этой формуле компактности, Шарп предложил считать рыночный портфель в качестве условной (n+1)-ой акции портфеля. В таком случае, второе слагаемое уравнения  =  + (  )  можно представить в виде:

 

(  ) =  ( ),

 

где:

 =  

( ) = 

 

При этом считается, что дисперсия (n+1)-ой ошибки равна дисперсии рыночной доходности:   =  . Выражение   =    представляет собой сумму взвешенных величин «беты» ( ) каждой ценной бумаги (где весом служат  ) и называется портфельной бетой ( ).

С учетом выражений учетом выше сказанного формулу ожидаемой доходности портфеля можно записать так: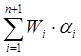

 

 = 

 

Итак, ожидаемую доходность портфеля E(rn) можно представить состоящей из двух частей:

а)      суммы взвешенных параметров   каждой ценной бумаги – W₁₁+W₂₂+...+W_n_n, что отражает вклад в E(rn) самих ценных бумаг, и

б)      компоненты W_n+1_n+1=(  ) , то есть произведения портфельной беты и ожидаемой рыночной доходности, что отражает взаимосвязь рынка с ценными бумагами портфеля.

 

Дисперсия портфеля. Как известно, дисперсию портфеля можно представить в виде:

 

 =    +   

 

Если вместо значений   и   подставить сюда выражения:

 

 =    + 

 

 =    ,

 

провести соответствующие вычисления и воспользоваться условиями (n+1) акции, то можно показать, что дисперсия портфеля представляется в виде:

 

 =  

 

При этом только необходимо иметь в виду, что W_n+1 =   , то есть (W_n+1) =(W₁₁+W₂₂+...+W_n_n) , а   =  . Значит, дисперсию портфеля, содержащего n акций, можно представить состоящей из двух компонент:

а)      средневзвешенных дисперсий ошибок   , где весами служат  , что отражает долю риска портфеля, связанного с риском самих ценных бумаг (собственный риск);

б)         – взвешенной величины дисперсии доходности рыночного портфеля  , где весом служит квадрат портфельной беты, что отражает долю риска портфеля, определяемого нестабильностью самого рынка (рыночный риск).

 

Исходя из изложенного, можно аналогично тому, как это делалось в предыдущей части, показать, что с увеличением числа ценных бумаг в портфеле первая часть риска портфеля (  ) будет стремиться к нулю. Поэтому диверсификация портфеля приводит к уменьшению риска, связанного с нестабильностью самих ценных бумаг, оставляя лишь компоненту   , зависящую от нестабильности самого рынка.

 

Формулирование цели инвестора в модели Шарпа. В модели Шарпа цель инвестора сводится к следующему:

необходимо найти минимальное значение дисперсии портфеля:

 

 

 

при следующих начальных условиях:

 

 

 

 

 

 

 

Отметим основные этапы, которые необходимо выполнить для построения границы эффективных портфелей в модели Шарпа:

1)      Выбрать n ценных бумаг, из которых формируется портфель, и определить исторический промежуток в N лет, за который будут наблюдаться значения доходности   каждой ценной бумаги.

2)      По рыночному индексу (например, РТС) вычислить рыночные доходности   для того же промежутка времени.

3)      Найти величины   и  :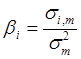

 



 

 =     

 

4)      Вычислить дисперсии   ошибок регрессионной модели.

5)      Решить с применением методов линейной алгебры задачу построения границы эффективных портфелей.

 

Рассмотрим пример построения границы эффективных портфелей, состоящих из акций «А», «В» и «С». Итак, задача инвестора в этом случае сводится к следующему: необходимо минимизировать выражение:

 

 

 

при следующих начальных условиях:

 



 



 



 

Подставим вычисленные ранее значения  ,  ,  ,   и   в эти выражения:

 



 



 



 



 

Для нахождения весов ценных бумаг   необходимо предварительно составить полином Лагранжа:

 



 



 

,

 

где

Г₁, Г₂, Г₃ – множители Лагранжа.

 

Затем берутся 7 частных производные полинома L по каждой из семи неизвестных W₁, W₂, W₃, W₄, а также Г₁, Г₂, Г₃ и приравниваются к нулю:

 

 = 0,0146W_a + 0,2494Г₁ + Г₂ - 0,9787Г₃ = 0

 

 = 0,0271W_b - 0,0117Г₁ + Г₂ + 0,9470Г₃ = 0

 

 = 0,0756W_c + 0,1165Г₁ + Г₂ + 0,5256Г₃ = 0

 

 = 0,0156W₄ + 0,1475Г₁ - Г₃ = 0

 

 = 0,2494W_a - 0,0117W_b + 0,1165W_c + 0,1475W₄ -  * =0

 

 = W_a + W_b + W_c = 0

 

 = -0,9787W_a + 0,9470W_b + 0,5256W_c - W₄ = 0

 

В матричной форме эти семь уравнений записываются в виде: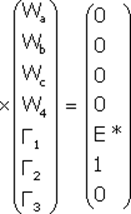

 



 



 

Представим это в виде матричного уравнения:

 



 

Чтобы найти веса  , необходимо вычислить на компьютере матрицу  , обратную матрице Т, и решить уравнение:  , то есть каждую строку обратной матрицы умножить на столбец Е.

 

Решение этой задачи дает следующие результаты:

 

W_А = -8,27683E* + 1,53921

 

W_В = -3,98884E* + 0,86352

 

W_С = 12,26567E* - 1,40273

 

W₄ = 10,76503E* - 1,42538

 

Веса для MVP портфеля вычисляются путем нахождения обратной матрицы  , где   – матрица без пятой строки и пятого столбца, соответствующих ограничению E*.

С использованием выражений для весов акций портфеля инвестор в состоянии построить границу эффективных портфелей, а затем определить оптимальный портфель.

 

Сравнение результатов модели Шарпа и Марковица. Модели Марковица и Шарпа дают различные выражения для весов ценных бумаг в эффективных портфелях, сформированных из одних и тех же акций «А», «В» и «С» при одинаковых начальных условиях.

При этом следует иметь в виду, что поскольку модель Шарпа является приблизительной, то вычисленные значения дисперсии портфеля менее точные, чем полученные с использованием модели Марковица, то есть портфели в модели Марковица имеют всегда более низкие значения дисперсии, чем портфели, созданные по модели Шарпа. Тем не менее эта разница не очень велика, поэтому можно считать, что модель Шарпа является удачным приблизительным вариантом построения эффективных портфелей.

 

Вопросы для самопровекри:

1.      Какие два параметра используются в модели Г. Марковица для оценки инвестором эффективности вложения денег в портфель акций?

2.      Что понимается под термином «эффективный рынок» в контексте модели Г. Марковица?

3.      Оптимальный портфель одинаков для всех инвесторов. Вы согласны?

4.      Можно ли риск портфеля выразить посредством стандартного отклонения?

5.      Что в конечном итоге требуется найти при оптимизации инвестиционного портфеля методом Марковица?

6.      Какие величины связывает между собой регрессионная модель У. Шарпа?

7.      Верно ли утверждение, что коэффициент α может свидетельствовать о степени чувствительности доходности конкретной акции к изменениям рынка?

8.      Что означает величина коэффициента β?

9.      Является ли дисперсия случайной ошибки величиной, равно нулю? единице?

10.  Что подразумевается под «n + 1» акцией в теории Шарпа?

 

Литература по теме:

 

Базовое учебное пособие:

1.  Аскинадзи В.М. Инвестиции: учебник для бакалавров / В.М. Аскинадзи, В.Ф. Максимова; Моск. гос. ун-т экономики, статистики и информатики. – М.: Юрайт, 2014. – 422 с.

 

Основная литература:

1.  Черняк В.З. Управление инвестиционными проектами [Электронный ресурс]: учебное пособие для вузов / Черняк В.З. – Электрон. текстовые данные. – М.: ЮНИТИ-ДАНА, 2015. – 364 c. – Режим доступа http://www.iprbookshop.ru/52060. – ЭБС «IPRbooks»

2.  Инвестиции / У.Ф. Шарп, Г.Д. Александер, Д.В. Бэйли; Пер. с англ. А.Н. Буренина, А.А. Васина. – М.: ИНФРА-М, 2012. – 1028 с.

 

Дополнительная литература:

1.  Гудков Ф.А. Инвестиции в ценные бумаги / Ф.А. Гудков. – М.: ИНФРА-М, 2014. – 160 c.

2.  Рынок ценных бумаг: учебник для бакалавров / Под общ. ред. Н.И. Берзона. – 3-е изд., перераб. и доп. – М.: Юрайт, 2015. – 537 с. – Серия: Бакалавр. Углубленный курс.

 

Интернет-ресурсы:

1.  http://www.cfin.ru/

2.  http://www.finam.ru/

3.  http://www.pro-invest.com/

4. http://www.rbc.ru/