Введение 1 Наука о сопротивлении материалов
 Скачать 4.19 Mb. Скачать 4.19 Mb.
|
1.6 Внутренние усилия. Виды нагруженийДействие внешних сил вызывает изменение взаимного положения частиц материального тела. Перемещение частиц влечёт за собой изменение в силах взаимодействия между ними. Эти силы называют внутренними. Внутренние силы и по величине и по характеру воздействия соответствуют деформации тела, т.е. являются следствием результата действия внешних сил. Внутренние усилия определяют методом сечений. Рассмотрим тело, находящееся под действием системы внешних сил в равновесии ( рис1.11). Мысленно рассекая тело плоскостью, отбросим любую из двух полученных частей. Заменим действие отброшенной части внутренними усилиями. Поскольку тело в целом находится в равновесии, в равновесии находится и любая его часть. Характер распределения внутренних усилий неизвестен. В соответствии с принципами теоретической механики, любую систему сил можно привести к главному вектору Внутренние силовые факторы могут быть определены из условий равновесия рассматриваемой части материального тела 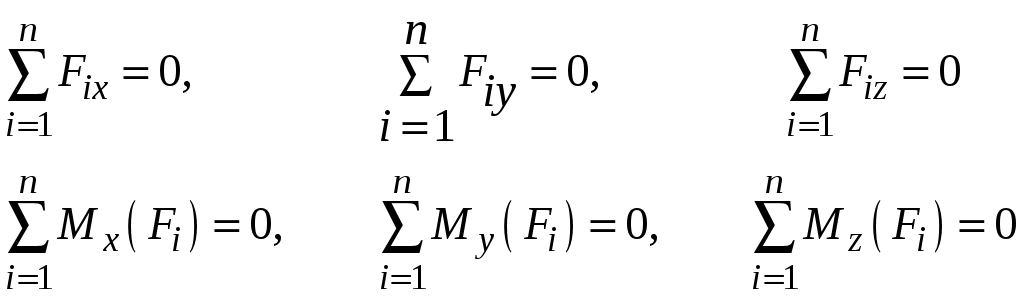 (1.1) (1.1)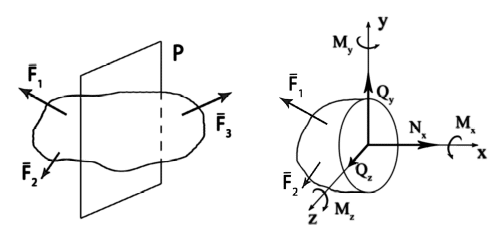 а). б). Рис 1.11 В зависимости от того, какие внутренние силовые факторы имеют место в сечении, различают виды нагружения. Растяжение, сжатие − такой вид нагружения, при котором Сдвиг, срез имеет место тогда, когда в поперечном сечении силы Кручение − такой вид нагружения, при котором в поперечном сечении имеет место только крутящий момент Изгиб − вид нагружения, при котором 1.7 НапряженияНапряжение есть интенсивность распределения внутренних усилий по сечению, или внутреннее усилие, приходящееся на единицу площади поперечного сечения. В общем случае нагружения закон распределения внутренних усилий неизвестен, однако в окрестности бесконечно малого элемента можно считать внутреннее усилие распределённым равномерно. Равнодействующая внутренних сил на площадке Предел отношения В общем случае вектор Проекцию вектора 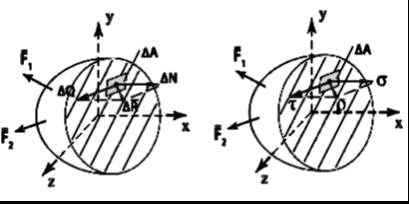 а) б) Рис.1.12 Размерность напряжения − паскаль (Па) Совокупность напряжений, действующих в рассматриваемой точке по различным направлениям, называется напряженным состоянием в точке. |
