Введение 1 Наука о сопротивлении материалов

• Название: Введение 1 Наука о сопротивлении материалов
• Дата: 24.08.2022
• Размер: 4.19 Mb.
• Имя файла: konspektlekciisoprotivleniematerialov.doc
• Тип: Лекция; #651978
• страница: 6 из 12

2.5 Учёт влияния собственного веса

Влияние собственного веса оказывается существенным в элементах большой протяженности. Собственный вес это нагрузка, распределенная по объему стержня. Интенсивность этой нагрузки – величина удельного веса .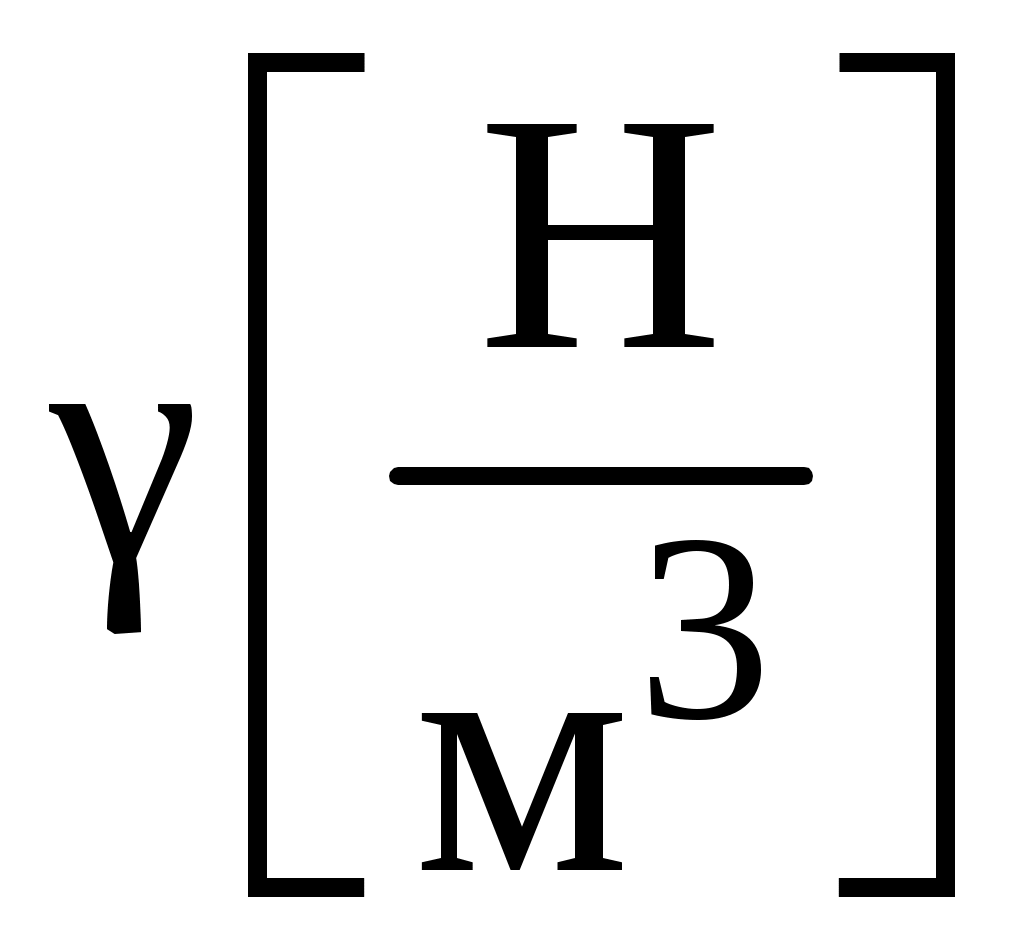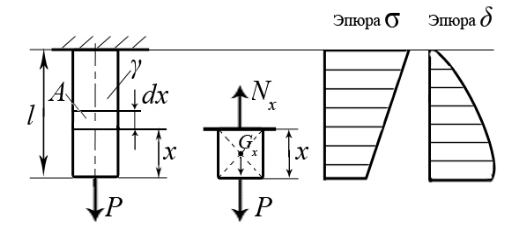



а) б) в) г)

Рис.2.8

Внутреннее усилие в сечении, находящемся на расстоянии x от свободного конца стержня, получаем исходя из условия равновесия отсеченной части:

. (2.12)

Напряжение в сечении x равно:

, (2.13)

что указывает на линейный характер распределения напряжений вдоль оси стержня (рис.2.8,б) . При х = 0 напряжение: . Величина напряжения максимальна в месте заделки при x = l:



Эпюра напряжений с учетом собственного веса представлена на рис.2.8,в.

При оценке деформаций с учетом собственного веса следует отметить, что деформации, так же как напряжения, переменны по длине стержня. Рассмотрим деформацию бесконечно малого участка длиной dx(рис.2.8,а). В соответствии с законом Гука



Перемещение свободного конца δ равно удлинению стержня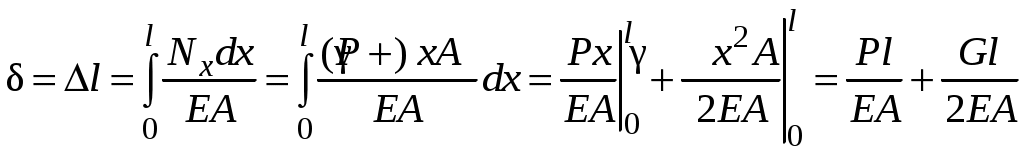



Здесь − собственный вес стержня.

2.6 Расчёт статически неопределимых систем

В ходе предыдущих рассуждений внутренние усилия определялись методом сечений с использованием уравнений равновесия системы. Системы, в которых число неизвестных превышает число уравнений статики, называют статически неопределимыми.

Решение такого рода задач требует анализа картины возможных перемещений. Рассмотрим решение статически неопределимых задач на примере.

Пример 3. Ступенчатый брус жестко закреплен по концам и нагружен продольной силой P(рис.2.9,а).

Построить эпюры внутренних усилий, напряжений и перемещений имеющих место в системе.

Прежде чем определять внутренние усилия, необходимо выявить все внешние силы, действующие в системе. Кроме активной нагрузки P на стержень действуют две опорные реакции R_А и R_В, направленные вдоль оси стержня. Таким образом, прежде всего, необходимо определить неизвестные R_А и R_В.

Для равновесия такой системы сил необходимо и достаточно соблюдения условия: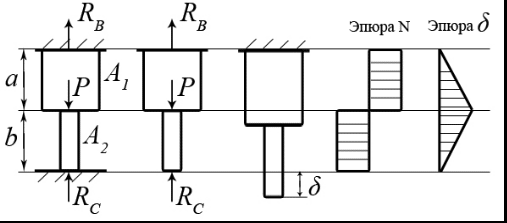





а) б) в) г) д)

Рис. 2.9

Число неизвестных – два, число уравнений статики – одно. Задача статически неопределима.

Необходимо составить еще одно дополнительное уравнение. Для этого отбросим «лишнюю» связь – опору C, заменив ее действие силой R_С(рис.2.9,б). При этом становится возможным перемещение свободного конца (рис.2.9,в):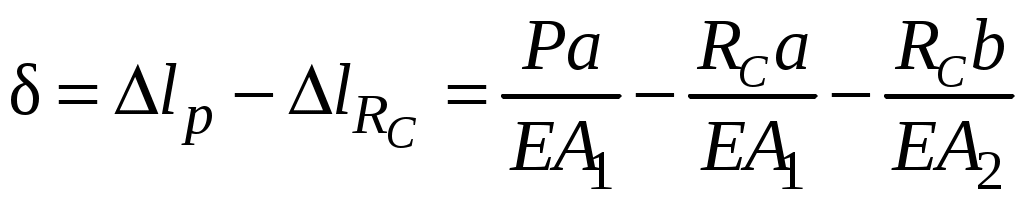



Однако, по условию задачи, это невозможно. Записывая это условие в математической форме, получаем дополнительное уравнение .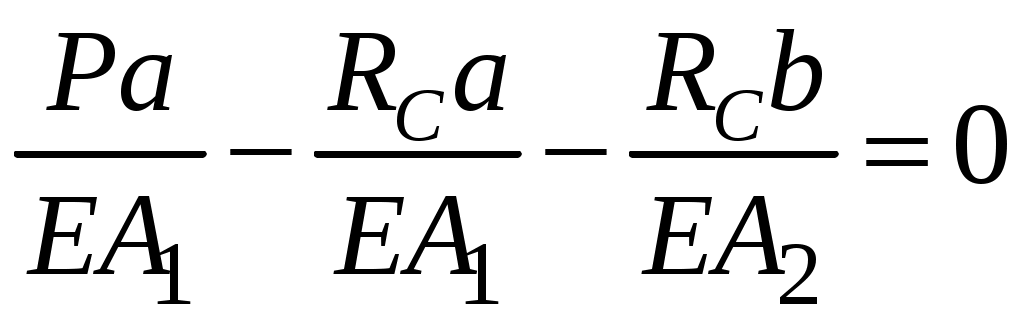

Полученное уравнение называется уравнением совместности деформаций. Решая его совместно с уравнением равновесия , определяют опорные реакции. Далее определяют внутренние усилия, перемещения и отражают это построением эпюр N и δ (рис 2.9,г,д).

Лекция3