Введение 1 Наука о сопротивлении материалов
 Скачать 4.19 Mb. Скачать 4.19 Mb.
|
4.2 Общие свойства геометрических характеристикВыше перечислены все основные геометрические характеристики плоских сечений, влияющие на прочность и жёсткость элементов конструкций и сооружений. В случае сложного составного сечения их можно определить, суммируя соответствующие характеристики простейших составляющих, на которые можно разбить сложное сечение. 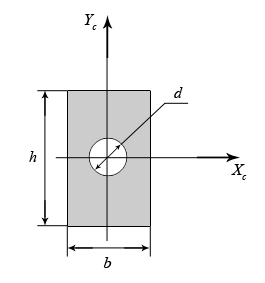 Рис. 4.3 Рассмотрим прямоугольное сечение с отверстием диаметром d по центру (рис.4.3). Оси Площадь поперечного сечения равна разности составляющих его: 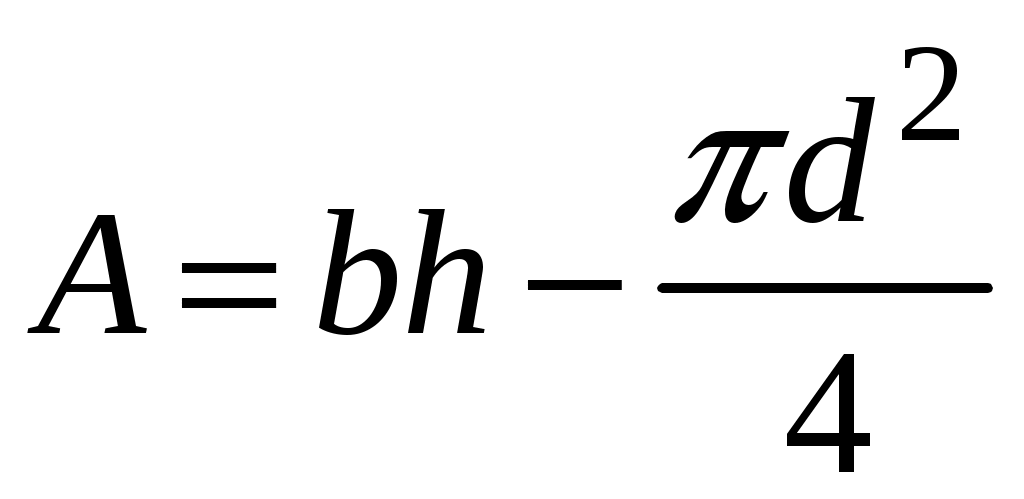 (4.6) (4.6)Статический момент сечения относительно центральных осей всегда равен нулю: 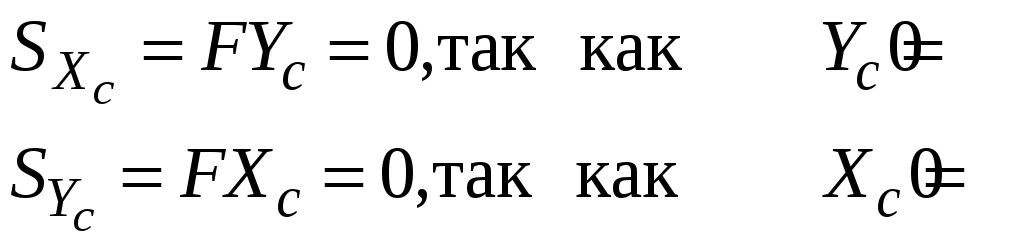 (4.7) (4.7)Осевые моменты инерции сложного сечения также можно определить как сумму или разность моментов инерции простейших составляющих: 4.3 Моменты инерции простейших геометрических фигурКруг Определяя геометрические характеристики круглого сечения диаметром d(рис.4.4), выделим бесконечно тонкое кольцо радиусом ρ, толщиной dρ. Элементарная площадь кольца 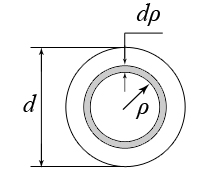 Рис. 4.4 Полярный момент инерции крулого сечения: 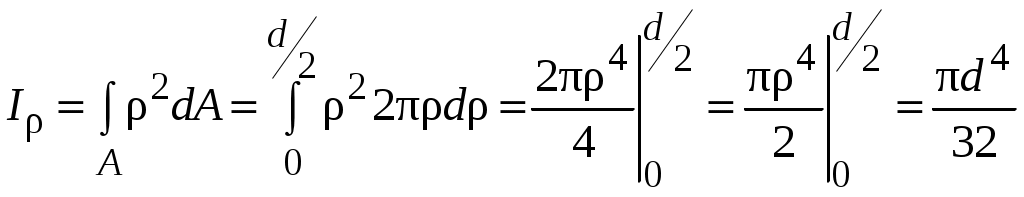 (4.9) (4.9)Известно, что 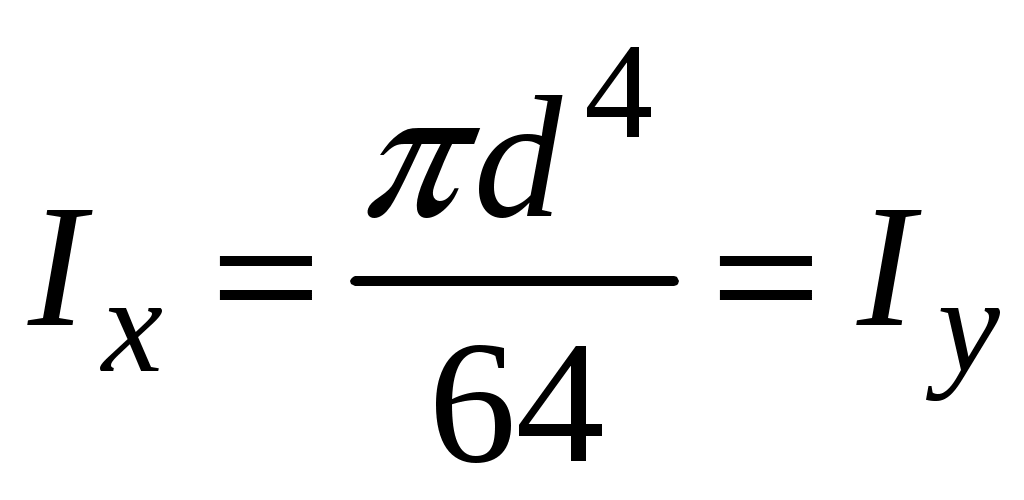 (4.10) (4.10)Прямоугольник 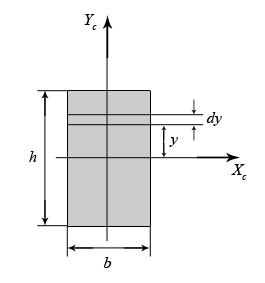 Рис. 4.5 Выделим элементарную площадку шириной b, толщиной dy. Определим момент инерции прямоугольного сечения относительно осиXc 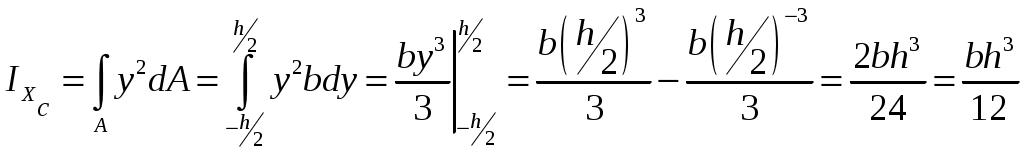 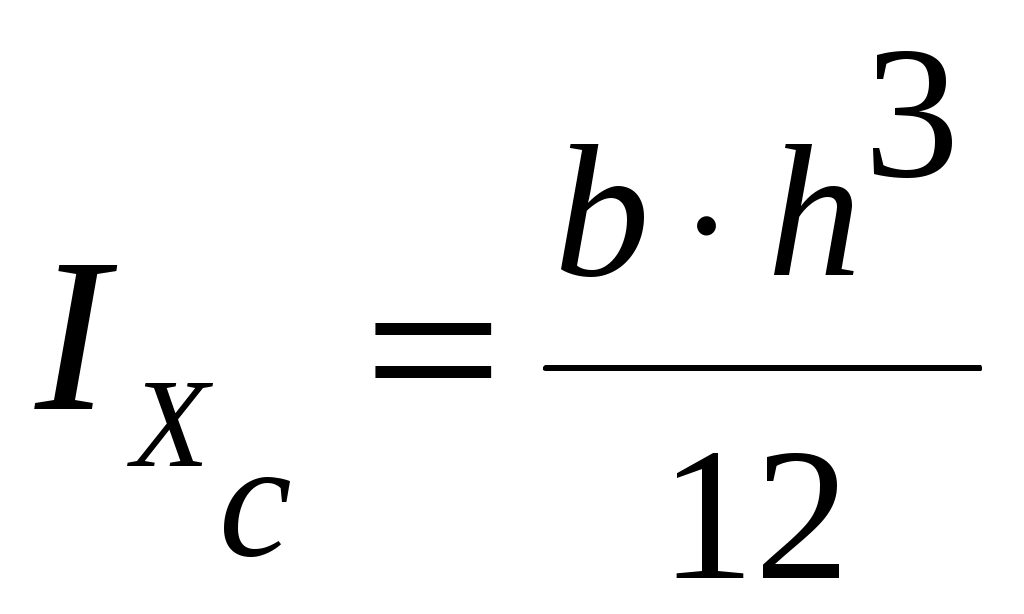 , очевидно , очевидно 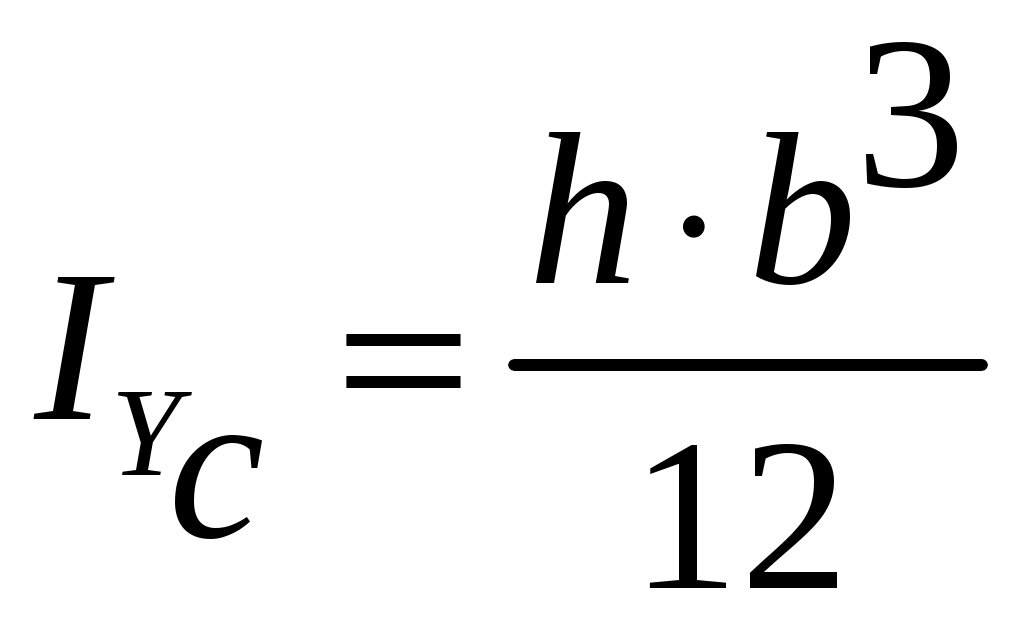 (4.11) (4.11)Квадрат 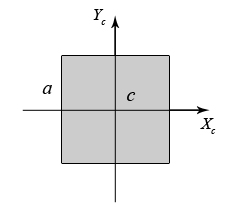 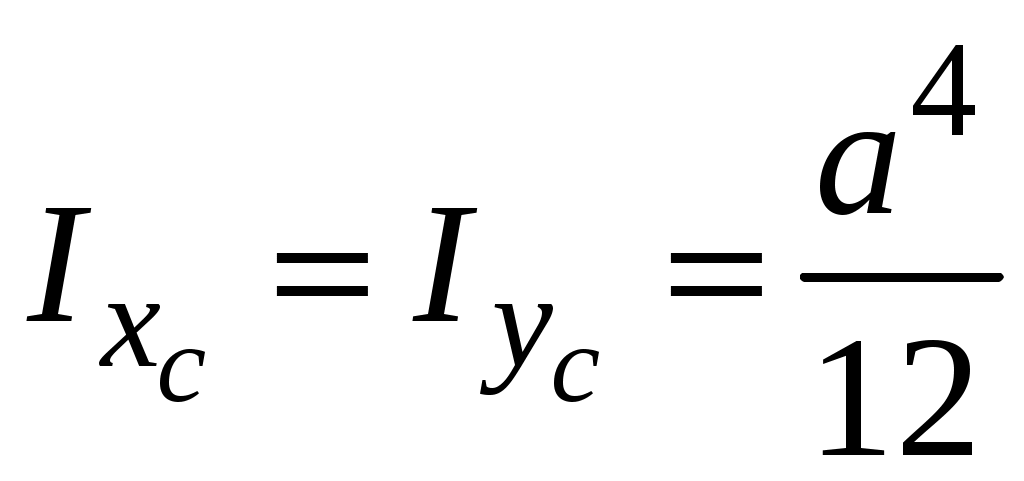 (4.12) (4.12)Рис.4.6 4.4 Моменты сопротивленияХарактеристики сечений, которые часто встречаются в расчётных соотношениях на прочность, зачастую записываются в форме 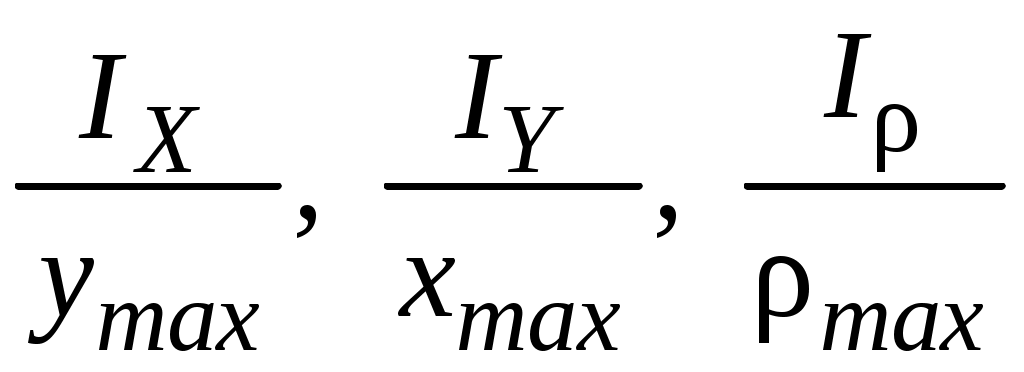 . Это соотношение рассматривается как вспомогательная геометрическая характеристика, называемая моментом сопротивления. Осевые моменты сопротивления сечения . Это соотношение рассматривается как вспомогательная геометрическая характеристика, называемая моментом сопротивления. Осевые моменты сопротивления сечения 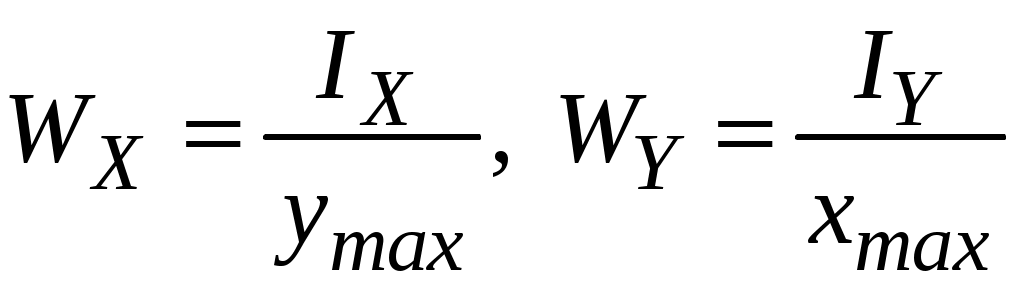 , полярный момент сопротивления , полярный момент сопротивления 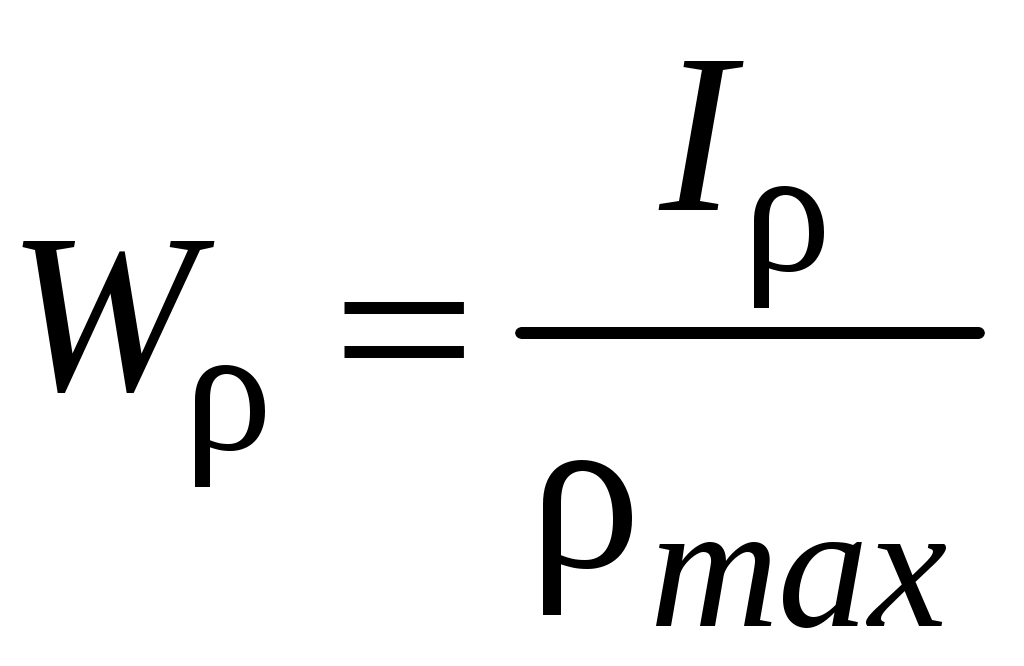 . Здесь . Здесь Моменты сопротивления простейших сеченийП 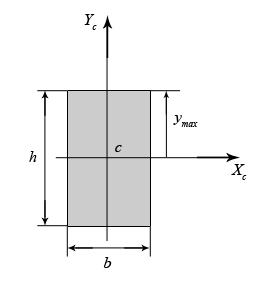 рямоугольник рямоугольник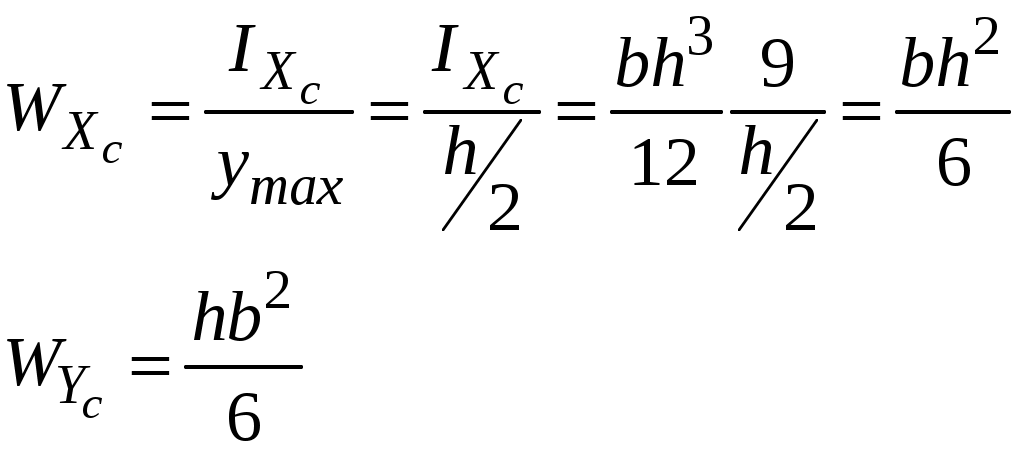 (4.13) Рис. 4.7 Круг 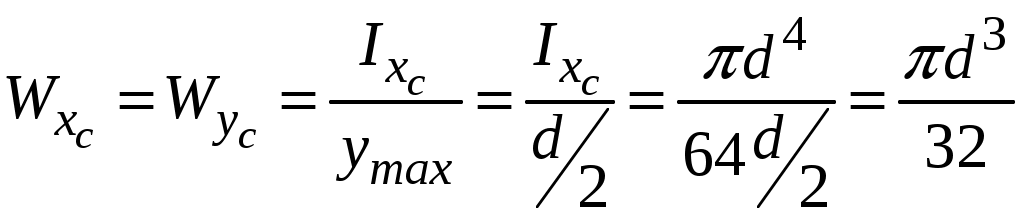  Полярный момент сопротивления 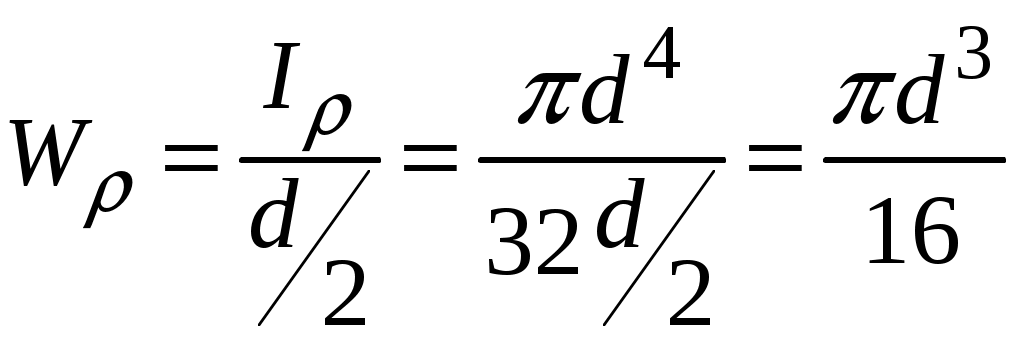 (4.14 ) Рис. 4.8 С 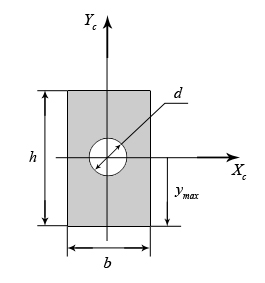 оставное сечение оставное сечениеМомент сопротивления такого сечения относительно оси 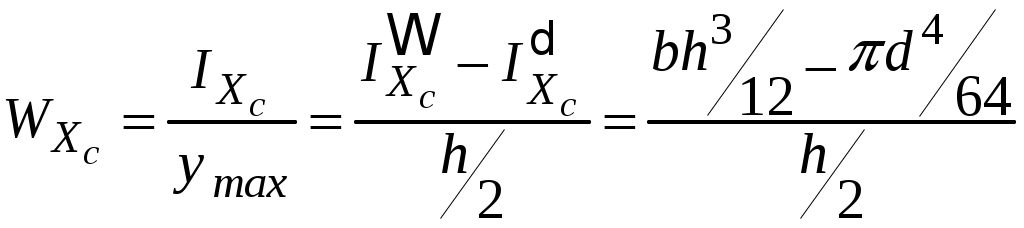 , ,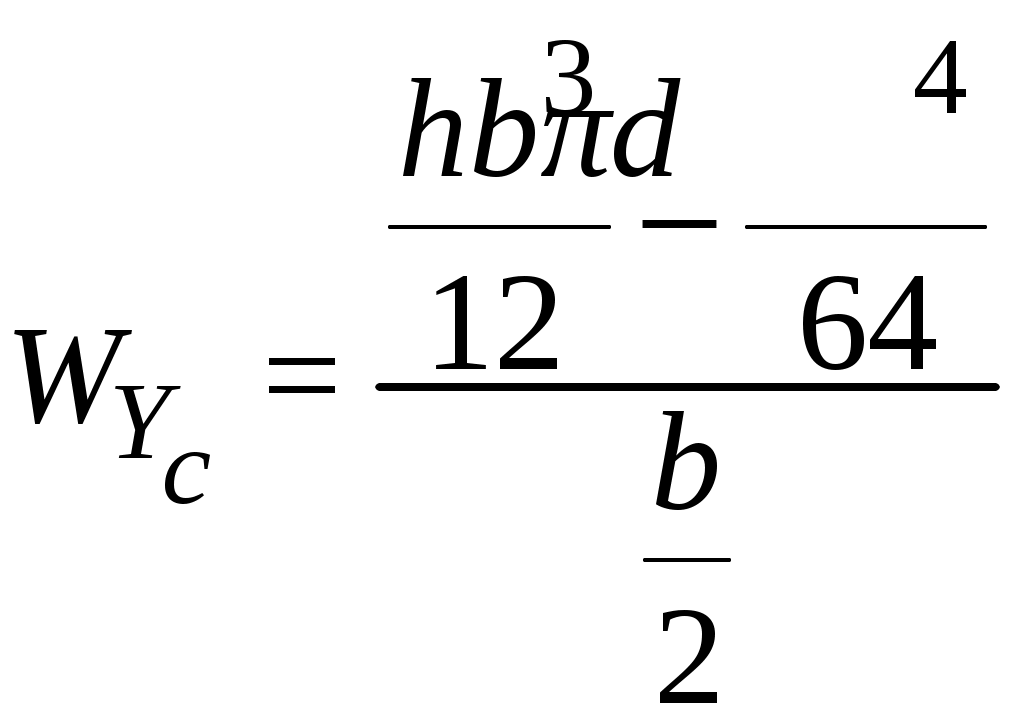 (4.15) (4.15)Рис. 4.9 4.5 Зависимость между моментами инерции относительно параллельных осей, одна их которых центральная Рассмотрим сечение, центральная ось которого 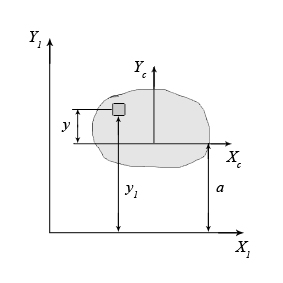 Рис. 4.10 Для доказательства сказанного следует выразить момент инерции относительно оси 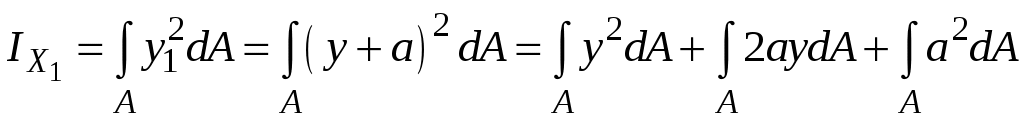 . .Здесь |
