Введение 1 Наука о сопротивлении материалов

• Название: Введение 1 Наука о сопротивлении материалов
• Дата: 24.08.2022
• Размер: 4.19 Mb.
• Имя файла: konspektlekciisoprotivleniematerialov.doc
• Тип: Лекция; #651978
• страница: 5 из 12

2.3 Деформации и перемещения при растяжении, сжатии

Деформацией называют изменения формы и размеров тела под действием внешних сил.

Рассмотрим цилиндрический стержень, нагруженный силами P.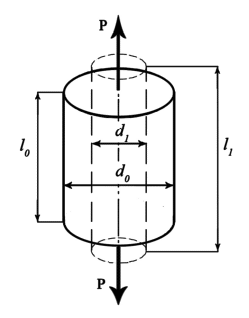



Рис.2.5

Исходные размеры стержня: длина l₀, диаметр d₀. После нагружения стержень остался цилиндрической формы, но размеры его изменились (рис.2.5). Новая его длина l₁, диаметр поперечного сечения d₁. При нагружении стержня имеет место абсолютная продольная деформация – изменение длины Δl = l₁-l₀, и абсолютная поперечная деформация – изменение диаметра Δd = d₀-d₁.

О степени деформирования нельзя судить только по величине абсолютных деформаций, так как они зависят не только от нагрузки, но и от первоначальных размеров стержня.

Характеристикой степени деформирования являются: относительная продоль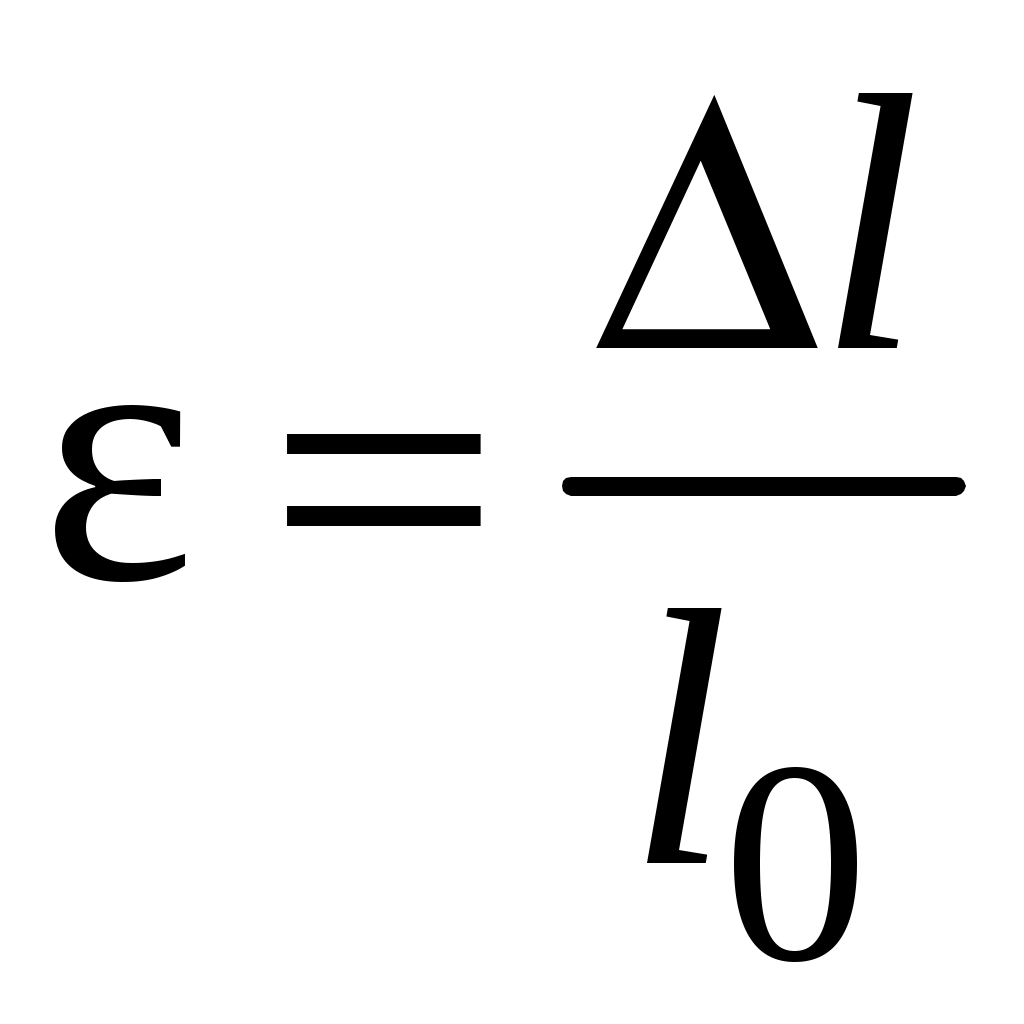ная деформация и относительная поперечная деформация 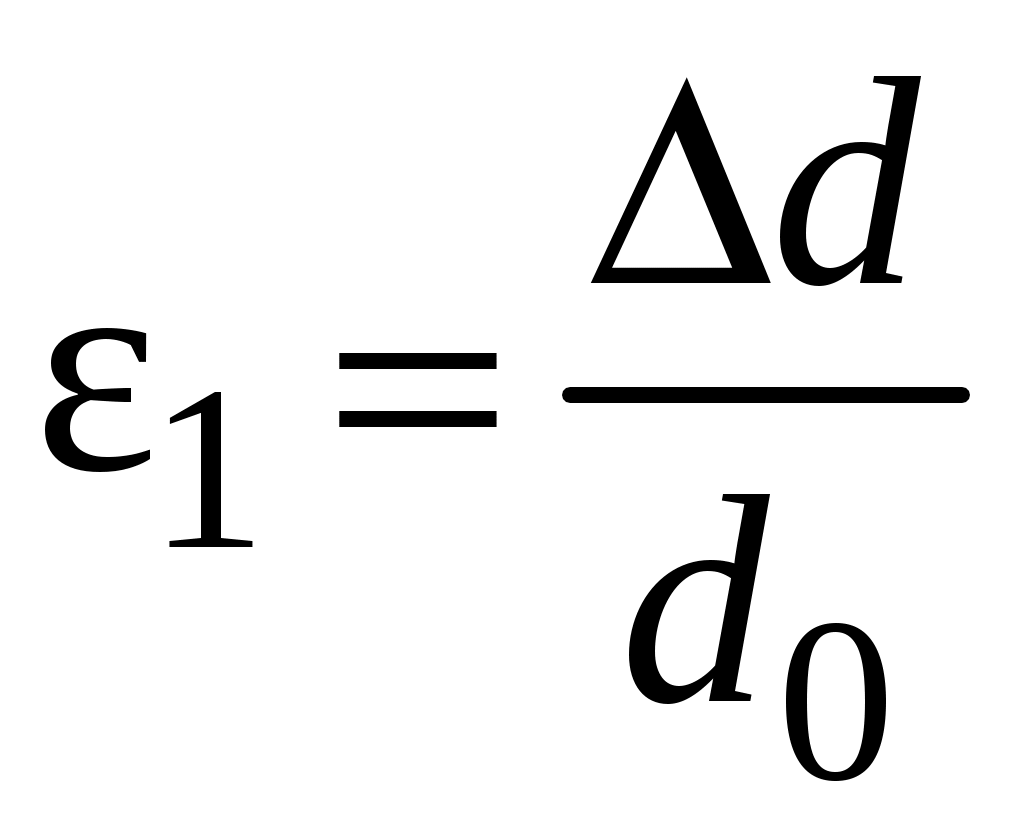. При упругом деформировании существует связь:

( 2.9)

Коэффициент пропорциональности μ называется коэффициентом Пуассона и является одной из упругих констант материала.

Значения коэффициента Пуассона

Таблица 2.2

Сталь 3	μ = 0,25÷0,35
Чугун серый	μ = 0,23÷0,27
Алюминий	μ = 0,32÷0,36
Каучук	μ = 0,47-0,50

2.4 Связь между напряжением и деформацией

В пределах упругого деформирования между напряжением и относительной продольной деформацией существует прямо пропорциональная зависимость, установленная Робертом Гуком

− закон Гука (2.10)

Коэффициент пропорциональности Е зависит от свойств материала, является упругой его константой и называется модулем упругости I рода или модулем Юнга.
Значения модуля упругости Е

Таблица 2.3

Сталь	Е = (2,0÷2,1)105 МПа
Чугун	Е = (1,2÷1,6)105 МПа
Алюминий	Е = 0,69·105 МПа
Дерево вдоль волокон	Е = (0,10÷0,12)105 МПа
Каучук	Е = 0,00008·105 МПа

Закон Гука может быть записан и в форме, используемой для расчета абсолютной продольной деформации. Учитывая, что 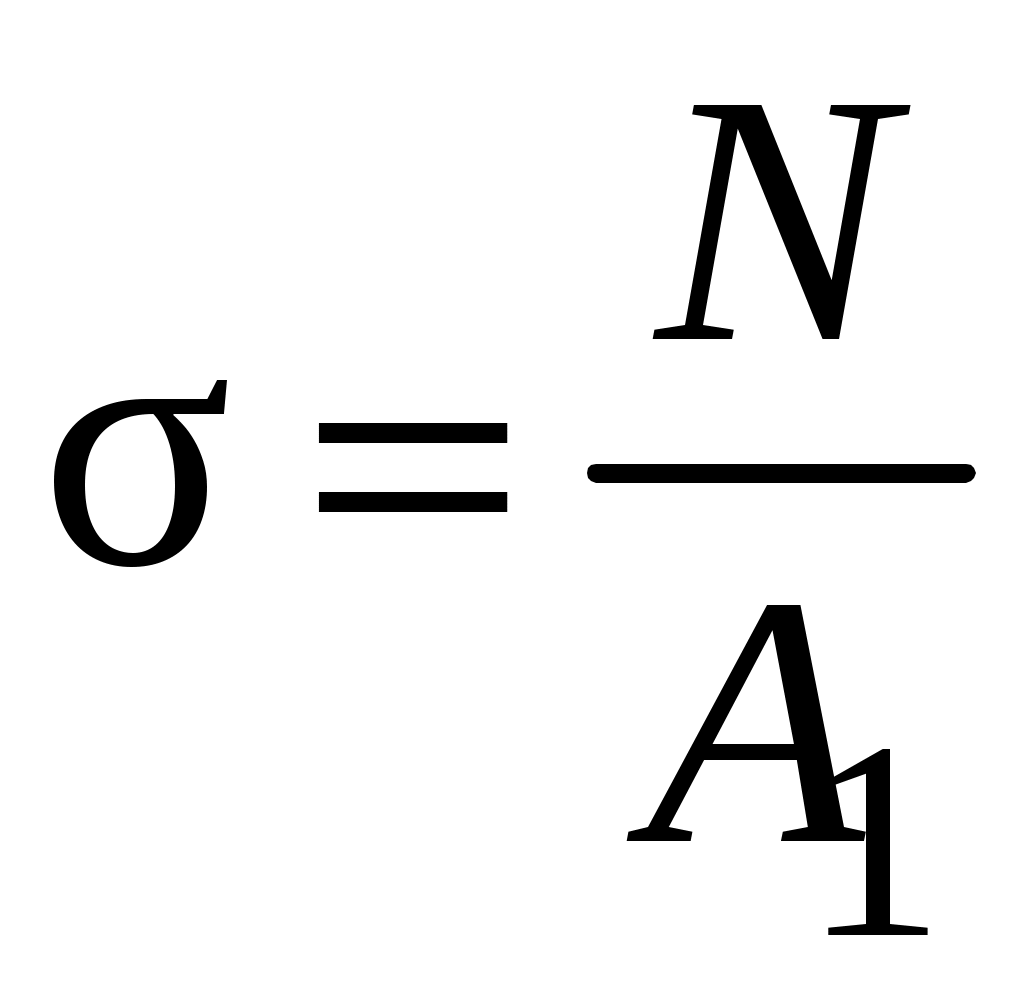, а подставляем в соотношение (2.9) и получаем:

(2.11)

Перемещения являются следствием деформаций.

Пример 2. Определить перемещение узла В шарнирно-стержневой системы, изображенной на рисунке рис2.6.

В силу геометрической и силовой симметрии узел В переместится вертикально вниз в положение В₁.

Н 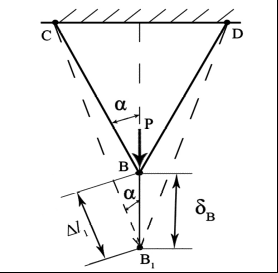а рис2.6 изображена картина возможных перемещений всех элементов системы.

СВ − исходное положение стержня;

СВ₁ − положение стержня после нагружения;

Δl₁ − изменение длины стержня 1, которое можно рассчитать, используя закон Гука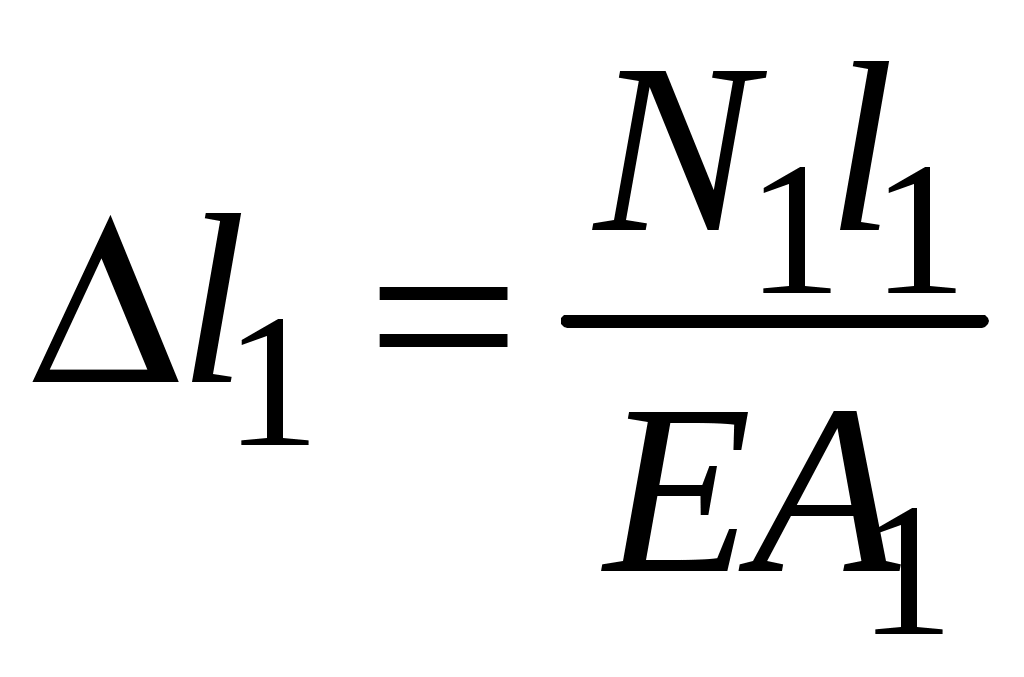

.
Рис.2.6 В силу малости упругих деформаций изменением угла α можно пренебречь. Определяем перемещение узла В исходя из геометрии картины возможных перемещений: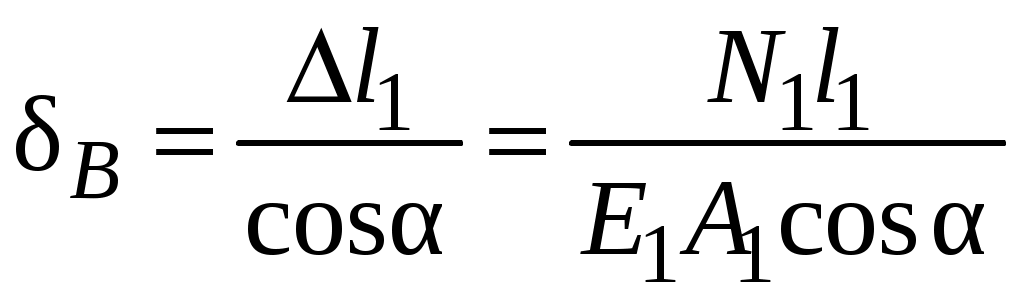



Пример 3. Определить перемещение сечений I-I и II-II ступенчатого бруса, нагруженного силой Р (рис. 2.7,а)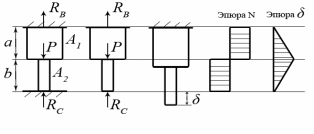



а) б) в)

Рис 2.7

Здесь A₁, A₂ − площади поперечного сечения соответствующих участков. Используя метод сечений, легко установить, что внутренние усилия на участках a и b равны силе P и являются растягивающими. Эпюра внутренних усилий представлена на рис.2.7,б

Перемещение в опорном сечении невозможно, то есть равно нулю. Перемещение сечения I-I зависит от деформации участка а.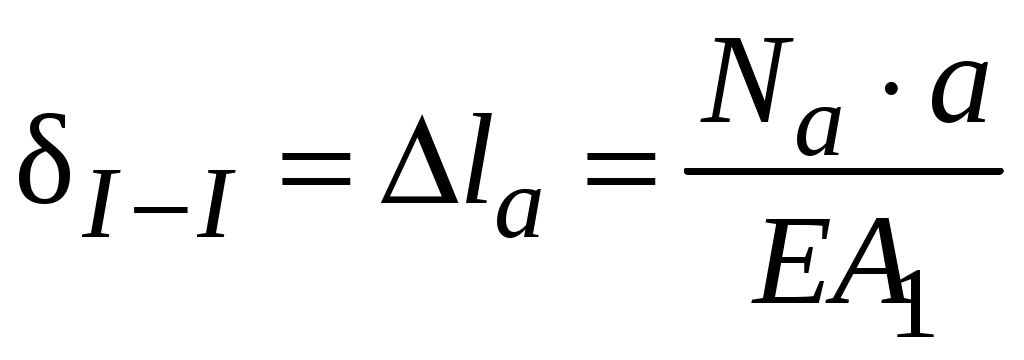



Перемещение сечения II–II есть следствие деформации обоих участков: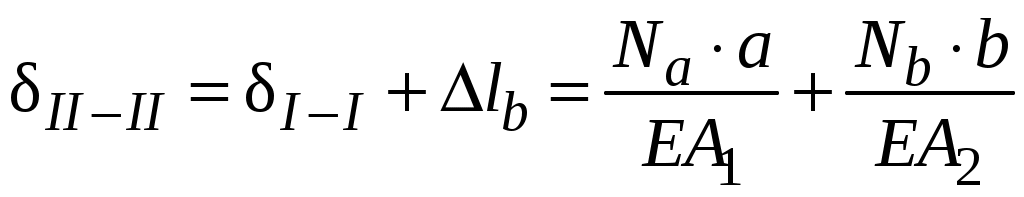



Откладывая полученные значения перемещений в масштабе в виде отрезков перпендикулярных оси, параллельной оси бруса, соединяем концы отрезков прямыми линиями. Эпюра перемещений представлена на рис. 2.7,в