Введение 1 Наука о сопротивлении материалов
 Скачать 4.19 Mb.
|
Расчёт сварных соединенийСварка является наиболее современным способом соединения элементов стальных конструкций. При соединении внахлёстку применяют лобовые (рис. 3.5,а) и фланговые (рис. 3.5,б) швы. И те и другие швы работают на срез. Расчёт на срез ведётся в предположении о равномерном распределении касательных напряжений по площади среза. При качественном выполнении сварного соединения разрушение шва идёт в направлении под углом 45° к катету шва. Катет шва выполняется равным толщине привариваемого листа t (рис. 3.6). 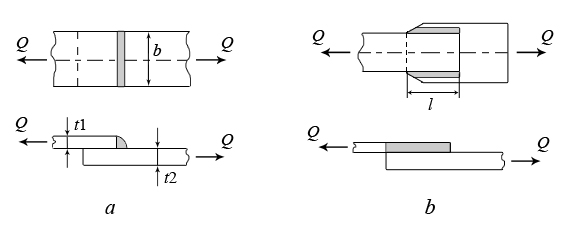 Рис. 3.5 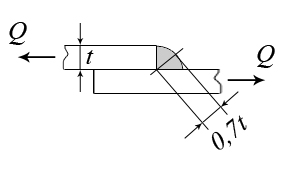 Рис. 3.6 Условие прочности сварного шва: 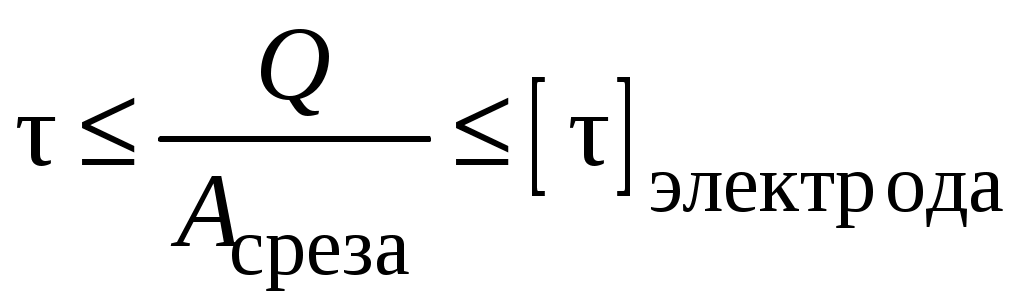 Для лобового шва  , для фланговых  ,  − допускаемое напряжение для материала электрода.Соединение двух листов может быть выполнено и встык (рис. 3.7). В этом случае зазор между соединяемыми листами заполняется . 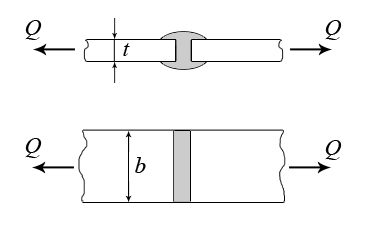 Рис. 3.7 расплавленным металлом. В таком соединении шов работает на растяжение. Условие прочности соединения:  Лекция 4.Геометрические характеристики плоских сеченийПрочность элементов конструкций зависит от свойств материала, из которого изготовлен элемент, от размеров его поперечного сечения. Однако очевидно, что прочность элемента в условиях изгиба (рис. 4.1) будет выше, если поперечное сечение его будет занимать положение I. 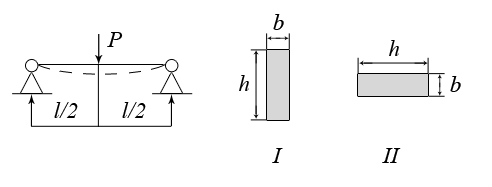 Рис. 4.1 При одной и той же площади поперечного сечения балка, закреплённая на двух опорах, прогнётся меньше, если поперечное сечение её занимает положении I. Напрашивается вывод, что на прочность и жёсткость оказывает влияние не только непосредственно площадь поперечного сечения элемента, но и другие геометрические характеристики сечения. 4.1 Виды геометрических характеристик Рассмотрим произвольное плоское сечение площадью А в системе отсчёта YoX (рис. 4.2). Любая из геометрических характеристик сечения может быть представлена в виде интегральной функции 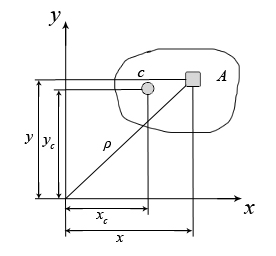 или   .Рис.4.2 При n = 0 получается площадь сечения, так как  . При n = 1 будет получен статический момент площади относительно оси X или Y  (4.1)Интегрируя можно убедиться, что статический момент площади относительно оси равен произведению площади на расстояние от центра тяжести сечения с до рассматриваемой оси:  (4.2)Здесь  − координаты центра тяжести сечения. Из выражений (4.2) следует, что статический момент сечения относительно оси, проходящей через центр тяжести, равен нулю.Эта характеристика помогает определить положение центра тяжести сложного составного сечения. Размерность статического момента − см3 или м3; он может быть как положительным, так и отрицательным. При n = 2 интегралы произведения элемента площади dA на квадрат расстояния его до осей представляют осевые моменты инерции  (4.3)Размерность осевых моментов инерции − см4, м4; они всегда положительны. Если под интегралом произведение элемента площади на квадрат расстояния его до точки О (полюса), получается характеристика называемая полярным моментом инерции  (4.4)Подставляя в (4.4) 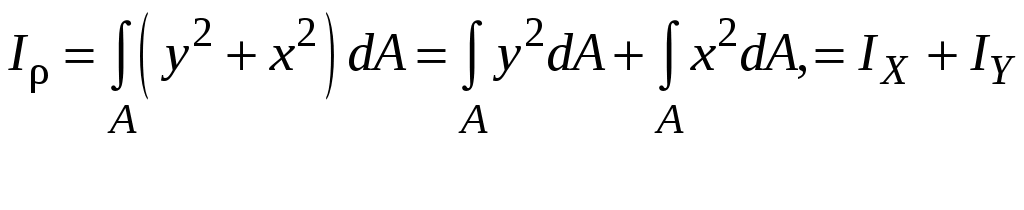 , получаем связь между осевыми и полярным моментом инерции сечения:  (4.5) Интегральная функция вида  позволяет оценить ещё одну геометрическую характеристику центробежный момент инерции сечения. Центробежный момент инерции может быть положительным, отрицательным и, даже, равным нулю. Оси, относительно которых центробежный момент инерции сечения равен нулю, называют главными. Осевые моменты инерции относительно главных осей достигают экстремальных значений. |