Введение 1 Наука о сопротивлении материалов
 Скачать 4.19 Mb. Скачать 4.19 Mb.
|
|
8. Действие динамических нагрузок При изучении статики считалось, что нагрузки растут от нуля до конечных значений достаточно медленно, поэтому ускорения, приобретаемые элементами конструкций, малы. Однако весьма часто нагрузки имеют динамический характер, так как изменяются с большой скоростью. Общий метод расчета на динамическую нагрузку основан на принципе Даламбера: всякое движущееся тело можно рассматривать в состоянии мгновенного равновесия, если к действующим силам добавить силу инерции, равную произведению массы на ускорение и направленную в сторону, противоположную ускорению. Равноускоренное движение Во многих случаях ускорения, с которыми перемещаются детали конструкции, постоянны. Динамические напряжения в этих случаях вычисляются без труда. П 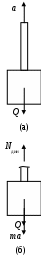 ример 1. Груз весом Q поднимают вверх с ускорением a. Определить напряжение в канате, рис. (а). ример 1. Груз весом Q поднимают вверх с ускорением a. Определить напряжение в канате, рис. (а).Решение. Прикладываем к грузу силу инерции 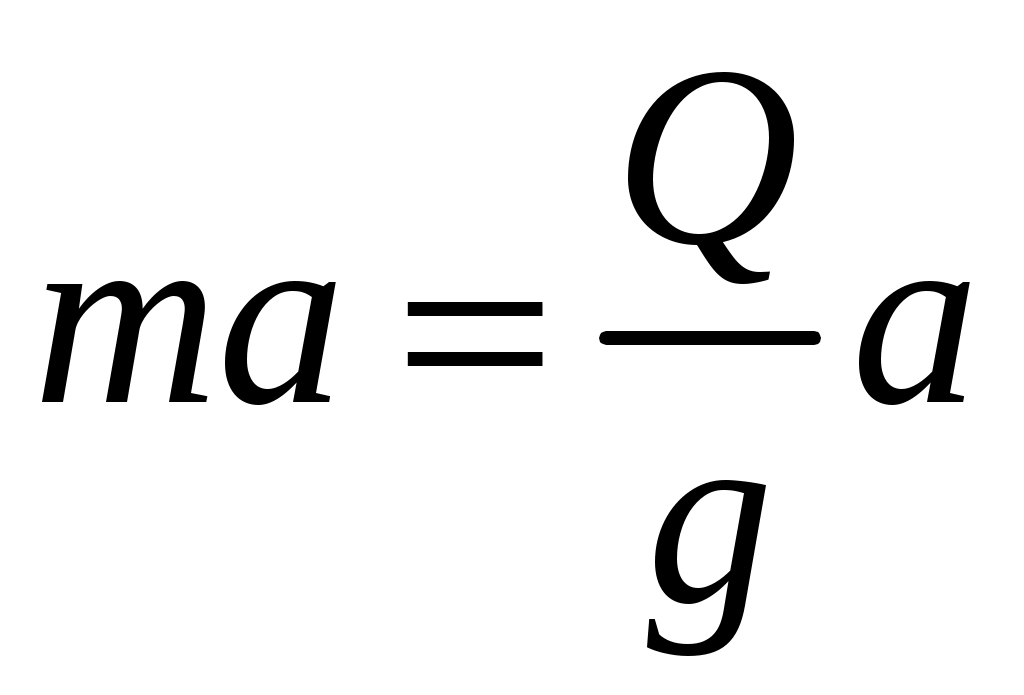 , направленную вниз. Делаем разрез и отбрасываем верхнюю часть, рис. (б). Усилие в канате Nдин: , направленную вниз. Делаем разрез и отбрасываем верхнюю часть, рис. (б). Усилие в канате Nдин:Проецируя все силы на вертикальную ось, получим 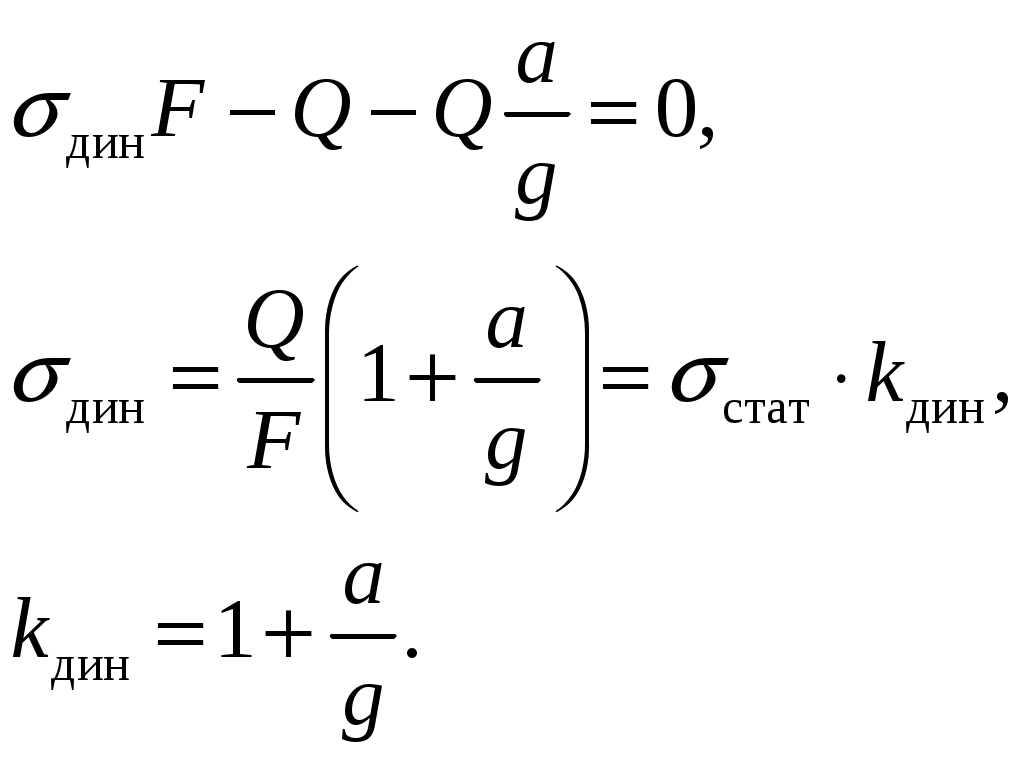 Таким образом, динамические напряжения могут быть вычислены через статические напряжения и коэффициент динамичности. Пример 2. Стержень с погонным весом q поднимают с помощью двух нитей с ускорением a. Определить напряжения в стержне. Р 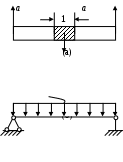 ешение. Прикладывая к единичному элементу стержня силу инерции ешение. Прикладывая к единичному элементу стержня силу инерции 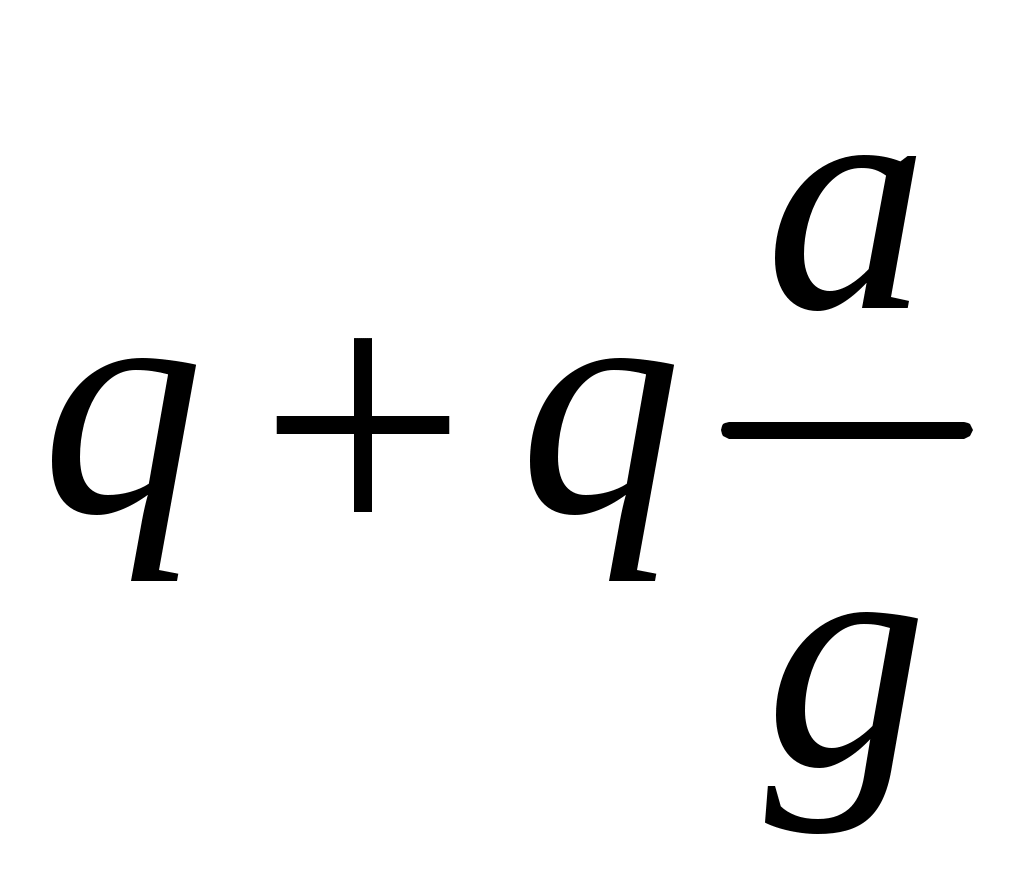 , рис. (б). Максимальный момент будет в сечении посредине балки: , рис. (б). Максимальный момент будет в сечении посредине балки: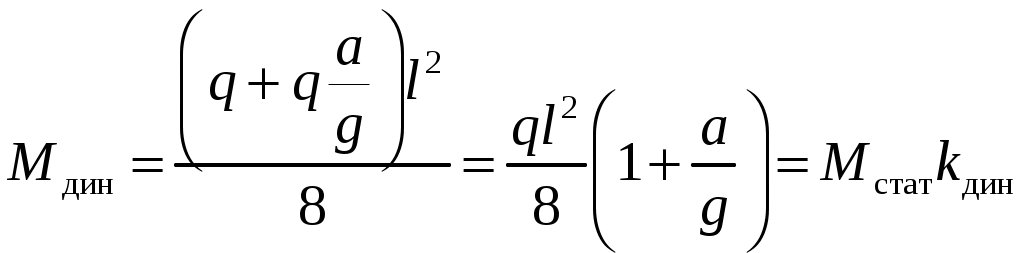 . .Максимальное напряжение 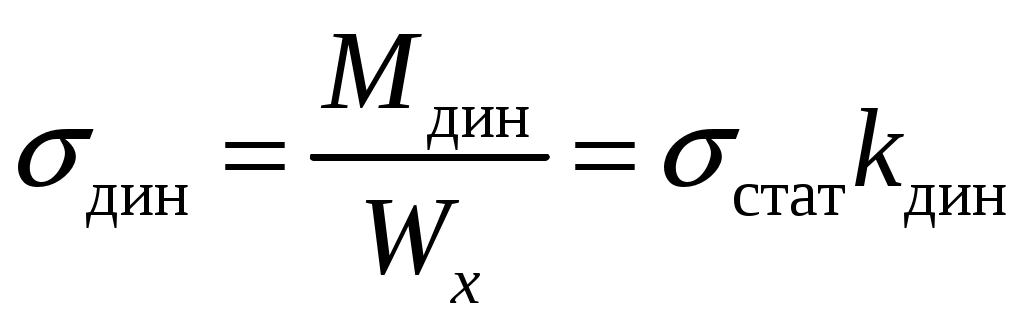 . .Определение перемещений и напряжений при ударе Рассмотрим случай продольного удара груза по неподвижному телу. Пусть груз весом q падает с высоты h на стержень. Скорость груза в момент удара определяется по известной формуле свободного падения Эта скорость за очень короткий промежуток времени удара, исчисляемый тысячными и сотыми долями секунды, упадет до нуля. Благодаря большой величине замедления возникает значительная сила инерции, величиной которой и определяется воздействие ударной нагрузки. Однако рассчитать закон изменения скорости во времени трудно, поэтому решение основывается на законе сохранения энергии. При расчете удара принимаются следующие допущения: Напряжения при ударе не превосходят предела пропорциональности, так что закон Гука сохраняет силу. Тела после удара не отделяются друг от друга. Масса ударяемого тела много меньше массы ударника, поэтому в расчет не принимается. Потерей части энергии, перешедшей в теплоту и в энергию колебательного движения, пренебрегаем. Работа, совершаемая весом падающего груза где  (a) Потенциальная энергия деформации основания где Р – контактное усилие. По закону Гука 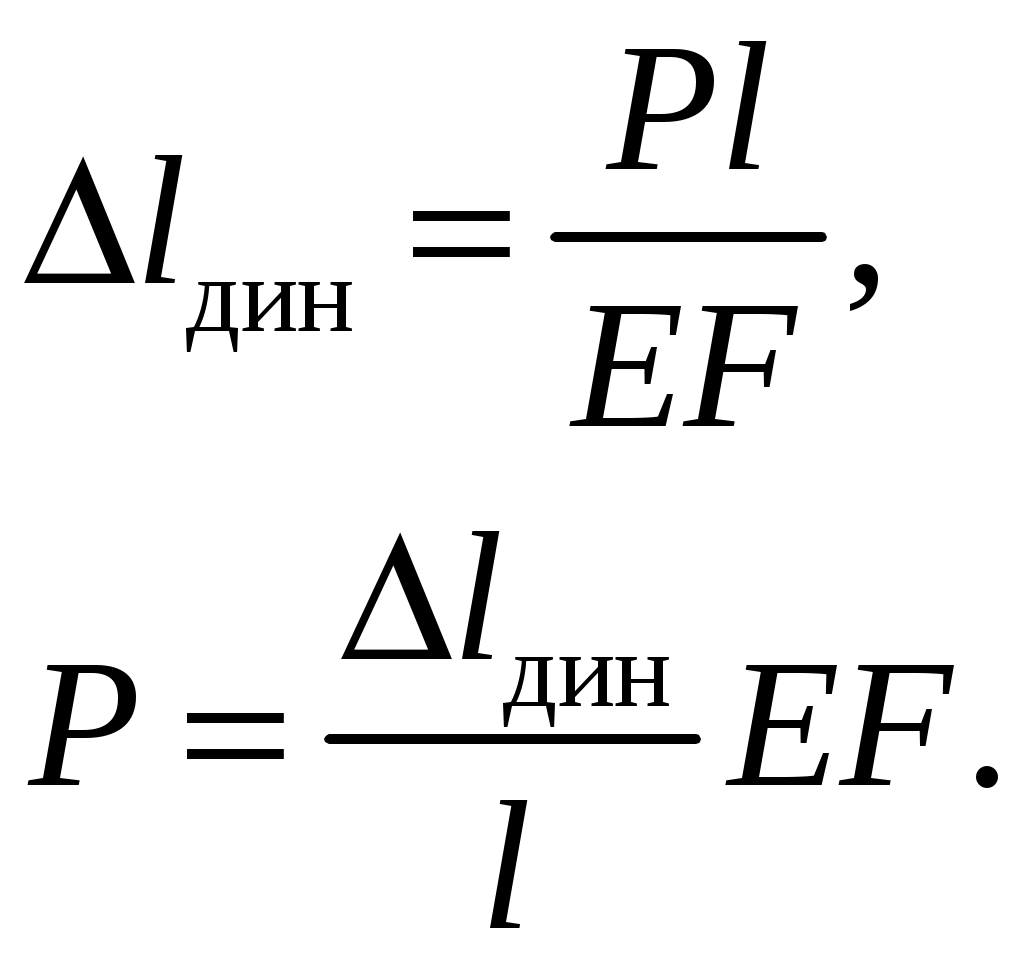 Подставляем выражение Р в (8.1) 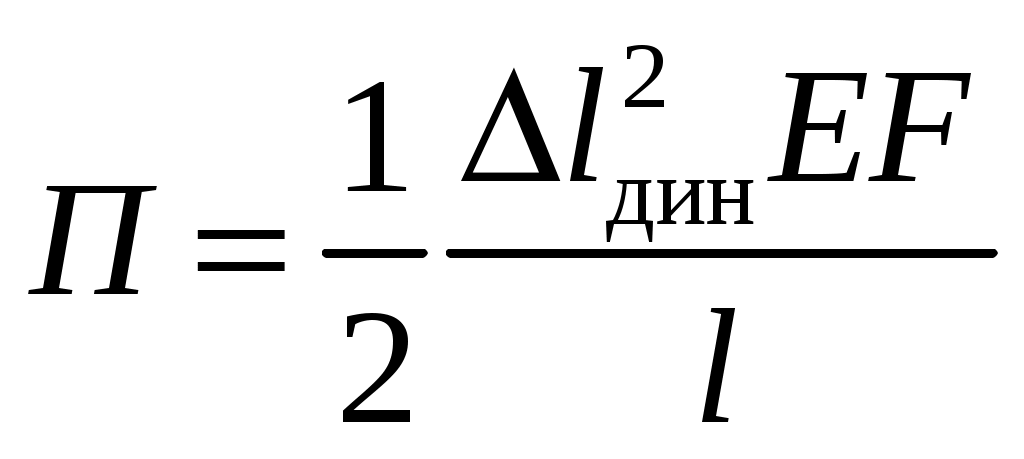 . .Считая, что работа падающего груза полностью переходит в потенциальную энергию сжатого основания, получаем 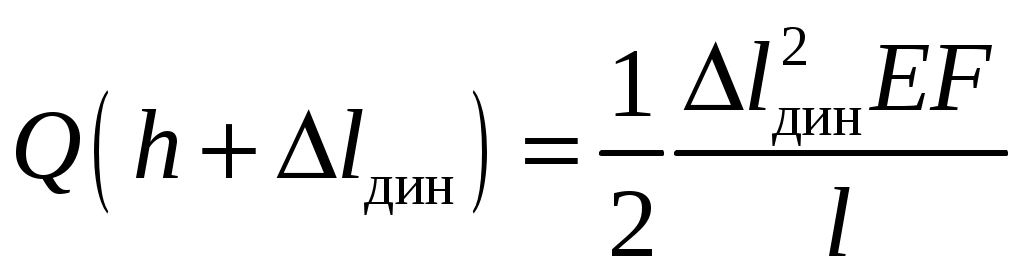 . (8.2) . (8.2)Выделим из (8.2) укорочение стержня от нагрузки Q, приложенной статически Тогда (8.2) преобразуется к виду Решая это квадратное уравнение относительно Выбираем знак плюс, поскольку перемещение от удара 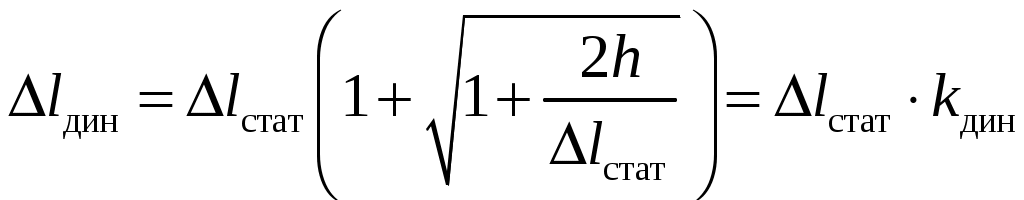 , (8.3) , (8.3)где Разделив обе части (8.3) на длину стержня l и умножив на модуль упругости E, перейдем, на основании закона Гука, от деформаций к напряжениям 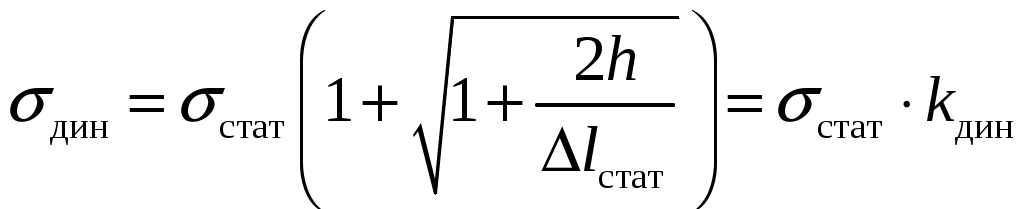 . (8.4) . (8.4)Из (8.3), (8.4) видно, что величины динамического напряжения и перемещения зависят от величины статической деформации ударяемого тела. Для смягчения удара применяют амортизирующие прокладки, дающие большие деформации и позволяющие, таким образом, расходовать энергию удара. Аналогичный вид имеют формулы и для случая поперечного удара по балке, только в этом случае вместо  . .Частные случаи 1. Если 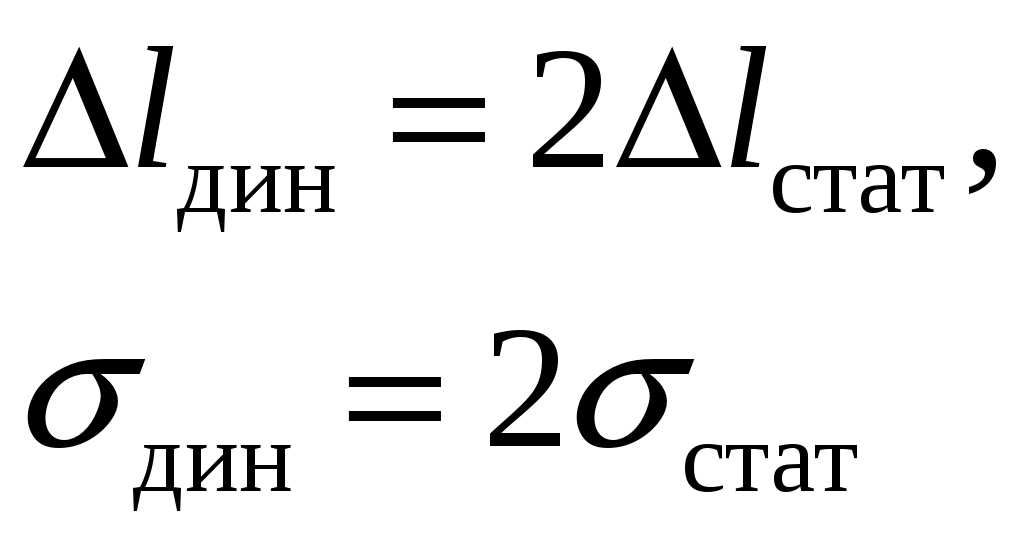 . .2. Если высота падения h много больше статической деформации 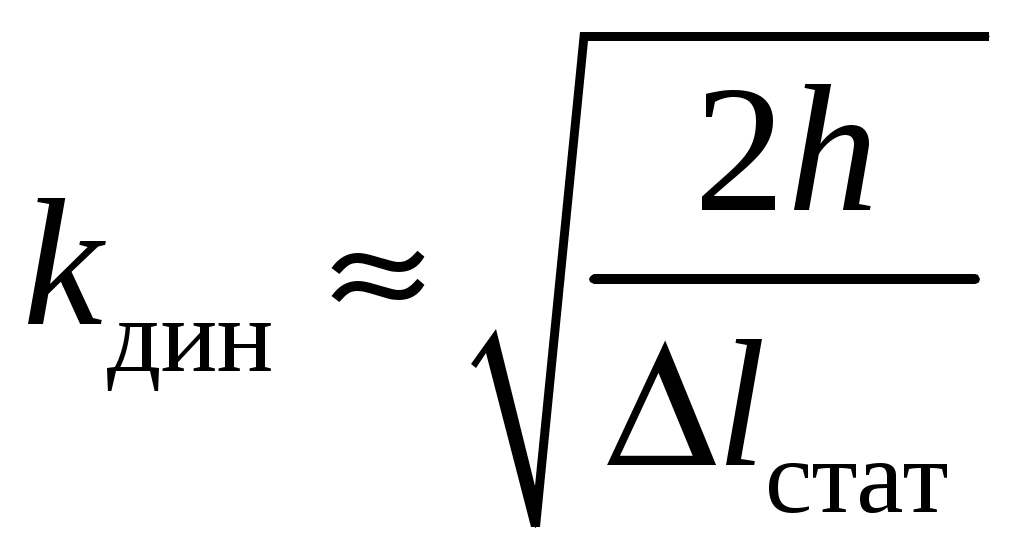 . .В некоторых случаях коэффициент динамичности удобно рассчитывать через скорость груза в момент удара 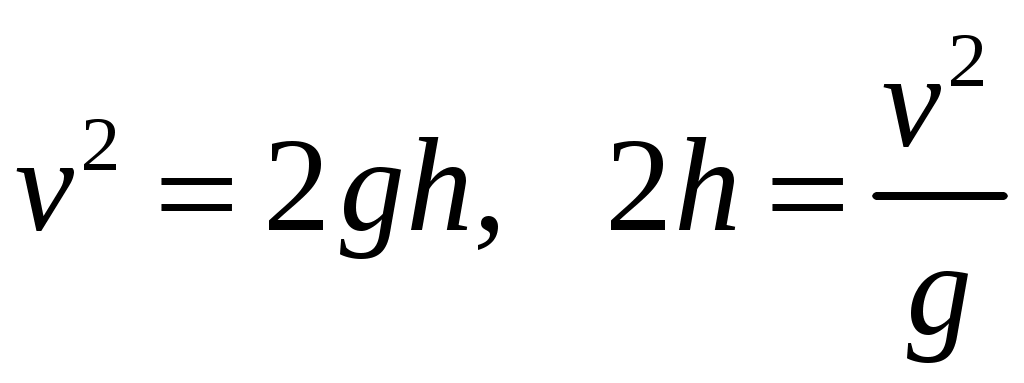 , ,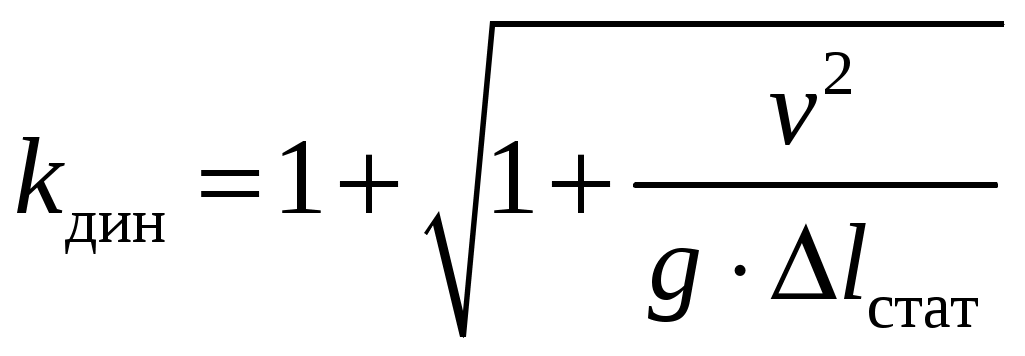 . .Колебания упругих систем Теория колебаний – раздел физики, охватывающий механику, электро-, радиотехнику, оптику. Особое значение теория колебаний имеет для прикладных задач прочности. Известно, что сооружения, рассчитанные с большим запасом на статическую прочность, разрушались от небольших периодически действующих сил. Колебания различают по числу степеней свободы. Число степеней свободы – это число независимых координат, определяющих положение системы. На рис. (а) приведена система с одной степенью свободы – координата ξ; на рис. (б) – система с тремя степенями свободы (две координаты центра тяжести тела с массой m и угол поворота). 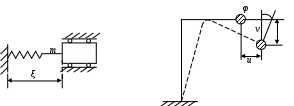 (а) (б) Число степеней свободы определяется выбором расчетной схемы, то есть степенью приближения, с которой мы считаем возможным исследовать реальный объект. Различают собственные (свободные) и вынужденные колебания. Собственные колебания – это колебания, совершаемые системой, освобожденной от внешних воздействий. Вынужденные колебания – колебания, совершаемые под действием изменяющихся со временем внешних сил. Период T собственных или вынужденных колебаний – промежуток времени между двумя смежными максимальными отклонениями от положения равновесия. Частота колебаний ν – величина, обратная периоду. Круговая частота (число колебаний за 2π секунд) Собственные колебания без затухания Динамическую модель упругой системы с одной степенью свободы представим в виде пружины с телом массой m на конце. В дальнейшем тело рассматривается как точечная масса. Степенью свободы является перемещение ξ, которое отсчитывается от ненапряженного состояния пружины. 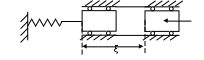 Исходя из принципа Даламбера, будем включать в уравнение статики силу инерции, направленную против перемещения и равную где 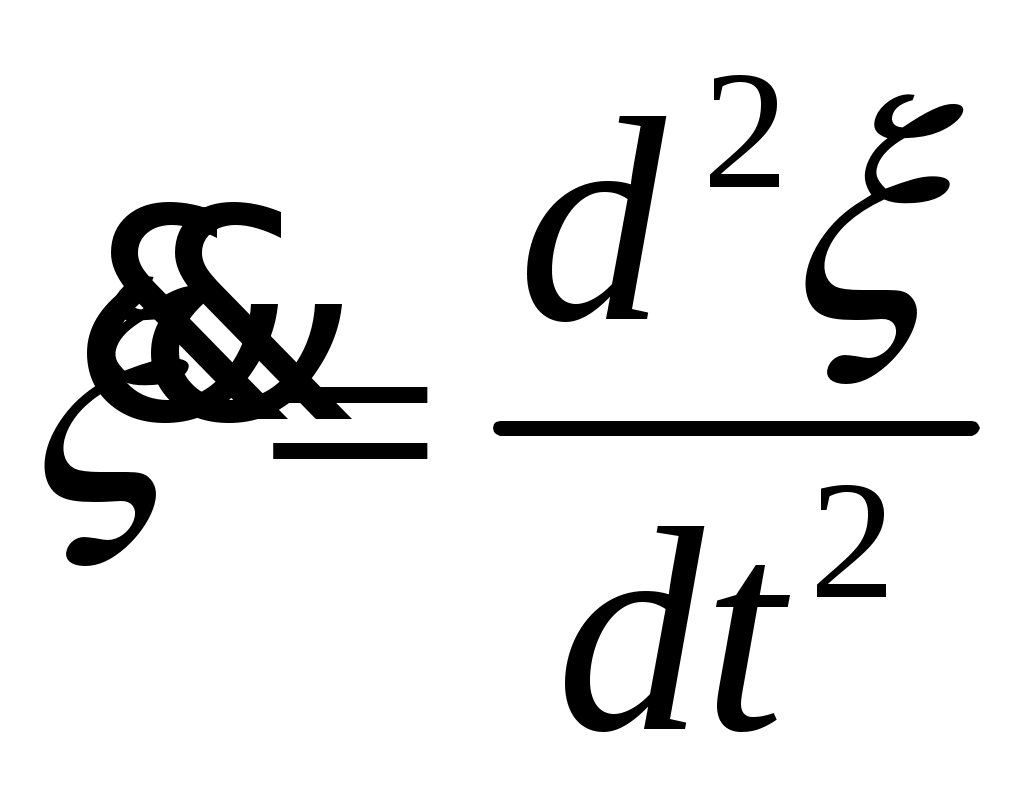 . .Перемещение ξ можно представить где 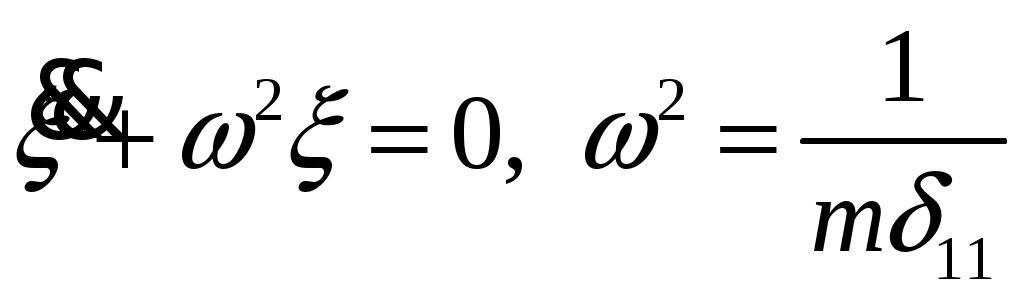 . (8.5) . (8.5)Решение (8.5) имеет вид Г 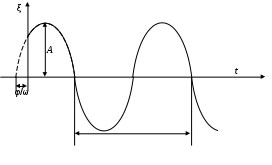 де С1, С2, А, φ – константы, определяемые из начальных условий при t= 0; А – амплитуда колебаний, φ – начальная фаза. График решения (8.6) имеет вид: де С1, С2, А, φ – константы, определяемые из начальных условий при t= 0; А – амплитуда колебаний, φ – начальная фаза. График решения (8.6) имеет вид:Собственные колебания с затуханием В предыдущем примере предполагалось, что собственные колебания происходят без рассеяния энергии (при отсутствии сил сопротивления), поэтому они могут длиться бесконечно долго. В реальных процессах всегда имеются внешние силы, уменьшающие амплитуду колебаний. Добавим силу сопротивлении к динамической модели упругой системы с одной степенью свободы. 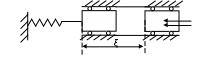 Закон сопротивления зададим в виде: где С учетом силы сопротивления имеем Отсюда получаем дифференциальное уравнение колебаний с затуханием 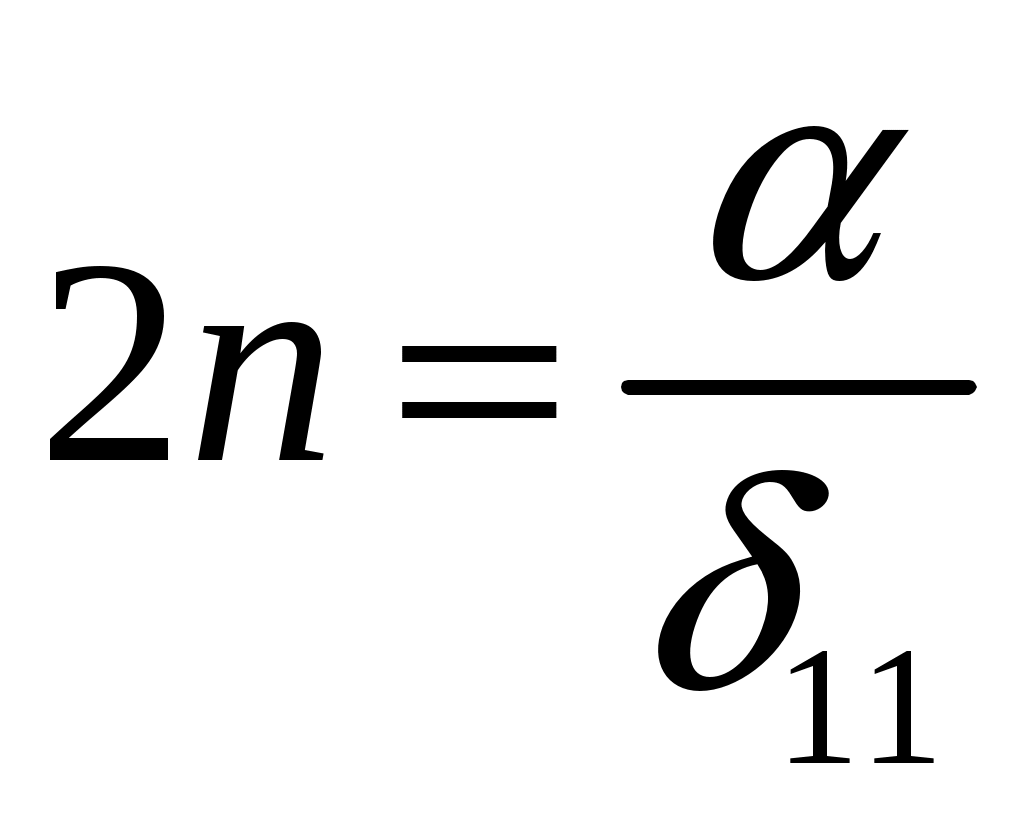 . .Решение (8.7) имеет вид: 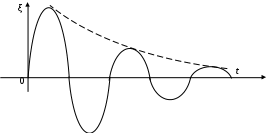 , (8.8) , (8.8)Где А, φ – константы, определяемые из двух начальных условий: где Графически решение (8.8) представляет собой затухающую синусоиду. Через интервал 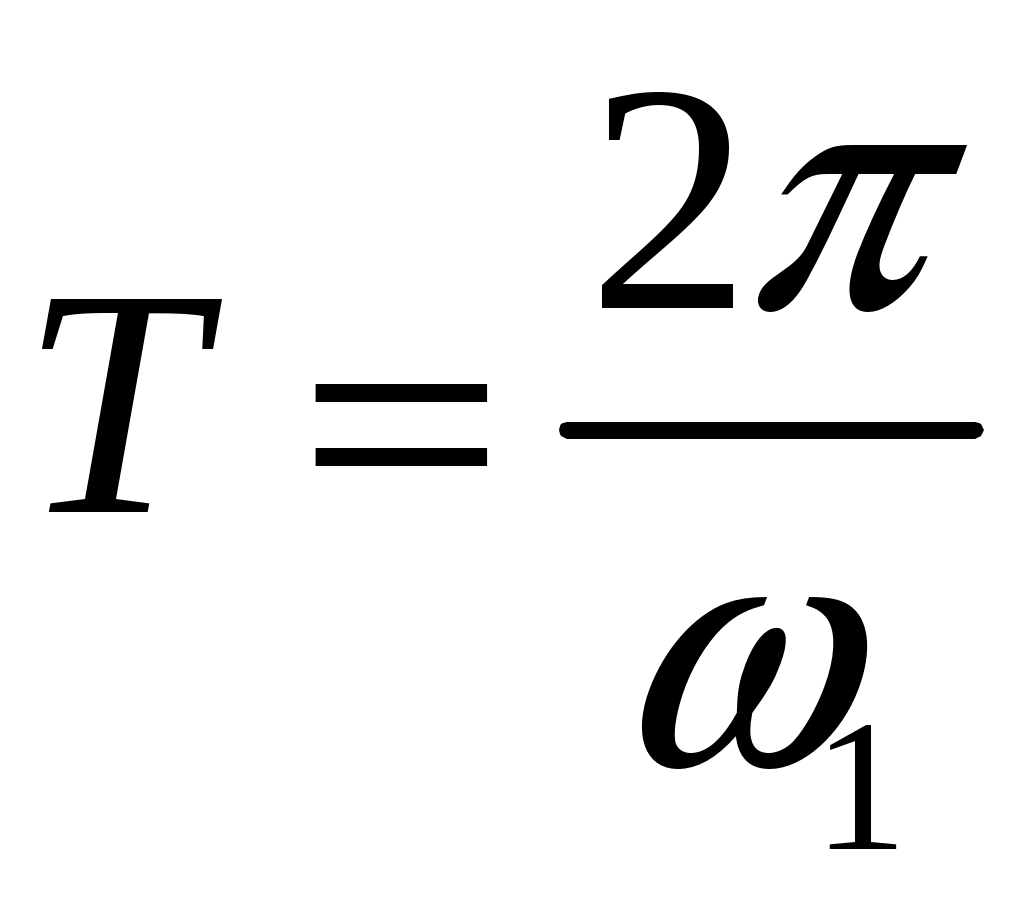 амплитуда согласно (8.8) уменьшится в амплитуда согласно (8.8) уменьшится в 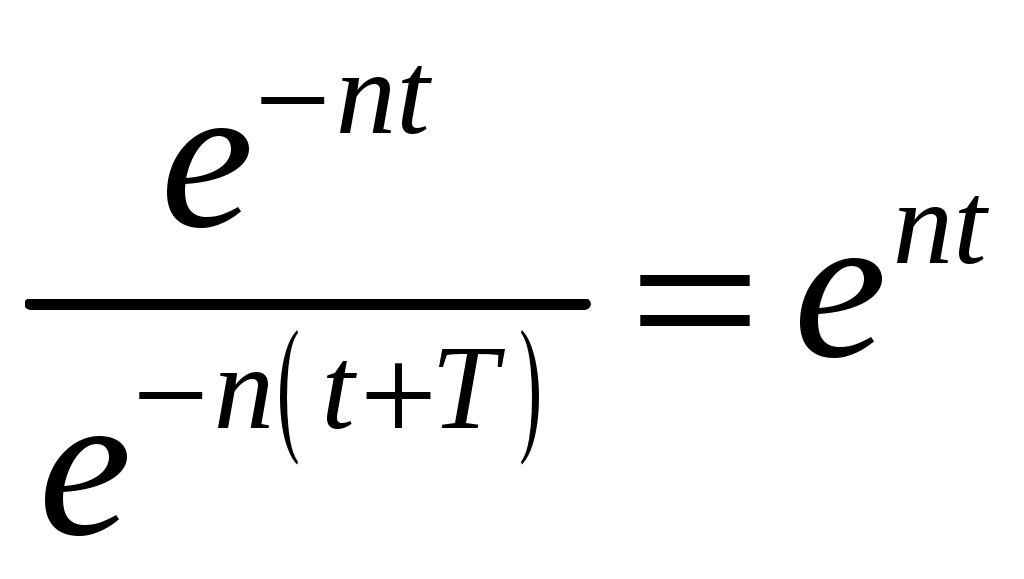 . .Величина nT называется декрементом затухания. Вынужденные колебания. Резонанс Пусть на систему с одной степенью свободы действует вынужденная (внешняя) сила, изменяющаяся во времени по закону Дифференциальное уравнение вынужденных колебаний без учета сил сопротивления имеет вид: По сравнению с уравнением свободных колебаний (8.5) здесь мы имеем неоднородное уравнение с правой частью, зависящей от времени. Решение (8.9) будем искать в виде суммы общего решения однородного уравнения плюс частное решение неоднородного где Частное решение неоднородного уравнения (8.9) возьмем в виде: Простой подстановкой в (8.9) можно убедиться, что решение в виде (8.10) справедливо, если 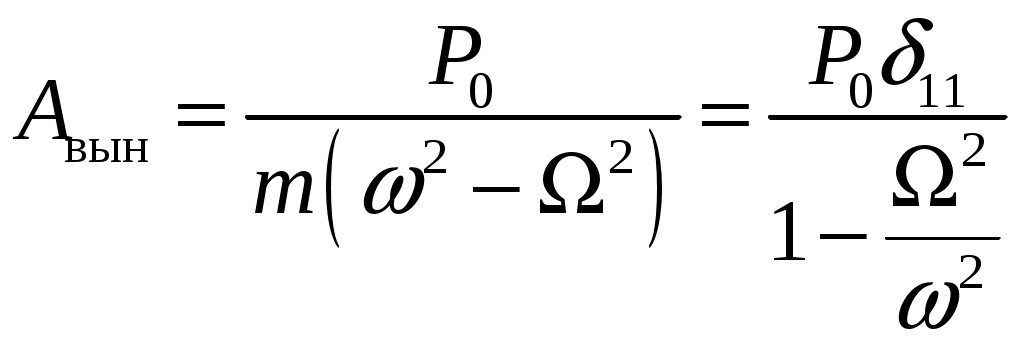 . .Общее решение уравнения (8.9) тогда будет 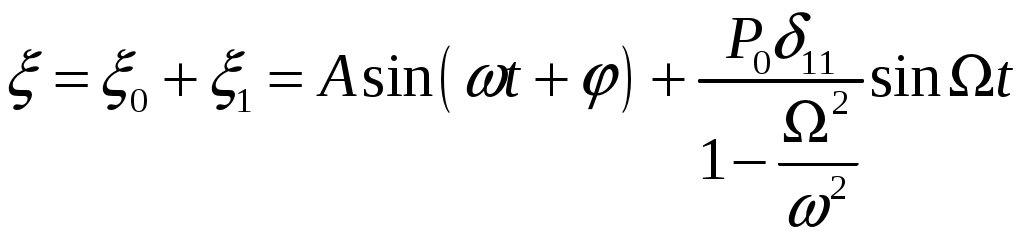 . (8.11) . (8.11)Свободные колебания, представленные в (8.11) первым слагаемым, со временем затухают. Вынужденные происходят с частотой вынуждающей силы где 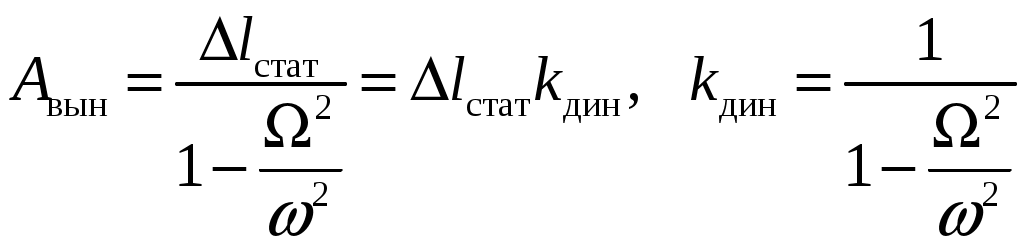 . .К 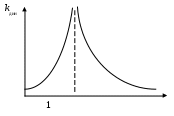 оэффициент динамичности показывает, во сколько раз амплитуда вынужденных колебаний больше статического перемещения. оэффициент динамичности показывает, во сколько раз амплитуда вынужденных колебаний больше статического перемещения.При В действительности, если учесть влияние сил сопротивления, увеличение амплитуды будет конечно, хотя и достаточно большим. Явление повышения амплитуды при совпадении частоты собственных колебаний и частоты изменения возмущающей силы называется |
