Введение 1 Наука о сопротивлении материалов
 Скачать 4.19 Mb.
|
|
резонансом. При расчете на прочность динамических конструкций явлению резонанса уделяется первостепенное внимание. Значительное увеличение амплитуды колебаний может привести к разрушению даже при небольшой разрушающей силе. Для предотвращения резонанса существуют два конструктивных подхода. 1. При проектировании конструкций следует добиваться того, чтобы собственная частота колебаний системы значительно отличалась от частоты  изменения вынуждающей силы.2. Уменьшить колебания при резонансе можно за счет увеличения коэффициента затухания  , то есть за счет повышения рассеивания энергии.9. Продольный изгиб (устойчивость сжатых стержней) Устойчивость – свойство элемента сохранять начальную форму равновесия при внешних воздействиях. Проблема возникновения устойчивости возникает при осевом сжатии стержня, размеры поперечного сечения которого малы по сравнению с длиной. При увеличении сжимающей нагрузки начальная (прямолинейная) форма равновесия теряется и ось стержня искривляется. Величина сжимающей силы, при которой происходит потеря устойчивости стержня, называется критической силой Pкр.  (а) Для балки, изображенной на рисунке, при  балка испытывает только сжатие, при  - сжатие с изгибом. С точки зрения расчетов на устойчивость, значение  должно рассматриваться как критическая нагрузка.В целях безопасности допускаемая нагрузка должна быть меньше критической: 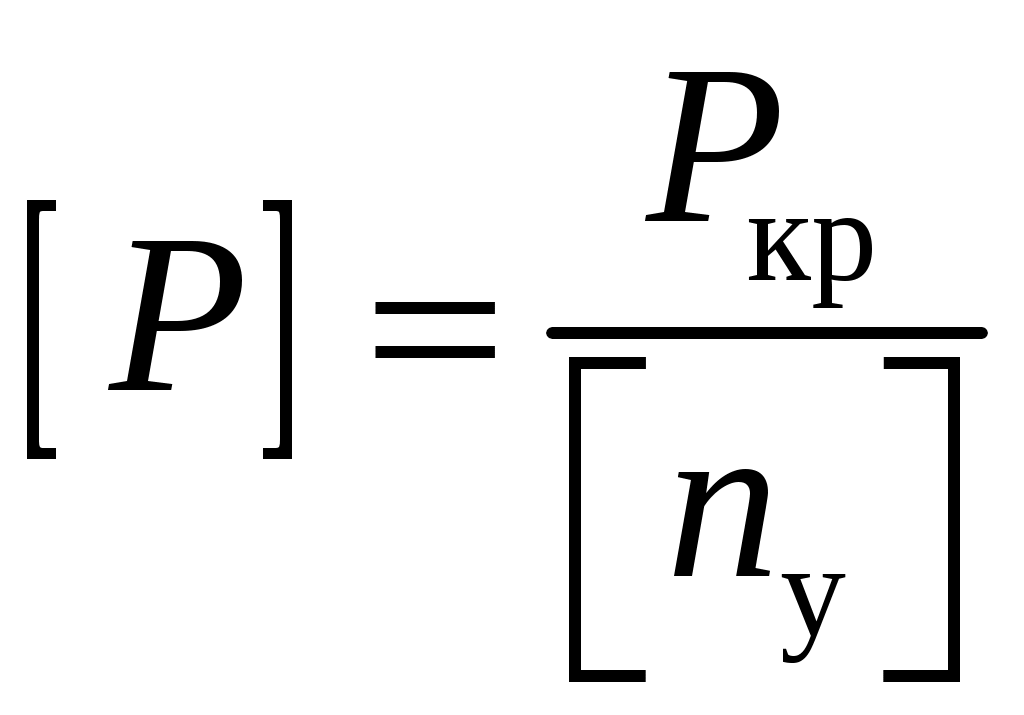 ,где  - коэффициент запаса устойчивости. Для стали величина принимается в пределах 1,8÷3, для чугуна – 5÷5,5, для дерева – 2,8÷3,2.Задача Эйлера определения критической силы Для балки, изображенной на рисунке (а), проведем сечение на расстоянии z и рассмотрим равновесие изогнутой части 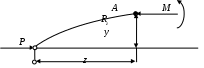 Здесь Rz = P – равнодействующая внутренних сил. Сумма моментов относительно поперечной оси сечения   .Поскольку изгибающий момент в сечении связан с прогибом  дифференциальным уравнением , то получаем  .Обозначим  , тогда получим уравнение Эйлера . (9.1)Общее решение (9.1) имеет вид:  . (9.2)Константы a, b определяются из граничных условий   .  .Последнее уравнение имеет два решения:  и  . Случай дает согласно найденному  и решению (9.2) нулевое значение  . Этот случай соответствует условию отсутствия прогибов балки и, следовательно, процессу сжатия стержня без изгиба. Поскольку нас интересует определение критической силы при потере устойчивости, то рассмотрим второе решение:  Далее получаем 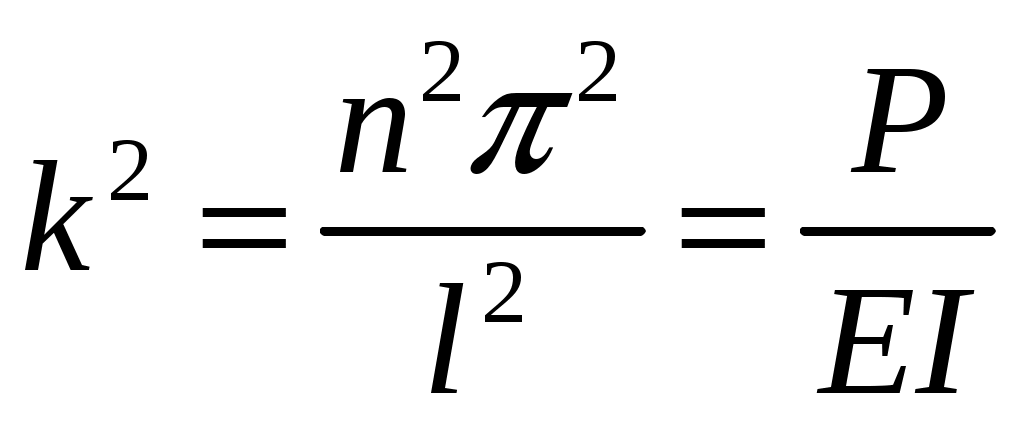 .Отсюда находим значение критической силы 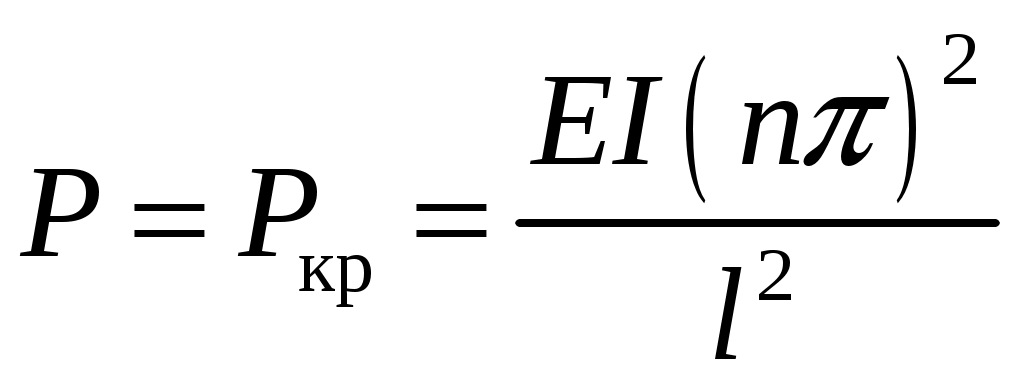 . (9.3)Критическая сила пропорциональна жесткости стержня на изгиб и обратно пропорциональна квадрату длины стержня. Относительно выбора момента инерции в решении (9.3) заметим следующее. Если моменты инерции относительно двух главных центральных осей инерции поперечного сечения не равны между собой, то продольный изгиб произойдет в плоскости наименьшей жесткости, то есть поперечные сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение. Следовательно, вместо I нужно использовать Imin. С практической точки зрения интерес представляет наименьшее значение критической силы, при которой происходит потеря устойчивости. При n = 1 в (9.3) получаем 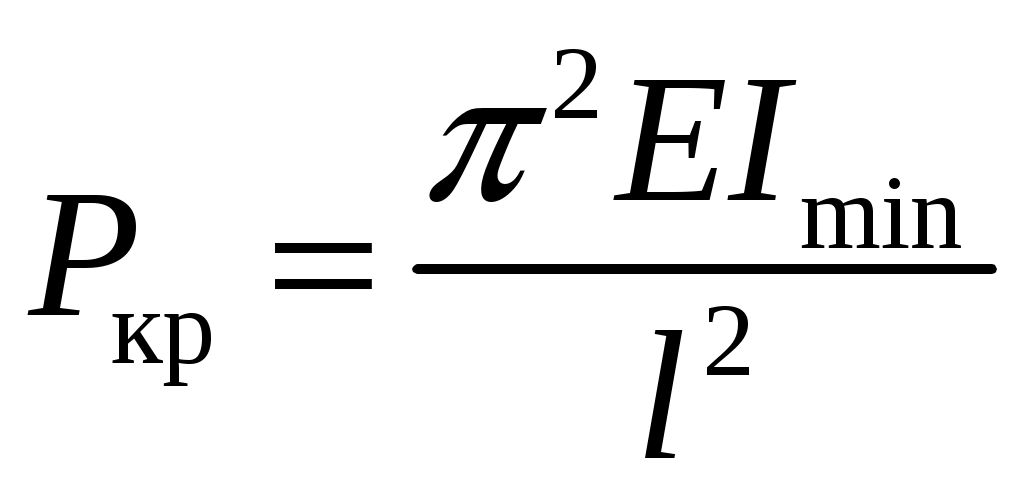 .Влияние способов закрепления стержня Ч 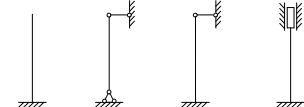 аще всего концы стержня закрепляют одним из четырех способов, показанных на рисунке.Второй способ – шарнирное закрепление концов – рассмотрен в решении Эйлера. При других способах закрепления используется обобщенная формула Эйлера 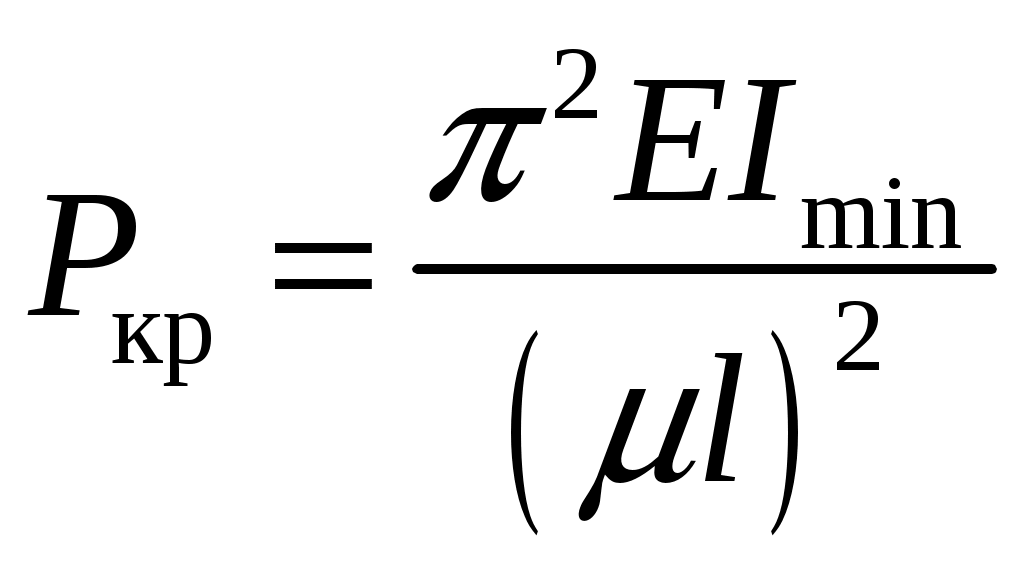 . (9.4)где  - коэффициент приведения длины стержня.Значения коэффициента при других способах закрепления приведены в литературе.Предел применимости формулы Эйлера Значение критического напряжения на основе (9.4) будет 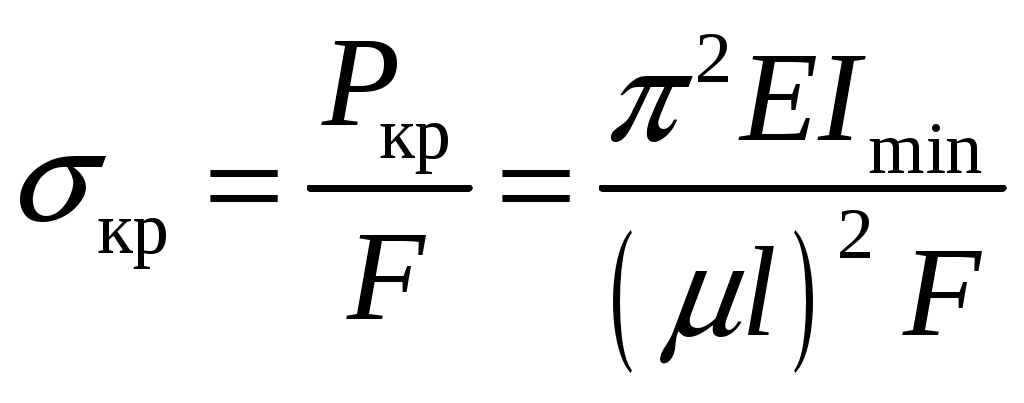 .Введем радиус инерции сечения  .Тогда 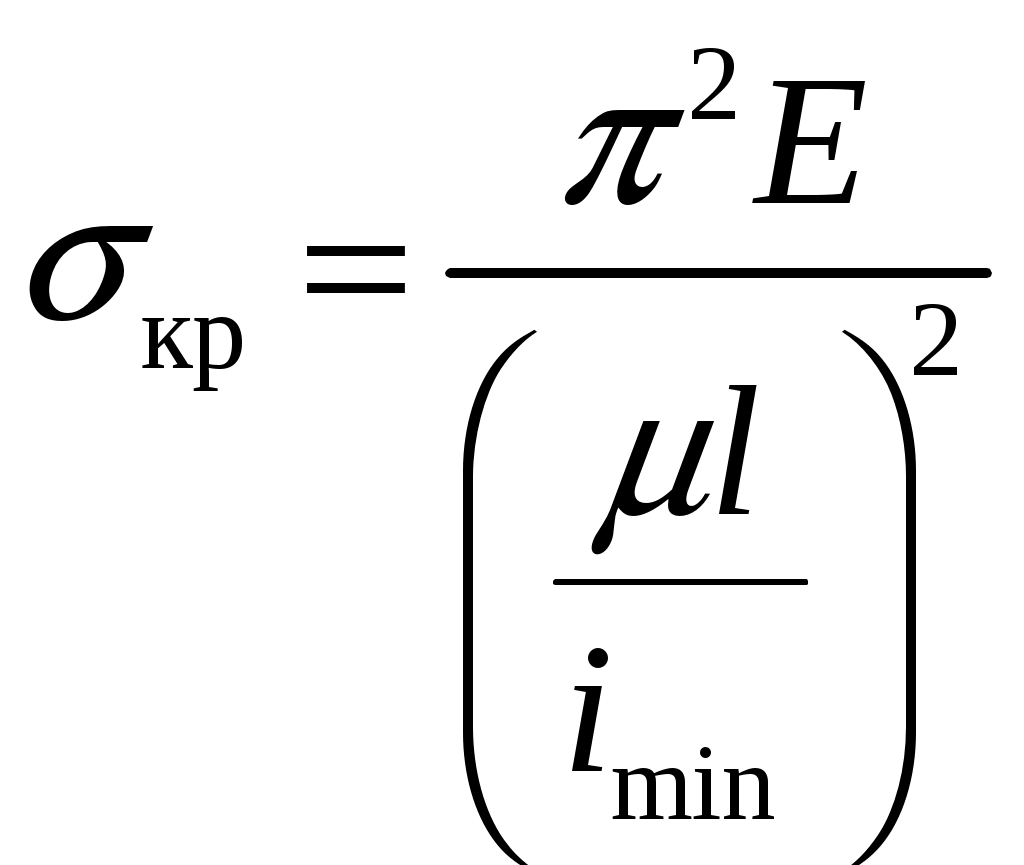 .Обозначим величину, стоящую в круглых скобках, через 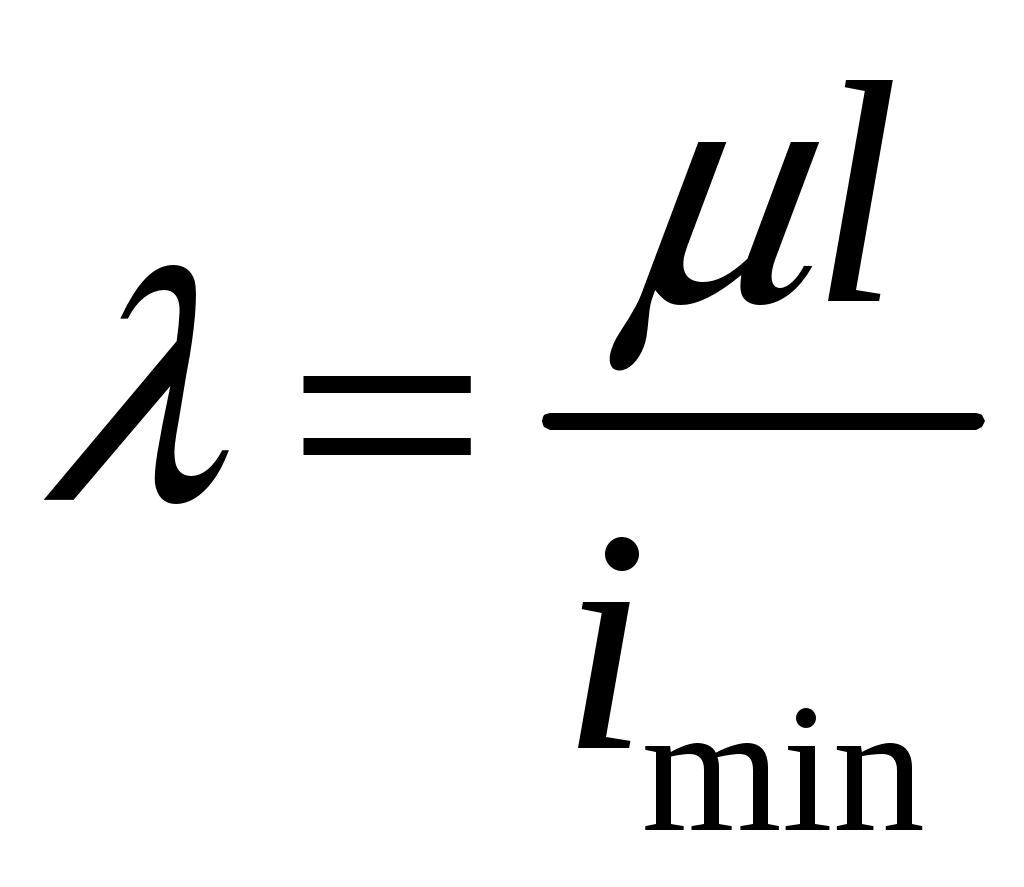 и назовем ее гибкостью стержня .Критическое напряжение определится как 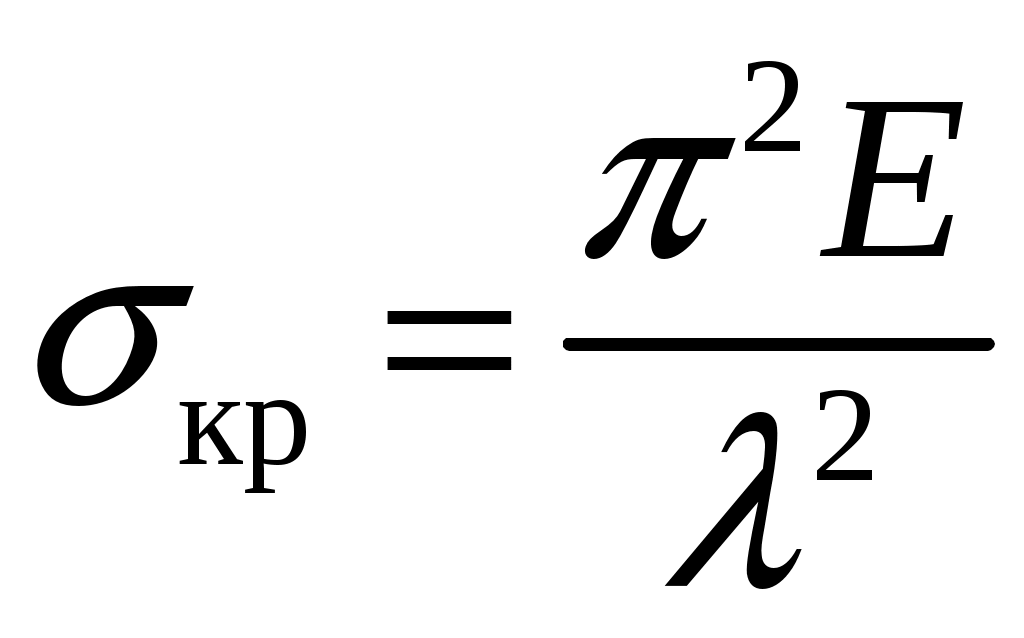 . (9.5)При выводе решения Эйлера мы пользовались дифференциальным уравнением упругой линии, которое справедливо, если материал работает в пределах выполнимости закона Гука, когда напряжения не превосходят предела пропорциональности 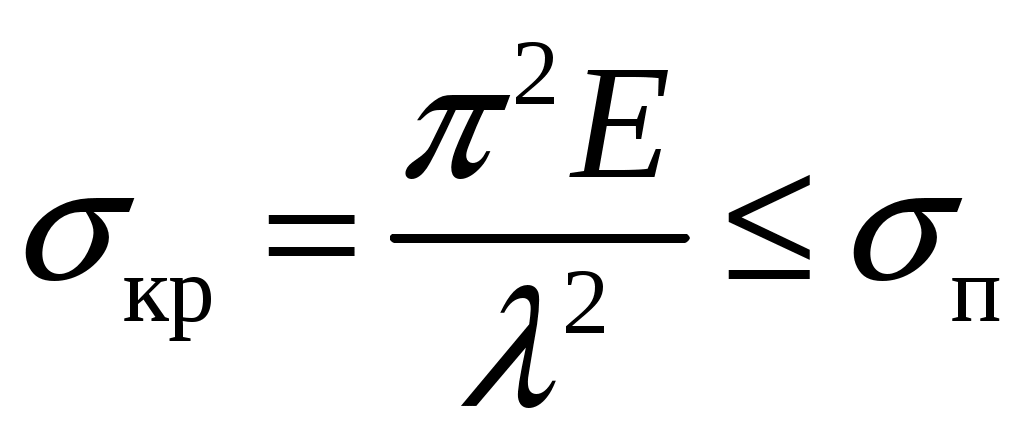 . Следовательно, условием применимости решения Эйлера будет  .Отсюда находим соответствующее предельное значение гибкости 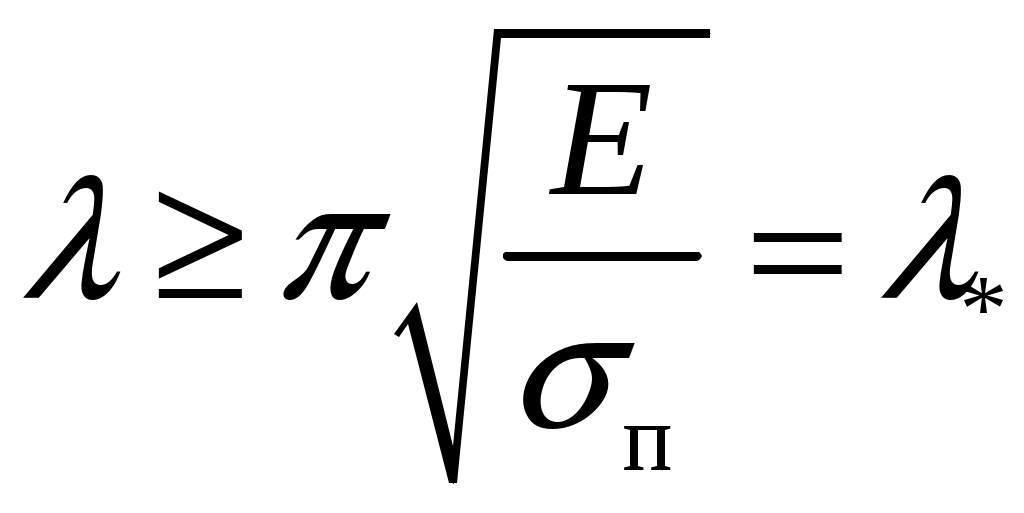  .Для стали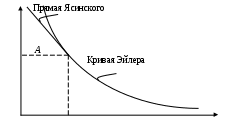: = 2000 кг/см2, E = 2·106 кг/см2,  = 100.З  ависимость критического напряжения от гибкости можно представить графическиТочка A соответствует предельным значениям ( , ). При  ,  решение (9.5) не имеет смысла.Метод расчета критической силы при малой гибкости за пределами упругого поведения был найден Ясинским опытным путем. Согласно формуле Ясинского, при зависимость  от представима линейной функцией .Константы a, b при  для стали: a = 3100 кг/см2, b = 3100 кг/см2/При гибкости  стержни можно рассчитывать на прочность без учета опасности продольного изгиба.Практическая формула расчета на устойчивость Вместо двух формул (Эйлера и Ясинского), каждая из которых справедлива для определенного диапазона гибкостей, удобно иметь практическую формулу, которой можно было бы пользоваться при любой гибкости стержня. Данная формула имеет вид  . (9.6)где  - допускаемое напряжение на сжатие; - коэффициент уменьшения допускаемого напряжения, зависящий от свойств материала и гибкости стержня. Его значения приведены в таблицах.Для подбора сечения F формулу (9.6) приводят к виду: 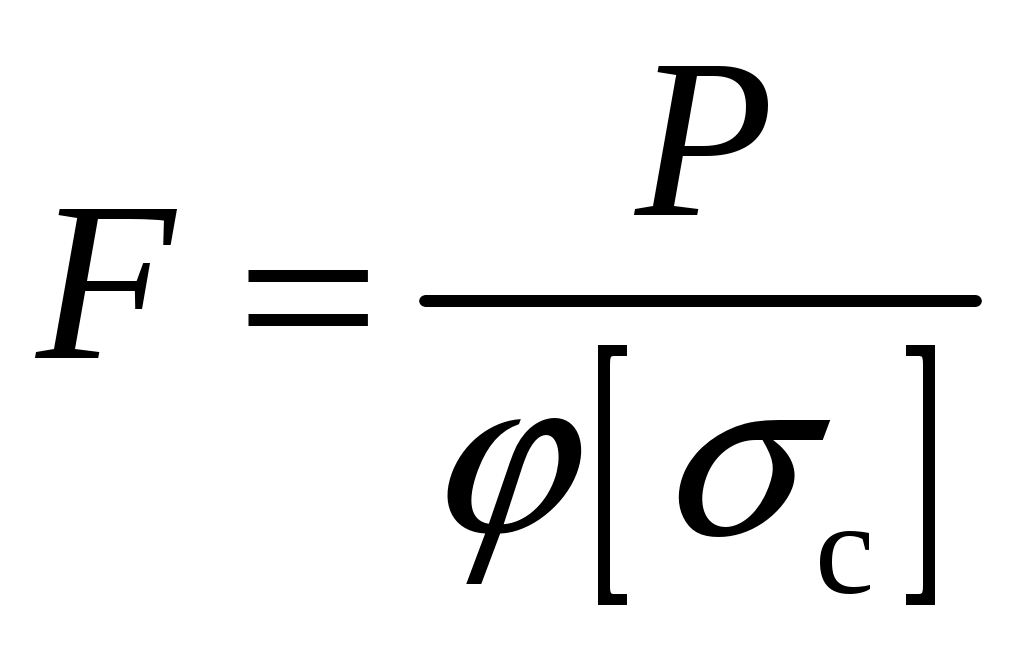 .При этом величина P должна быть известна, а величиной необходимо задаваться, поскольку гибкость неизвестна, ибо неизвестна величина площади сечения F. В качестве первого приближения в целях построения сходящейся итерационной процедуры отыскания F рекомендуется задать  . Затем определяют  и по таблице находят  , соответствующее  . Если разница между  и превышает 5%, то следует повторить расчет, задавшись  .Рациональные формы сечений На уровень критических напряжений существенное влияние оказывает гибкость , величина которой зависит от минимального радиуса инерции  . При выборе формы сечения желательно стремиться к максимально возможной величине при определенной площади F. Это обеспечивает минимальный расход материала.Введем удельный радиус инерции сечения 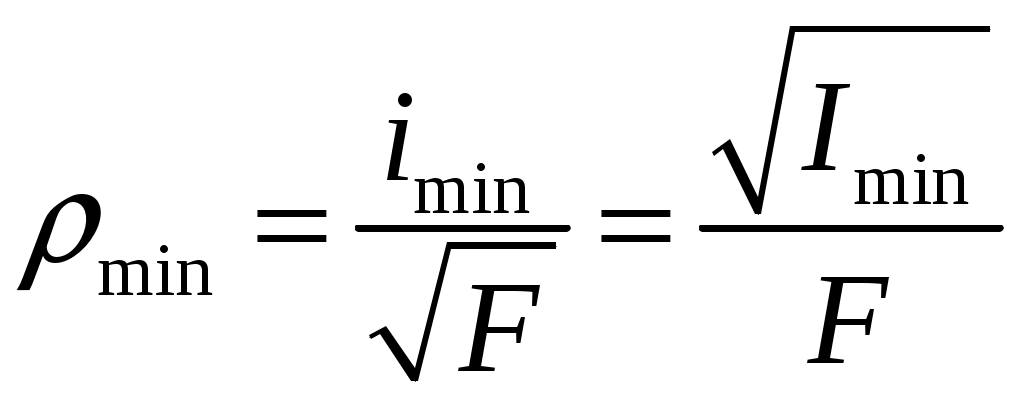 .Чем больше величина  , тем более рациональным является сечение. Для этого необходимо обеспечить периферийное расположение материала по сечению. Значения параметра приведены в таблице 1.Таблица 1
|
)