Введение 1 Наука о сопротивлении материалов
 Скачать 4.19 Mb.
|
1.8 Перемещения и деформацииПод действием внешних сил, происходит изменение геометрической формы рассматриваемого тела, при этом различные точки тела неодинаково перемещаются в пространстве. Рассмотрим точки А и В материального тела в недеформированном состоянии. Расстояние между точками l (рис. 1.13). Под действием внешних сил форма тела изменилась, и рассматриваемые точки оказались в положении А1В1. Расстояние между ними изменилось А1В1 = (l+Δl). 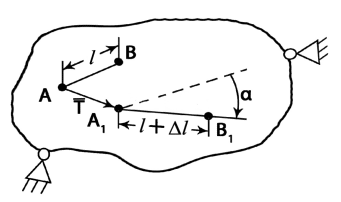 Рис.1.13 Величина  характеризует линейную деформацию, и называется относительным удлинением.Вектор  , имеющий своё начало в точке А недеформированного состояния, а конец в точке А1 деформированного состояния характеризует линейное перемещение точки А.Если за исходное состояние принять положение АВ, то угол α характеризует угловое перемещение отрезка АВ (поворот) (рис.1.14). 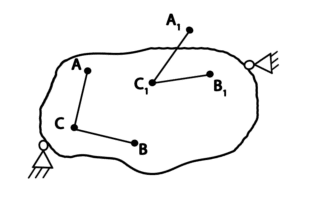 Рис.1.14 Угловая деформация характеризуется изменением угла, образованного двумя отрезками АС и ВС, взаимно перпендикулярными в недеформированном состоянии. Вследствие деформации отрезки занимают положение А1С1 и В1С1. Величина  характеризует угловую деформацию, или сдвиг.Лекция 2 Растяжение, сжатие Определение внутренних усилий Растяжение (сжатие) имеет место в том случае, когда внешние усилия действуют строго вдоль центральной оси стержня в противоположные стороны ( рис. 2.1,а ; 2.1,в) .  а) б) в ) Рис.2.1 Именно при таком нагружении в поперечном сечении стержня действует только нормальное внутреннее усилие N, − все прочие равны нулю. На растяжение, сжатие работают тросы, канаты, стержни ферм, колонны, штанги бурового инструмента. Внутренние усилия определяют методом сечений и вычисляют исходя из условий равновесия. Проводим мысленно сечение mn и отбрасываем любую из частей стержня, заменяя её действие на оставшуюся силой N( рис 2.1,б). Рассматриваемая часть стержня работает на растяжение. Записываем условие равновесия рассматриваемой части  , откуда следует, что N= P, направлена вдоль оси стержня от сечения. Очевидно, что внутренне усилие, направленное к сечению будет означать сжатие.В том случае, когда на стержень действует система сил (рис. 2.2а) внутреннее усилие в любом сечении равно алгебраической сумме внешних сил, расположенных по одну сторону от рассматриваемого сечения. 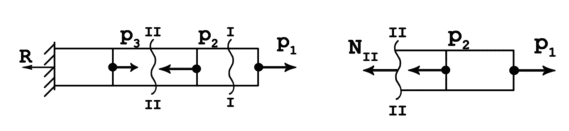 а) б) Рис. 2.2 Запишем условие равновесия правой части стержня, отсечённой сечением II (рис. 2.2,б)  , от куда  . Знак «+» при решении говорит о том, что внутреннее усилие направлено верно, знак «-» указывает на то, что внутреннее усилие следует направить в противоположную сторону.2.2 Напряжение в поперечных сечениях растянутого стержняЭкспериментальное наблюдение показывает, что, если на поверхность растягиваемого образца нанести сетку из продольных и поперечных линий (рис. 2.3а), то после нагружения поперечные линии остаются прямолинейными и параллельными друг другу; меняется лишь расстояние между ними. 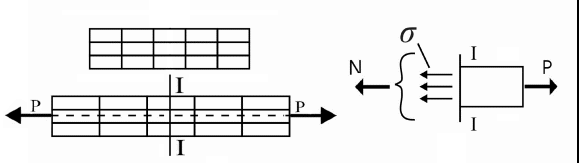 а) б) Рис.2.3 Это означает, что внутреннее усилие N равномерно распределено по поперечному сечению. Величина внутреннего усилия, приходящаяся на единицу сечения, есть напряжение. При растяжении, сжатии имеют место нормальные усилия N, а, следовательно, и нормальные напряжения  (2.1)Здесь А − площадь поперечного сечения. Прочность при любом виде нагружения сохраняется до тех пор, пока действующее максимальное напряжение не превзойдёт некоторой величины, безопасной для этого материала  . (2.2)Здесь σmax − действующее напряжение, [σ] − допускаемое напряжение, определяемое экспериментально. Условие прочности при растяжении, сжатии имеет вид:  (2.3)Значения допускаемых напряжений Таблица2.1
Исходя из условия прочности можно решить три типа задач: Проверка прочности существующей конструкции (2.4) Определение площади поперечного сечения, обеспечивающего прочность 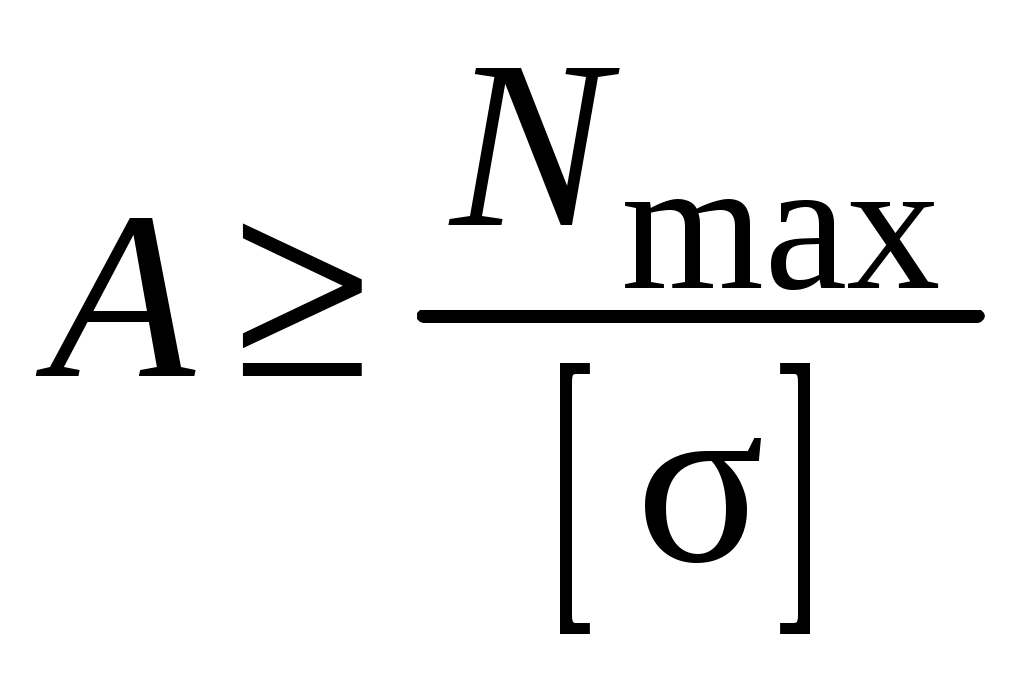 (2.5)Размеры поперечного сечения определяют, исходя из его формы. Определение грузоподъёмности системы  (2.6)Наибольшее допускаемое внутреннее усилие в конструкции позволяет определить допускаемую внешнюю нагрузку. Пример 1. Определить наибольший вес груза G для симметричной системы (рис 2.4а), состоящей из двух стрежней. Дано: l1 = l2 = l; α; [σ]; A1 = A2 = A. 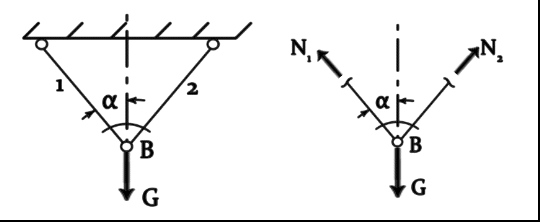 а) б) Рис.2.4 Определяем внутренние усилия N1 и N2, возникающие в стрежнях в результате действия груза. Пользуясь методом сечений, вырезаем узел В и записываем условия равновесия отсечённой части. 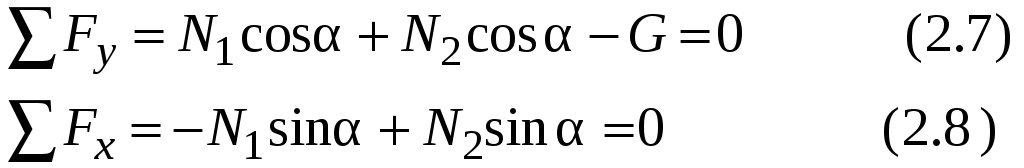 Из уравнения 2.7 следует, что в стержнях развиваются равные усилия N1 = N2 = N. Подставляя полученное в уравнение 2.8, имеем  Допускаемое усилие для 1 и 2 стержней – [N] = [σ]A. Таким образом  |